Introduction to Medical Imaging rotate source-detector pair around - PowerPoint PPT Presentation

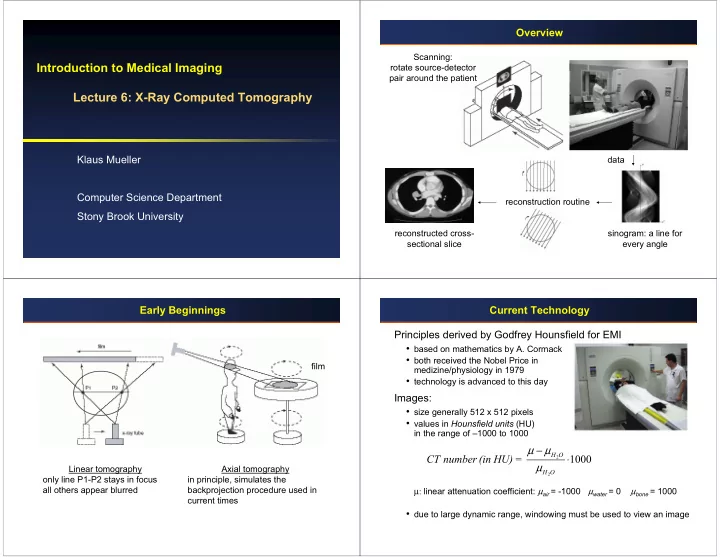
Overview Scanning: Introduction to Medical Imaging rotate source-detector pair around the patient Lecture 6: X-Ray Computed Tomography Klaus Mueller data Computer Science Department reconstruction routine Stony Brook University reconstructed cross- sinogram: a line for sectional slice every angle Early Beginnings Current Technology Principles derived by Godfrey Hounsfield for EMI • based on mathematics by A. Cormack • both received the Nobel Price in film medizine/physiology in 1979 • technology is advanced to this day Images: • size generally 512 x 512 pixels • values in Hounsfield units (HU) in the range of –1000 to 1000 µ − µ H O CT number (in HU) = 1000 2 ⋅ µ Linear tomography Axial tomography H O 2 only line P1-P2 stays in focus in principle, simulates the all others appear blurred backprojection procedure used in µ: linear attenuation coefficient: µ air = -1000 µ water = 0 µ bone = 1000 current times • due to large dynamic range, windowing must be used to view an image

CT Detectors Projection Coordinate System The parallel-beam geometry at angle θ represents a new Scintillation crystal with photomultiplier tube (PMT) coordinate system ( r , s ) in which projection I θ ( r ) is acquired (scintillator: material that converts ionizing radiation into pulses of light) • rotation matrix R transforms coordinate system ( x, y ) to ( r, s ): • high QE and response time • low packing density ⎛ ⎞ ⎛ ⎞ ⎛ ⎞⎛ ⎞ r x cos sin x θ θ • PMT used only in the early CT scanners R ⎜ ⎟ = ⎜ ⎟ = ⎜ ⎟⎜ ⎟ s y sin cos y ⎝ ⎠ ⎝ ⎠ ⎝ − θ θ ⎠⎝ ⎠ Gas ionization chambers that is, all ( x , y ) points that fulfill • replace PMT r = x cos( θ ) + y sin( θ ) • X-rays cause ionization of gas molecules in chamber are on the (ray) line L (r, θ ) • ionization results in free electrons/ions • R T is the inverse, mapping • these drift to anode/cathode and yield a measurable electric signal ( r, s ) to ( x, y ) • lower QE and response time than PMT systems, but higher packing ⎛ x ⎞ ⎛ ⎞ r ⎛ cos sin ⎞⎛ ⎞ r θ − θ density T R ⎜ ⎟ = ⎜ ⎟ = ⎜ ⎟⎜ ⎟ y s sin cos s ⎝ ⎠ ⎝ ⎠ ⎝ θ θ ⎠⎝ ⎠ Scintillation crystals with photodiode • current technology (based on solid state or semiconductors) s is the parametric variable • photodiodes convert scintillations into measurable electric current along the (ray) line L (r, θ ) • QE > 98% and very fast response time Projection Projection Profile Assuming a fixed angle θ , the measured intensity at detector Each intensity profile I θ ( r ) is transformed to into an attenuation position r is the integrated density along L (r, θ ) : profile p θ ( r ): ∫ ( , ) x y ds I ( ) r − µ ∫ p r ( ) ln ( r cos s sin , r sin s cos ) ds θ = − = µ ⋅ θ − ⋅ θ ⋅ θ + ⋅ θ I ( ) r I e Lr = ⋅ , θ θ I 0 θ 0 L ∫ r , θ ( cos r s sin , sin r s cos ) ds − µ ⋅ θ − ⋅ θ ⋅ θ + ⋅ θ I e Lr = ⋅ , θ I θ ( r ) p θ ( r ) 0 For a continuous energy spectrum: ∫ ( cos r s sin , sin r s cos ) ds − µ ⋅ θ − ⋅ θ ⋅ θ + ⋅ θ ∞ ∫ I ( ) r I ( ) E e Lr = ⋅ , θ 0 θ 0 • p θ ( r ) is zero for | r |> FOV /2 ( FOV = F ield o f V iew, detector width) But in practice, is is assumed that the • p θ ( r ) can be measured from (0, 2 π ) X-rays are monochromatic • however, for parallel beam views ( π , 2 π ) are redundant, so just need to measure from (0, π )

Sinogram Radon Transform Stacking all projections (line integrals) yields The transformation of any function f ( x , y ) into p ( r , θ ) is called the sinogram, a 2D dataset p ( r , θ ) the Radon Transform p r ( , ) R f x y { ( , )} θ = ∞ ∫ f r ( cos s sin , r sin s cos ) ds = ⋅ θ − ⋅ θ ⋅ θ + ⋅ θ To illustrate, imagine an object that is −∞ a single point: The Radon transform has the following properties: • it then describes a sinusoid in p ( r , θ ): • p ( r , θ ) is periodic in θ with period 2 π p r ( , ) p r ( , 2 ) θ = θ + π • p ( r , θ ) is symmetric in θ with period π p r ( , ) p ( r , ) θ = − θ ± π projections point object sinogram Sampling (1) Sampling (2) spatial domain frequency domain In practice, we only have a limited • number of views, M • number of detector samples, N projection p θ ( r ) • for example, M =1056, N =768 This gives rise to a discrete sinogram p ( n Δ r , m Δθ ) • a matrix with M rows and N columns * Δ r is the detector sampling distance Δθ is the rotation interval between subsequent views sinc • assume also a beam of width Δ s beam aperture Δ s function Δ r Sampling theory will tell us how to Δ s choose these parameters for a given desired object resolution smoothed projection 1 / Δ s Δ θ

Sampling (3) Limiting Aliasing spatial domain frequency domain Aliasing within the sinogram lines (projection aliasing): • to limit aliasing, we must separate the aliases in the frequency domain (at least coinciding the zero-crossings): smoothed projection 1 2 s Δ r ≥ → Δ ≤ r s 2 Δ Δ . • thus, at least 2 samples per beam are required Δ k Δθ Aliasing across the sinogram lines sampling at Δ r k max =1/ Δ r (angular aliasing): k M : number of views, evenly π sinogram in the frequency max Δ θ = distributed around the semi-circle M domain (2 projections with N =12 N : number of detector samples, k 1 / Δ r samples each are shown) max k give rise to N frequency domain Δ = sampled projection N / 2 samples for each projection k k N π for uniform sampling: k max max M Δ θ = Δ → = → = π 1 / Δ s M N / 2 2 Reconstruction: Concept Backprojection: Illustration Given the sinogram p ( r , θ ) we want to recover the object described in ( x , y ) coordinates Recall the early axial tomography method • basically it worked by subsequently “smearing” the acquired p ( r , θ ) across a film plate • for a simple point we would get: This is called backprojection : π ∫ b x y ( , ) B p r { ( , )} p x ( cos y sin , ) d = θ = ⋅ θ + ⋅ θ θ θ 0

Backprojection: Practical Considerations The Fourier Slice Theorem A few issues remain for practical use of this theory: To understand the blurring we need more theory � the Fourier Slice Theorem or Central Slice Theorem • we only have a finite set of M projections and a discrete array of N pixels ( x i , y j ) • it states that the Fourier transform P ( θ , k ) of M a projection p ( r , θ ) is a line across the origin of ∑ b x y ( , ) B p r { ( , )} p x ( cos y sin , ) = θ = ⋅ θ + ⋅ θ θ the Fourier transform F ( k x , k y ) of function f ( x , y ) i j n m i m j m m m 1 = ray pixel polar grid • to reconstruct a pixel ( x i , y j ) there may not be a ray p ( r n , θ n ) (detector sample) in A possible reconstruction procedure would then: the projection set detector • calculate the 1D FT of all projections p ( r m , θ m ), which gives rise to � this requires interpolation (usually samples F ( k x , k y ) sampled on a polar grid (see figure) linear interpolation is used) • resample the polar grid into a cartesian grid (using interpolation) • perform inverse 2D FT to obtain the desired f ( x , y ) on a cartesian grid interpolation However, there are two important observations: • the reconstructions obtained with the simple backprojection appear • interpolation in the frequency domain leads to artifacts blurred (see previous slides) • at the FT periphery the spectrum is only sparsely sampled Filtered Backprojection: Concept Filtered Backprojection: Equation and Result To account for the implications of these two observations, we 1D Fourier ramp-filtering modify the reconstruction procedure as follows: transform of p ( r , θ ) � P ( k , θ ) • filter the projections to compensate for the blurring • perform the interpolation in the spatial domain via backprojection π ∞ ∫ ∫ i 2 kr f x y ( , ) ( P k ( , ) k e π dk d ) = θ ⋅ ⋅ θ � hence the name Filtered Backprojection 0 −∞ Filtering -- what follows is a more practical explanation (for formal proof see the book): inverse 1D Fourier transform � p ( r , θ ) • we need a way to equalize the contributions of all frequencies in the backprojection for all angles FT’s polar grid ramp • this can be done by multiplying each P ( θ , k ) by a ramp function � this way the magnitudes of the existing higher-frequency samples in each Recall the previous (blurred) projection are scaled up to compensate for backprojection illustration their lower amount • now using the filtered projections: • the ramp is the appropriate scaling function since the sample density decreases linearly towards the FT’s periphery not filtered filtered