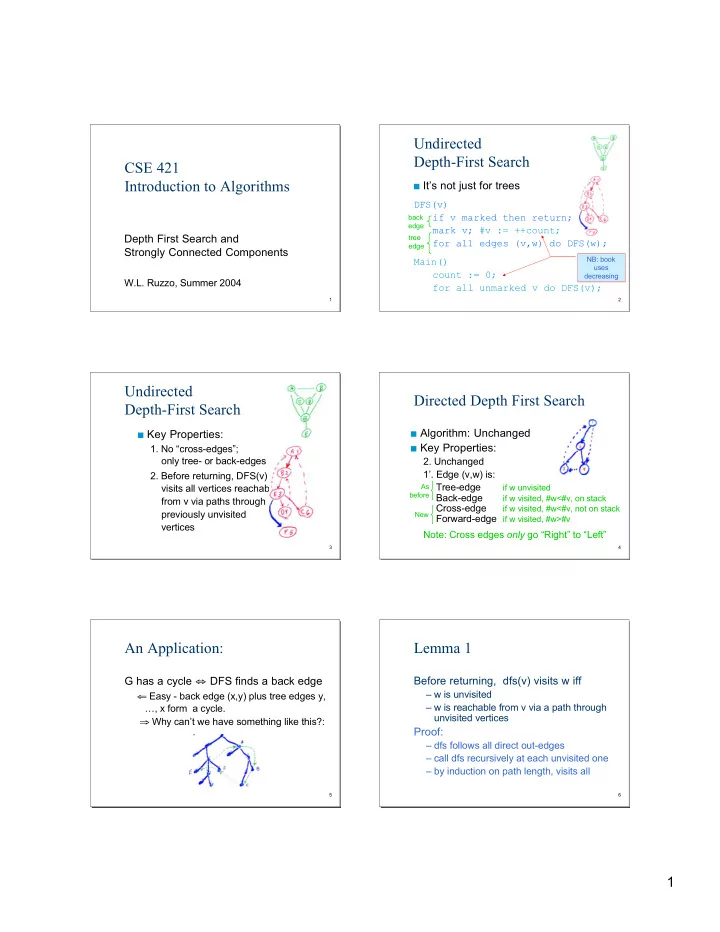
Undirected Depth-First Search CSE 421 Introduction to Algorithms - PDF document

Undirected Depth-First Search CSE 421 Introduction to Algorithms  It’s not just for trees DFS(v) if v marked then return; back edge mark v; #v := ++count; Depth First Search and tree for all edges (v,w) do DFS(w); edge Strongly Connected Components NB: book Main() uses count := 0; decreasing W.L. Ruzzo, Summer 2004 for all unmarked v do DFS(v); 1 2 Undirected Directed Depth First Search Depth-First Search  Algorithm: Unchanged  Key Properties:  Key Properties: 1. No “cross-edges”; only tree- or back-edges 2. Unchanged 1’. Edge (v,w) is: 2. Before returning, DFS(v) Tree-edge visits all vertices reachable As if w unvisited before Back-edge if w visited, #w<#v, on stack from v via paths through Cross-edge if w visited, #w<#v, not on stack previously unvisited New Forward-edge if w visited, #w>#v vertices Note: Cross edges only go “Right” to “Left” 3 4 An Application: Lemma 1 G has a cycle ⇔ DFS finds a back edge Before returning, dfs(v) visits w iff – w is unvisited ⇐ Easy - back edge (x,y) plus tree edges y, – w is reachable from v via a path through …, x form a cycle. unvisited vertices ⇒ Why can’t we have something like this?: Proof: – dfs follows all direct out-edges – call dfs recursively at each unvisited one – by induction on path length, visits all 5 6 1

1 Strongly Connected Components 2 10 3  Defn: G is strongly connected if for all u,v there is a (directed) path from u to v 11 12 and from v to u. 4 8 [Equivalently: 13 there is a circuit through u and v.] 5 9  Defn: a strongly connected component 6 of G is a maximal strongly connected (vertex-induced) subgraph. 7 7 8 1 Uses for SCC’s 2 10 3  Optimizing compilers: – SCC’s in program flow graph = loops 11 12 – SCC’s in call graph = mutual recursion 4 8  Operating Systems: If (u,v) means process u is waiting for process v, SCC’s show 13 deadlocks. 5 9  Econometrics: SCC’s might show highly 6 interdependent sectors of the economy.  Etc. 7 Note: collapsed graph is a DAG 9 10 Directed Acyclic Graphs Two Simple SCC Algorithms  If we collapse each SCC to a • u,v in same SCC iff there are 1 2 10 single vertex we get a directed 3 paths u → v & v → u 11 12 graph with no cycles 4 8 13 5 9 – a directed acyclic graph or DAG 6 7  Many problems on directed • Transitive closure: O(n 3 ) graphs can be solved as follows: 1 – Compute SCC’s and resulting DAG 2 10-12 – Do one computation on each SCC • DFS from every u, v: O(ne) = O(n 3 ) – Do another on the overall DAG 3-9 13 – Example: Spreadsheet evaluation 11 12 2

Goal: Definition  Find all Strongly Connected The root of an SCC is the first vertex in Components in linear time, it visited by DFS. i.e., time O(n+e) Equivalently, the root is the vertex in the (Tarjan, 1972) SCC with the smallest DFS number. 13 14 Exercise: show that each SCC is Lemma 2 Subgoal a contiguous subtree. All members of an SCC are  Can we identify some root? descendants of its root.  How about the root of the first SCC completely explored (returned from) Proof: by DFS? – all members are reachable from all others – so, all are reachable from its root  Key idea: no exit from first SCC – all are unvisited when root is visited (first SCC is leftmost “leaf” in collapsed DAG) – so, all are descendants of its root (Lemma 1) 15 16 v 1 x Definition 2 10 x is an exit from v (from v’s subtree) if 3 – x is not a descendant of v, but 11 12 – x is the head of a (cross- or back-) edge 4 8 from a descendant of v (including v itself) 13 5 9 NOTE: #x < #v # root exits 6 1 1 - 2 2 - 3 3 - 4, 5 3 3 Ex: node #1 cannot have an exit. 6 3 3, 5 7 7 3 5 8, 9 3 7 10 10 2, 8 17 11, 12 10 10 18 13 13 - 3

r z ? Lemma 3: Lemma 4: v r x x Nonroots have exits No Escaping 1st Root Idea: Follow cycle to root If v is not a root, then v has an exit. If r is the first root from which dfs returns, then r Idea: Exit ⇒ Bigger Cycle has no exit Proof: Proof (by contradiction) : – let r be root of v’s SCC – Suppose x is an exit – r is a proper ancestor of v (Lemma 2) – let z be root of x’s SCC – let x be the first vertex that is not a – r not reachable from z, else in same SCC descendant of v on a path v → r . – #z ≤ #x (z ancestor of x; Lemma 2) – x is an exit – #x < #r (x is an exit from r) – #z < #r, no z → r path, so return from z first Cor (contrapositive) : If v has no exit, then v is a root. – Contradiction NB: converse not true; some roots do have exits 19 20 1 How to Find Exits (in 1 st component) 2 10  All exits x from v have #x < #v 3 11  Suffices to find any of them, e.g. min # 12  Defn: 4 8 LOW(v) = min({ #x | x an exit from v} ∪ {#v}) 13  Calculate inductively: 5 9 LOW(v) = min of: x 1 # root exits LOW 6 1 1 - v x 2 – #v 2 2 - 3 3 - 3 1 st root: – { LOW(w) | w a child of v } w 1 w 2 w 3 4, 5 3 3 3 LOW(v)=v 6 3 3, 5 3 – { #x | (v,x) is a back- or cross-edge } 7 7 3 5 5 8, 9 3 7 7  1 st root : LOW(v)=v 10 10 2, 8 21 22 11, 12 10 10 13 13 - r v Finding Other Components Lemma 3’ x  Key idea: No exit from If v is not a root, then v has an exit . – 1 st SCC Proof: in v’s SCC – 2 nd SCC, except maybe to 1 st – let r be root of v’s SCC – 3 rd SCC, except maybe to 1 st and/or 2 nd – r is a proper ancestor of v (Lemma 2) – ... – let x be the first vertex that is not a descendant of v on a path v → r . – x is an exit in v’s SCC Cor: If v has no exit , then v is a root. in v’s SCC 23 24 4

z ? k th r Lemma 4’ How to Find Exits (in 1 st component) x k th If r is the first root from which dfs  All exits x from v have #x < #v returns, then r has no exit  Suffices to find any of them, e.g. min # Proof: except possibly  Defn: – Suppose x is an exit to the first (k-1) LOW(v) = min({ #x | x an exit from v } ∪ {#v}) – let z be root of x’s SCC components  Calculate inductively: – r not reachable from z, else in same SCC LOW(v) = min of: – #z ≤ #x (z ancestor of x; Lemma 2) and x not in first – #x < #r (x is an exit from r) – #v (k-1) components – #z < #r, no z → r path, so return from z first – { LOW(w) | w a child of v } – Contradiction – { #x | (v,x) is a back- or cross-edge } i.e., x in first (k-1) 25 26 1 SCC Algorithm #v = DFS number v.low = LOW(v) 2 v.scc = component # 10 SCC(v) 3 #v = vertex_number++; v.low = #v; push(v) 11 for all edges (v,w) 12 if #w == 0 then 4 8 SCC(w); v.low = min(v.low, w.low) // tree edge else if #w < #v && w.scc == 0 then 13 v.low = min(v.low, #w) // cross- or back-edge 5 9 if #v == v.low then // v is root of new scc # root exits LOW 6 1 1 - 1 scc#++; 2 2 - 2 3 3 - 3 repeat 4, 5 3 3 3 6 3 3, 5 3 w = pop(); w.scc = scc#; // mark SCC members 7 7 3 5 5 until w==v 8, 9 3 7 7 10 10 2, 8 10 27 28 11, 12 10 10 10 13 13 - 13 Complexity Where to start  Unlike undirected DFS, start vertex matters  Look at every edge once  Add “outer loop”:  Look at every vertex (except via in- edge) at most once mark all vertices unvisited while there is unvisited vertex v do scc(v)  Time = O(n+e)  Exercise: redo example starting from another vertex, e.g. #11 or #13 (which become #1) 29 30 5

v Low(v) v Low(v) Example Example dfs# v root exits low(v) 1 2 A 3 4 5 B C D 6 E F 31 32 6