t dt = 2 t t dt t t dt 1 erf x e 0 0 - PowerPoint PPT Presentation

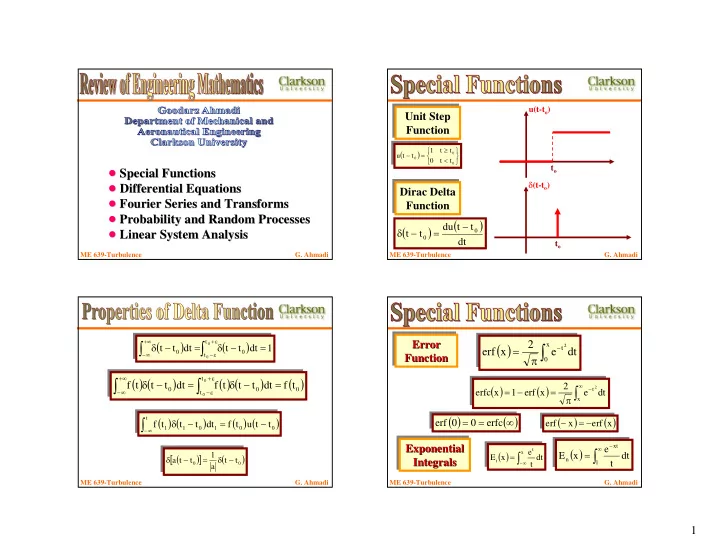
u(t-t o ) Unit Step Unit Step Function Function ⎧ ≥ ⎫ 1 t t ( ) − = 0 ⎨ ⎬ u t t < 0 ⎩ 0 t t ⎭ 0 t o ! Special Functions ! Special Functions δ (t-t o ) ! Differential Equations ! Differential Equations Dirac Delta Dirac Delta ! Fourier Series and Transforms ! Fourier Series and Transforms Function Function ! Probability and Random Processes ! Probability and Random Processes ( ) − ( ) du t t δ − = ! Linear System Analysis ! 0 Linear System Analysis t t 0 dt t o ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi +∞ ( ) + ε ( ) Error ∫ ∫ t ( ) Error Error 2 δ − = δ − = x 0 ∫ t dt = − 2 t t dt t t dt 1 erf x e 0 0 − ∞ − ε Function t π Function Function 0 0 +∞ ( ) ( ) + ε ( ) ( ) ( ) ∫ ∫ t δ − = δ − = 0 f t t t dt f t t t dt f t ( ) ( ) 2 ∞ ∫ t dt − = − = 2 0 0 0 − ∞ − ε erfc x 1 erf x e t 0 π x ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = ∞ ∫ ∞ t − = − δ − = − erf 0 0 erfc erf x erf x f t t t dt f t u t t 1 1 0 1 0 0 − Exponential − ( ) ∫ Exponential xt Exponential ∞ e ( ) ∫ ∞ t e = x [ ( ) ] 1 ( ) = E x dt δ − = δ − E x dt Integrals a t t t t n Integrals Integrals i − t t 1 0 0 a ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi 1

Fourier Integral Representation Fourier Integral Representation Fourier Integral Representation ( ) ⎧ ⎫ + ∞ ( ) df df x ∫ − ω ℑ = = ω ω ) ( ) i x ⎨ ⎬ e dx i f ( ) 1 + ∞ + ∞ ( ∫ ∫ = ω − ′ ′ ′ ω i x x f x e f x d x d ⎩ ⎭ − ∞ dx dx π − ∞ − ∞ 2 Fourier Transform (Exponential) Fourier Transform (Exponential) Fourier Transform (Exponential) ⎧ ⎫ ⎧ ⎫ ( ) +∞ ( ) 2 n ( ) ( ) ∫ d f ( ) d f − ω ′ ′ ′ ω = i x ℑ = − ω ω ℑ = ω ω n f e f x d x 2 ⎨ ⎬ ⎨ ⎬ i f f − ∞ n 2 ⎩ ⎭ ⎩ ⎭ dx dx + ∞ ( ) 1 ( ) ∫ = ω ω ω i x f x e f d π − ∞ 2 ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi ( ) ( ) ω f f x 2 ( ) d f df + + = δ − − ∞ < < +∞ a bf x x ( ) ( ) ω f + ω x i x f x x e 0 0 2 dx dx 1 0 ( ) − ω δ x − i x e x 0 0 α Taking Fourier Transform 2 Taking Fourier Transform − α Taking Fourier Transform x e ω + α 2 2 ( ) ( ) ( ) ( ) +∞ ( ) ( ) ( ) ( ) ( ) ∫ ω ω = ξ − ξ ξ f f − ω f x * f x f f x d − ω ω + ω ω + ω = 2 i x 1 2 1 2 − ∞ 1 2 f ai f b f e 0 [ ] ( ) ( ) ω π δ ω − ω + δ ω + ω cos x 0 0 0 ( ) α ω + α + β ( ) − α 2 2 2 − ω β 2 ω − x i x i x x e cos x ( ) e ( ) 0 ( ) 1 + ∞ e 0 ∫ ω = ω − β − α 2 + α ω = ω 2 2 2 2 2 4 f f x d ( ) − ω + ω π − ω + ω ⎡ α ⎤ α α + β 2 2 2 2 4 b ia − ∞ 2 b ia − α β + β x e ⎢ cos x sin x ⎥ ( ) β 2 ω − β − α + α ω ⎣ ⎦ 2 2 2 2 2 4 ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi 2

( ) ( ) F Y (y) ω f x f ( ) ( ) ⎡ ⎤ ⎧ ⎫ ⎧ ⎫ − α 2 x 2 β π ω + β 2 ω − β 2 e cos x − + − ⎢ ⎨ ⎬ ⎨ ⎬ ⎥ exp exp α α α 1 ⎢ 2 2 ⎥ 2 ⎩ 4 ⎭ ⎩ 4 ⎭ ⎣ ⎦ e α − π ⎧ ω ⎫ 2 x 2 2 − ⎨ ⎬ exp α α 2 ⎩ 4 ⎭ ( ) n d ( ) i ω n δ x y n dx ( ) ⎧ ⎫ 2 J 0 x ⎪ ω < ⎪ 1 ( ) ( ) { } ⎨ ⎬ − ω 2 1 = ≤ ≤ ≤ ⎪ ⎪ F y P Y y 0 F y 1 ⎩ ⎭ 0 elsewhere Y Y ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi f Y (y) ( ) { } +∞ ( ) Expected ( ) dF y Expected ∫ Expected = = = ( ) +∞ ( ) Y f y ∫ ∞ = = E Y Y yf y dy F 1 f y dy Y dy Value Y Y Y − ∞ Value − ∞ Value { ( ) } ( ) +∞ ( ) ( ) ∫ = = E g Y g Y g y f y dy Y − ∞ y Variance Variance Variance { } ( ) { } { } ( ) ( ) ( ) ∫ y 2 2 < ≤ = = − σ = − = − 2 2 2 P y Y y f y dy F y F y E Y Y E Y Y 1 2 Y Y 2 Y 1 y Y 1 ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi 3

X(t) Time = ∫ ( ) 1 ( ) { ( ) } Time Time T ≈ X t X t dt E X t Averaging Averaging Averaging T 0 Autocorrelation Autocorrelation Autocorrelation t ( ) { ( ) ( ) } ( ) ( ) 1 ∫ T τ = + τ = + τ R E X t X t X t X t dt xx T 0 { ( ) } +∞ ( ) { } ∫ = ( ) ( ) ( ) E X t xf x , t dx = = 2 2 R 0 E X t X t X − ∞ xx ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi H( ω )=System Function h(t)=Impulse Response H( ω ω )=System Function ( ) +∞ ( ) h(t)=Impulse Response h(t)=Impulse Response H( )=System Function ∫ ω = − ωτ τ τ i S e R d ( ) xx xx − ∞ h t X(t) f(t) ( ) ω H ( ) 1 + ∞ ( ) ∫ τ = ωτ ω ω i R e S d π xx xx − ∞ ( ) ( ) ( ) 2 ( ) +∞ ( ) ∫ t ∫ = − τ τ τ − ω ω = i t X t h t f d H e h t dt − ∞ 0 ( ) ( ) 1 ~ 2 +∞ ~ ( ) ( ) ω = ω ∫ = ∫ − ω ω = ( ) +∞ ( ) ( ) ( ) ( ) S X i t X e X t dt − τ τ τ = X t h t f d h t * f t xx − ∞ T − ∞ ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi 4

Fourier ( ) ( ) ( ) ~ ( ) Fourier Fourier ( ) ~ ω = ω ω + α = − α = & x H f t x x f t h t e Transform Transform Transform ( ) + ζω + ω = ( ) 1 ( ) 1 ( ) ( ) ( ) ( ) 2 2 2 & & & ω = ω = ω 2 ω = ω 2 ω x 2 x x f t S x H f H S 0 0 xx ff T T ( ) ( ) ( ) Spectral Spectral ω = ω 2 ω Spectral ( ) 1 − ζω S H S = ω t h t e sin t ω = ω − ζ 0 Relationship 2 1 Relationship Relationship xx ff ω d d 0 d ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi ( ) − 3 x x + α = & + + α = Finite x x n t i 1 i 2.5 x n + ∆ i 1 i 2 difference t 1.5 White Noise 1 ∆ 0.5 1 t = + 0 x x n -0.5 + + α ∆ + α ∆ i 1 i i 1 t 1 t i = -1 x x ( t ) -1.5 i -2 = + ∆ α ∆ << -2.5 x x t n for t 1 + i 1 i i -3 0 0.0001 0.0002 0.0003 0.0004 0.0005 Time (s) 1 1 = + α ∆ >> x x n for t 1 + i 1 α ∆ i α i t ME 639-Turbulence G. Ahmadi ME 639-Turbulence G. Ahmadi 5