MAT 132 8.1 Sequences n th term Examples In a sequence order - PowerPoint PPT Presentation

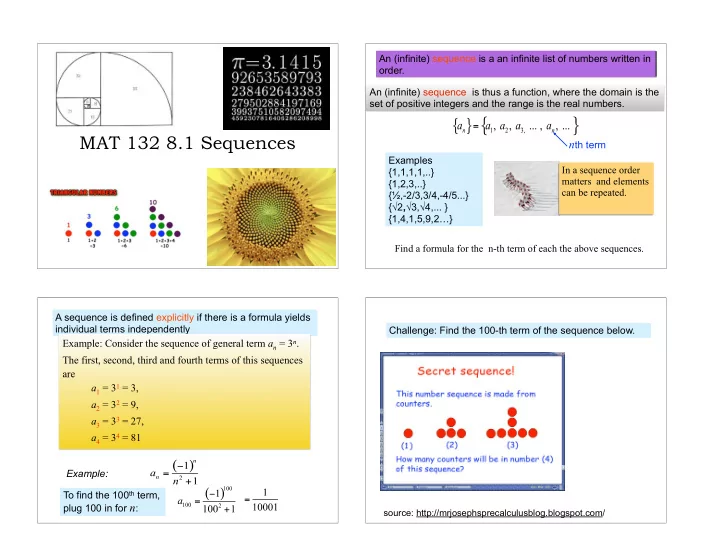
An (infinite) sequence is a an infinite list of numbers written in order. An (infinite) sequence is thus a function, where the domain is the set of positive integers and the range is the real numbers. MAT 132 8.1 Sequences n th term Examples In a sequence order {1,1,1,1,..} matters and elements {1,2,3,..} can be repeated. { ½ ,-2/3,3/4,-4/5...} { √ 2 , √ 3, √ 4,... } {1,4,1,5,9,2 … } Find a formula for the n-th term of each the above sequences. 1 A sequence is defined explicitly if there is a formula yields individual terms independently Challenge: Find the 100-th term of the sequence below. Example: Consider the sequence of general term a n = 3 n . The first, second, third and fourth terms of this sequences are a 1 = 3 1 = 3, a 2 = 3 2 = 9, a 3 = 3 3 = 27, a 4 = 3 4 = 81 Example: To find the 100 th term, plug 100 in for n : source: http://mrjosephsprecalculusblog.blogspot.com/

A sequence is defined recursively if there is a formula that relates a n to previous terms. Example 1: Example 2: Fibonacci sequence b 1 =1,b 2 =1,b n =b n-1 +b n-2 for n ≥ 3 Example 3: Collatz sequences Fibonacci sequence in nature Example 1: Can you give an explicit definition of the sequence in Example 1? \ 6 The golden angle, is 137.5 degrees. Example of sequences defined recursively: Collatz sequences Conjecture: f(n) = n/2 if n is even No matter which 3n+1 otherwise number you start 1, 1, 2, 3, 5, 8, 13, 21 , 34 , 55 , 89... Start with a positive integer, say, 10, See more from Vi Hart “Open letter to Nickelodeaon” � from, the sequence https://www.youtube.com/watch?v=ahXIMUkSXX0 � � a 1 =10 always reaches 1 https://www.youtube.com/watch?v=gBxeju8dMho a 2 =f(a 1 )=5 2011: The Collatz a 3 =f (a 2 )=16 algorithm has and so on. been tested and found to always This gives a recursively defined sequence for each “starting reach 1 for all number”, which seems to end in 1, 1,1,1.. for all starting numbers up to numbers. 5 . 7 x 10 18 (Starting at a different number, you’ll obtained a different sequence ) 7 8

Example of sequences An arithmetic sequence is a sequence such that the defined recursively: difference between consecutive terms is constant. Collatz sequences Examples: f(n) = n/2 if n is even 3n+1 otherwise Start with a positive integer, say, 10, a 1 =10 Arithmetic sequences can a 2 =f(a 1 )=5 be defined recursively: a 3 =f (a 2 )=16 and so on. or explicitly: 9 A sequence is defined explicitly if there is a formula that A sequence is geometric if the quotient of consecutive allows you to find individual terms independently. terms is constant. That is consecutive terms have the � same ratio. Ex: a n =n/(n 2 +1) Example: Any real-valued function defined on the positive real yields a sequence (explicitly defined). � Example: f(x)=(x+2) ½ n-th of the sequence: a n =(n+2) ½ Geometric sequences can a n = a n-1 . r A sequence is defined recursively if there is a formula that be defined recursively: relates a n to previous terms. An arithmetic sequence has a common difference a n = a 1 . r n-1 or explicitly: between terms. An geometric sequence has a common ratio between terms.

Write the first terms of Consider the sequence the sequence Plot these terms Plot the sequence as on a number line a function The terms in this sequence do not get close to any (single) number when n grows. The terms in this sequence get closer and closer to 1. The sequence CONVERGES to 1. Recall: The sequence {a n } converges to L if we can make a n as A sequence is geometric if the quotient of consecutive close to L as we want for all sufficiently large n. In terms is constant. That is consecutive terms have the other words, the value of the a n ’s approach L as n same ratio. approaches infinity. Example: We write 
 Example Geometric sequences can a n = a n-1 . r be defined recursively: Otherwise, that is if {a n } does not converges to any number, we say that {a n } diverges . Example a n = a 1 . r n-1 or explicitly: Can you find examples of convergent geometric 15 sequence? And of diverent geometric sequences?

Determine whether the sequences below are convergent. 1. a n = 3 n , 2. a n =( ½ ) n Examples: Study whether the sequences below 3. a n =(-1) n converge using the theorem above (if possible) 4. a n =(-2) n 5. a n =(-0.1) n 6. an =(3/2) n Example: The above theorem cannot be used to prove that the sequence a n =1/n! converges. Why? 17 18 Example: Below is the n-th term of some sequences Determine whether the corresponding sequences converge and if so, find the limit. 1. a n =1/n 2. a n =1/n + 3(n+1)/n 2 3. b n = (a n ) 2 (a n as in 2.). 4. a n =n!/(n+1)! 5. a n =(n+1)!/n! 6. a n = 1/ln(n). 7. a n = n/ln(n). 8. a n = n . sin(1/n). 19 20

The squeeze theorem Give examples of 1.Increasing, convergent sequences. 2.Decreasing convergent sequences. Example: Use the “squeeze 3.Increasing divergent sequences. theorem” above to determine 4.Decreasing divergent sequences. whether the sequence {a n } defined 5.Convergent sequences that are not increasing and not decreasing by a n = (n 2 +1)/n 3 is converges and if 6.Divergent sequences that are not increasing and not so, find the limit. decreasing � 21 22 List of Types of sequences and examples Example: Compute the arc length Example: Compute the arc length of the circle r = sin ϴ � the graph of the curve y=x 3/2 , � Defined explicitly Ex: a n =n/(n 2 +1) ϴ in [0,2 π ] x in [0,5] Defined recursively Ex: a 1 =1, a 2 =1, a n =a n-1 +a n-2 , n ≥ 3. Defined by function POLAR Example: f(x)=(x+2) ½ a n =(n+2) ½ FUNCTION Convergent a n =1/n Divergent, a n =n or a n =(-1) n Example: Compute the length arc Example: Compute the length two “Tricks” to determine arcs of the cycloid x= ϴ - sin ϴ , y=1- of the spiral r = e ϴ � whether sequences Arithmetic a n =a 1 + (n-1) . d cos ϴ . (Hint (1-cos(t))=2 sin 2 (t/2)) in [0,2 π ] are convergent or Geometric a n =a 1 . r n-1 PARAMETRIC POLAR divergent and to find the limit if they are convergent. Increasing a n =(1-1/n) • Squeeze theorem Decreasing a n =1/n • L’Hopital Bounded a n =sin(n)