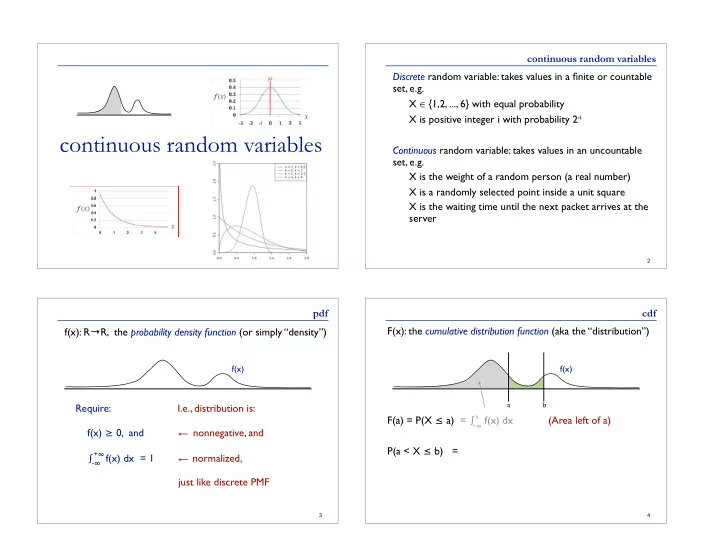
continuous random variables Continuous random variable: takes values - PowerPoint PPT Presentation

continuous random variables Discrete random variable: takes values in a finite or countable set, e.g. X ∈ {1,2, ..., 6} with equal probability X is positive integer i with probability 2 -i continuous random variables Continuous random variable: takes values in an uncountable set, e.g. X is the weight of a random person (a real number) X is a randomly selected point inside a unit square X is the waiting time until the next packet arrives at the server 2 pdf cdf f(x): R → R, the probability density function (or simply “density”) F(x): the cumulative distribution function (aka the “distribution”) f(x) f(x) a b Require: I.e., distribution is: F(a) = P(X ≤ a) = ∫ f(x) dx (Area left of a) a − ∞ f(x) ≥ 0, and nonnegative, and P(a < X ≤ b) = + ∞ ∫ f(x) dx = 1 normalized, - ∞ just like discrete PMF 3 4

cdf cdf F(x): the cumulative distribution function (aka the “distribution”) F(x): the cumulative distribution function (aka the “distribution”) f(x) f(x) a b a b F(a) = P(X ≤ a) = ∫ f(x) dx (Area left of a) a F(a) = P(X ≤ a) = ∫ f(x) dx (Area left of a) a − ∞ − ∞ P(a < X ≤ b) = F(b) - F(a) (Area between a and b) P(a < X ≤ b) = F(b) - F(a) (Area between a and b) Relationship between f(x) and F(x)? 5 6 cdf why is it called a density? F(x): the cumulative distribution function (aka the “distribution”) Densities are not probabilities; e.g. may be > 1 P(X = a) = lim ε→ 0 P(a- ε < X ≤ a) = F(a)-F(a) = 0 f(x) I.e., the probability that a continuous r.v. falls at a specified point is zero. But a b F(a) = P(X ≤ a) = ∫ f(x) dx (Area left of a) a the probability that it falls near that point is proportional to the density : − ∞ f(x) P(a < X ≤ b) = F(b) - F(a) (Area between a and b) A key relationship: a- ε /2 a a+ ε /2 a f(x) = F(x), since F(a) = ∫ f(x) dx, d dx − ∞ 7 8

why is it called a density? sums and integrals; expectation Densities are not probabilities; e.g. may be > 1 Much of what we did with discrete r.v.s carries over almost unchanged, with Σ x ... replaced by ∫ ... dx P(X = a) = lim ε→ 0 P(a- ε < X ≤ a) = F(a)-F(a) = 0 I.e., E.g. the probability that a continuous r.v. falls at a specified point is zero. For discrete r.v. X, E [ X ] = Σ x xp ( x ) But For continuous r.v. X, the probability that it falls near that point is proportional to the density : f(x) P(a - ε /2 < X ≤ a + ε /2) = F(a + ε /2) - F(a - ε /2) ≈ ε • f(a) a- ε /2 a a+ ε /2 I.e., in a large random sample, expect more samples where density is higher (hence the name “density”). 9 10 sums and integrals; expectation example 1 Let Much of what we did with discrete r.v.s carries over almost f ( x ) unchanged, with Σ x ... replaced by ∫ ... dx -1 0 1 2 What is F(x)? What is E(X)? 1 E.g. F ( x ) For discrete r.v. X, E [ X ] = Σ x xp ( x ) -1 0 1 2 For continuous r.v. X, Why? (a) We define it that way (b) The probability that X falls “near” x, say within x±dx/2, is ≈ f(x)dx, so the “average” X should be ≈ Σ xf(x)dx (summed over grid points spaced dx apart on the real line) and the limit of that as dx → 0 is ∫ xf(x)dx 11 12

example properties of expectation 1 Linearity Let f ( x ) -1 0 1 2 E[aX+b] = aE[X]+b 1 still true, just as for discrete F ( x ) E[X+Y] = E[X]+E[Y] -1 0 1 2 Functions of a random variable E[g(X)] = ∫ g(x)f(x)dx just as for discrete, but w/integral Alternatively, let Y = g(X), find the density of Y, say f Y , and directly compute E[Y] = ∫ yf Y (y)dy. 13 14 variance example 1 Definition is same as in the discrete case Let f ( x ) Var[X] = E[(X- μ ) 2 ] where μ = E[X] -1 0 1 2 1 Identity still holds: F ( x ) Var[X] = E[X 2 ] - (E[X]) 2 proof “same” -1 0 1 2 15 16

example continuous random variables: summary 1 Let f ( x ) Continuous random variable X has density f(x), and -1 0 1 2 1 F ( x ) -1 0 1 2 17 uniform random variables uniform random variables X ~ Uni( α , β ) is uniform in [ α , β ] The Uniform Density Function Uni(0.5,1.0) X ~ Uni( α , β ) is uniform in [ α , β ] 2.0 1.5 The Uniform Density Function Uni(0.5,1.0) f(x) 1.0 2.0 2.0 0.5 0.0 0.0 0.5 1.0 1.5 x 1.5 f(x) 1.0 Yes, you should review your basic if α≤ a ≤ b ≤β : calculus; e.g., these 0.5 2 integrals would be good practice. 0.0 0.0 0.5 1.0 1.5 0.5 ( α ) 1.0 ( β ) x


 waiting for “events” exponential random variables Radioactive decay: How long until the next alpha particle? X ~ Exp( λ ) Customers: how long until the next customer/packet arrives at the The Exponential Density Function checkout stand/server? Buses: How long until the next #71 bus arrives on the Ave? 2.0 Yes, they have a schedule, but given the vagaries of traffic, riders with-bikes-and-baby- λ = 2 carriages, etc., can they stick to it? 1.5 Assuming events are independent, happening at some fixed average f(x) 1.0 rate of λ per unit time – the waiting time until the next event is exponentially distributed (next slide) 0.5 λ = 1 0.0 -1 0 1 2 3 4 21 x exponential random variables Relation to Poisson X ~ Exp( λ ) Same process, different measures: Poisson: how many events in a fixed time ; 
 Exponential: how long until the next event λ is avg # per unit time; 
 1/ λ is mean wait = 1- F ( t ) Memorylessness: Assuming exp distr , if you’ve waited s minutes, prob of waiting t more is exactly same as s = 0 24

Suppose that the number of miles that a car can run before its Time it takes to check someone out at a grocery store is exponential battery wears out is exponentially distributed with an average with with an average value of 10. value of 10,000 miles. If the car has already been used for 2000 If someone arrives to the line immediately before you, what is the miles, and the owner wants to take a 5000 mile trip, what is the probability that you will have to wait between 10 and 20 minutes? probability she will be able to complete the trip without replacing the battery? T ∼ exp (10 − 1 ) N ∼ exp (1 / 10 , 000) Z 20 Pr ( N ≥ 7000 | N ≥ 2000) = Pr ( N ≥ 7000) 1 10 e − x 10 dx Pr (10 ≤ T ≤ 20) = Pr ( N ≥ 2000) 10 dy = 1 y = x Pr ( N ≥ 7000) = e − 7000 / 10000 10 dx 10 Pr ( N ≥ 2000) = e − 2000 / 10000 Z 2 2 = − e − y � = ( e − 1 − e − 2 ) Pr (10 ≤ T ≤ 20) = e − y dy = � answer = e − 5000 / 10000 = e − 0 . 5 � 1 1 25 26 normal random variables changing μ , σ X is a normal (aka Gaussian) random variable X ~ N( μ , σ 2 ) 0.5 0.5 µ = 0 0.4 0.4 0.3 0.3 σ = 1 µ = 0 0.2 0.2 σ = 2 0.1 0.1 0.0 0.0 -10 -5 0 5 10 -10 -5 0 5 10 The Standard Normal Density Function 0.5 μ ± σ 0.5 μ ± σ µ = 4 0.5 0.4 0.4 µ = 0 0.4 0.3 0.3 σ = 1 µ = 4 0.3 σ = 1 f(x) 0.2 0.2 0.2 σ = 2 0.1 0.1 0.1 0.0 0.0 0.0 -10 -5 0 5 10 -10 -5 0 5 10 -3 -2 -1 0 1 2 3 μ ± σ μ ± σ density at μ is ≈ .399/ σ x μ ± σ 28