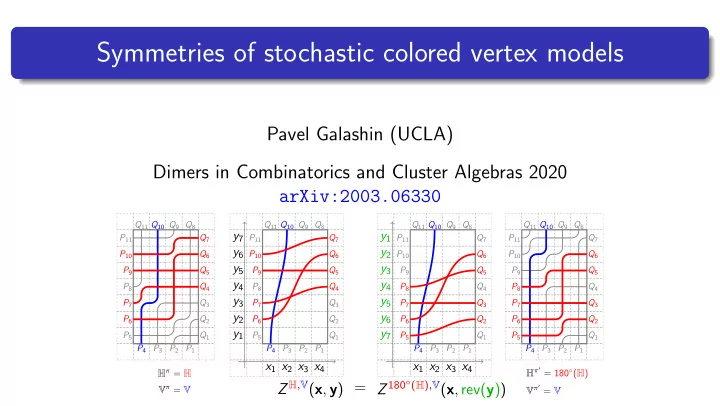
Symmetries of stochastic colored vertex models Pavel Galashin (UCLA) - PowerPoint PPT Presentation

Symmetries of stochastic colored vertex models Pavel Galashin (UCLA) Dimers in Combinatorics and Cluster Algebras 2020 arXiv:2003.06330 Q 11 Q 10 Q 9 Q 8 Q 11 Q 10 Q 9 Q 8 Q 11 Q 10 Q 9 Q 8 Q 11 Q 10 Q 9 Q 8 y 7 y 1 P 11 Q 7 P 11 Q 7 P 11 Q 7 P 11 Q 7 y 6 y 2 P 10 Q 6 P 10 Q 6 P 10 Q 6 P 10 Q 6 y 5 y 3 P 9 Q 5 P 9 Q 5 P 9 Q 5 P 9 Q 5 y 4 y 4 P 8 Q 4 P 8 Q 4 P 8 Q 4 P 8 Q 4 y 3 y 5 P 7 Q 3 P 7 Q 3 P 7 Q 3 P 7 Q 3 y 2 y 6 P 6 Q 2 P 6 Q 2 P 6 Q 2 P 6 Q 2 y 1 y 7 P 5 Q 1 P 5 Q 1 P 5 Q 1 P 5 Q 1 P 4 P 3 P 2 P 1 P 4 P 3 P 2 P 1 P 4 P 3 P 2 P 1 P 4 P 3 P 2 P 1 x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 H π ′ = 180 ◦ ( H ) H π = H Z H , V ( x , y ) = Z 180 ◦ ( H ) , V ( x , rev( y )) V π ′ = V V π = V

Stochastic colored six-vertex model • Introduced in 2016: [KMMO16] A. Kuniba, V. V. Mangazeev, S. Maruyama, and M. Okado. Stochastic R matrix for U q ( A (1) n ). Nuclear Phys. B , 913:248–277, 2016.

Stochastic colored six-vertex model • Introduced in 2016: [KMMO16] A. Kuniba, V. V. Mangazeev, S. Maruyama, and M. Okado. Stochastic R matrix for U q ( A (1) n ). Nuclear Phys. B , 913:248–277, 2016. • Limiting cases include many other interesting probabilistic models

Stochastic colored six-vertex model • Introduced in 2016: [KMMO16] A. Kuniba, V. V. Mangazeev, S. Maruyama, and M. Okado. Stochastic R matrix for U q ( A (1) n ). Nuclear Phys. B , 913:248–277, 2016. • Limiting cases include many other interesting probabilistic models

Stochastic colored six-vertex model • Introduced in 2016: [KMMO16] A. Kuniba, V. V. Mangazeev, S. Maruyama, and M. Okado. Stochastic R matrix for U q ( A (1) n ). Nuclear Phys. B , 913:248–277, 2016. • Limiting cases include many other interesting probabilistic models

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 n = 11 10 9 8 7 6 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 0 < q < 1 is fixed 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 When two paths of colors c 1 < c 2 enter a n = 11 square from the bottom/left, they form either a crossing or an elbow 10 → c 2 c 2 or c 2 p 9 c 1 c 1 c 1 Probability: 1 − p 8 p 7 c 1 → c 1 or c 1 p 6 c 2 c 2 c 2 Probability: q p 1 − q p 5 0 < q < 1 is fixed spectral parameter p depends on the square 4 3 2 1

n lattice paths of colors 1 , 2 , . . . , n move up/right on Z 2 Q 11 Q 10 Q 9 Q 8 When two paths of colors c 1 < c 2 enter a y 7 P 11 Q 7 square from the bottom/left, they form y 6 either a crossing or an elbow P 10 Q 6 → c 2 c 2 or c 2 p y 5 P 9 Q 5 c 1 c 1 c 1 y 4 Probability: 1 − p P 8 Q 4 p y 3 P 7 Q 3 c 1 → c 1 or c 1 p y 2 P 6 Q 2 c 2 c 2 c 2 Probability: q p 1 − q p y 1 P 5 Q 1 0 < q < 1 is fixed P 4 P 3 P 2 P 1 spectral parameter p depends on the square p i , j = y j − x i x 1 x 2 x 3 x 4 y j − qx i

→ or Q 11 Q 10 Q 9 Q 8 c 2 c 2 c 2 p y 7 P 11 Q 7 c 1 c 1 c 1 y 6 P 10 Q 6 Probability: 1 − p p y 5 P 9 Q 5 y 4 P 8 Q 4 c 1 → c 1 or c 1 p y 3 P 7 Q 3 y 2 c 2 c 2 c 2 P 6 Q 2 Probability: q p 1 − q p y 1 P 5 Q 1 y j − x i p i , j = P 4 P 3 P 2 P 1 y j − qx i x 1 x 2 x 3 x 4

→ or Q 11 Q 10 Q 9 Q 8 c 2 c 2 c 2 p y 7 P 11 Q 7 c 1 c 1 c 1 y 6 P 10 Q 6 Probability: 1 − p p y 5 P 9 Q 5 y 4 P 8 Q 4 c 1 → c 1 or c 1 p y 3 P 7 Q 3 y 2 c 2 c 2 c 2 P 6 Q 2 Probability: q p 1 − q p y 1 P 5 Q 1 y j − x i p i , j = P 4 P 3 P 2 P 1 y j − qx i 2 MN pipe dreams − x 1 x 2 x 3 x 4 → n ! permutations  1 2 3 4 5 6 7 8 9 10 11  π = ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓   2 1 3 10 8 6 4 11 5 7 9

→ or Q 11 Q 10 Q 9 Q 8 c 2 c 2 c 2 p y 7 P 11 Q 7 c 1 c 1 c 1 y 6 P 10 Q 6 Probability: 1 − p p y 5 P 9 Q 5 y 4 P 8 Q 4 c 1 → c 1 or c 1 p y 3 P 7 Q 3 y 2 c 2 c 2 c 2 P 6 Q 2 Probability: q p 1 − q p y 1 P 5 Q 1 y j − x i p i , j = P 4 P 3 P 2 P 1 y j − qx i 2 MN pipe dreams − x 1 x 2 x 3 x 4 → n ! permutations For each π ∈ S n , let H π and V π record  1 2 3 4 5 6 7 8 9 10 11  the endpoints of all “horizontal” and π = ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ “vertical” pipes   2 1 3 10 8 6 4 11 5 7 9

→ or Q 11 Q 10 Q 9 Q 8 c 2 c 2 c 2 p y 7 P 11 Q 7 Q 7 c 1 c 1 c 1 y 6 P 10 P 10 Q 6 Q 6 Probability: 1 − p p y 5 P 9 P 9 Q 5 Q 5 y 4 P 8 Q 4 Q 4 c 1 → c 1 or c 1 p y 3 P 7 P 7 Q 3 y 2 c 2 c 2 c 2 P 6 P 6 Q 2 Probability: q p 1 − q p y 1 P 5 Q 1 y j − x i p i , j = P 4 P 3 P 2 P 1 y j − qx i 2 MN pipe dreams − x 1 x 2 x 3 x 4 → n ! permutations For each π ∈ S n , let H π and V π record  1 2 3 4 5 6 7 8 9 10 11  the endpoints of all “horizontal” and π = ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ “vertical” pipes   2 1 3 10 8 6 4 11 5 7 9 H π = { (6 , 6) , (7 , 4) , (9 , 5) , (10 , 7) }

→ or Q 11 Q 10 Q 10 Q 9 Q 8 c 2 c 2 c 2 p y 7 P 11 Q 7 c 1 c 1 c 1 y 6 P 10 Q 6 Probability: 1 − p p y 5 P 9 Q 5 y 4 P 8 Q 4 c 1 → c 1 or c 1 p y 3 P 7 Q 3 y 2 c 2 c 2 c 2 P 6 Q 2 Probability: q p 1 − q p y 1 P 5 Q 1 y j − x i p i , j = P 4 P 4 P 3 P 2 P 1 y j − qx i 2 MN pipe dreams − x 1 x 2 x 3 x 4 → n ! permutations For each π ∈ S n , let H π and V π record  1 2 3 4 5 6 7 8 9 10 11  the endpoints of all “horizontal” and π = ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ “vertical” pipes   2 1 3 10 8 6 4 11 5 7 9 H π = { (6 , 6) , (7 , 4) , (9 , 5) , (10 , 7) } V π = { (4 , 10) }

→ or Q 11 Q 10 Q 9 Q 8 c 2 c 2 c 2 p y 7 P 11 Q 7 c 1 c 1 c 1 y 6 P 10 Q 6 Probability: 1 − p p y 5 P 9 Q 5 y 4 P 8 Q 4 c 1 → c 1 or c 1 p y 3 P 7 Q 3 y 2 c 2 c 2 c 2 P 6 Q 2 Probability: q p 1 − q p y 1 P 5 Q 1 y j − x i p i , j = P 4 P 3 P 2 P 1 y j − qx i 2 MN pipe dreams − x 1 x 2 x 3 x 4 → n ! permutations For each π ∈ S n , let H π and V π record  1 2 3 4 5 6 7 8 9 10 11  the endpoints of all “horizontal” and π = ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ “vertical” pipes   2 1 3 10 8 6 4 11 5 7 9 Given H , V , let Z H , V ( x , y ) =probability of observing H π = { (6 , 6) , (7 , 4) , (9 , 5) , (10 , 7) } π ∈ S n with H π = H and V π = V . V π = { (4 , 10) }

Flip theorem (G., 2020) Q 11 Q 10 Q 9 Q 8 Q 11 Q 10 Q 9 Q 8 Q 11 Q 10 Q 9 Q 8 Q 11 Q 10 Q 9 Q 8 y 7 y 1 P 11 Q 7 P 11 Q 7 P 11 Q 7 P 11 Q 7 y 6 y 2 P 10 Q 6 P 10 Q 6 P 10 Q 6 P 10 Q 6 y 5 y 3 P 9 Q 5 P 9 Q 5 P 9 Q 5 P 9 Q 5 y 4 y 4 P 8 Q 4 P 8 Q 4 P 8 Q 4 P 8 Q 4 y 3 y 5 P 7 Q 3 P 7 Q 3 P 7 Q 3 P 7 Q 3 y 2 y 6 P 6 Q 2 P 6 Q 2 P 6 Q 2 P 6 Q 2 y 1 y 7 P 5 Q 1 P 5 Q 1 P 5 Q 1 P 5 Q 1 P 4 P 3 P 2 P 1 P 4 P 3 P 2 P 1 P 4 P 3 P 2 P 1 P 4 P 3 P 2 P 1 x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 H π ′ = 180 ◦ ( H ) H π = H Z H , V ( x , y ) = Z 180 ◦ ( H ) , V ( x , rev( y )) V π ′ = V V π = V

→ c 2 c 2 or c 2 p c 1 c 1 c 1 Probability: 1 − p p c 1 → c 1 or c 1 p c 2 c 2 c 2 Probability: q p 1 − q p y j − x i p i , j = y j − qx i Flip theorem: Z H , V ( x , y ) = Z 180 ◦ ( H ) , V ( x , rev( y ))