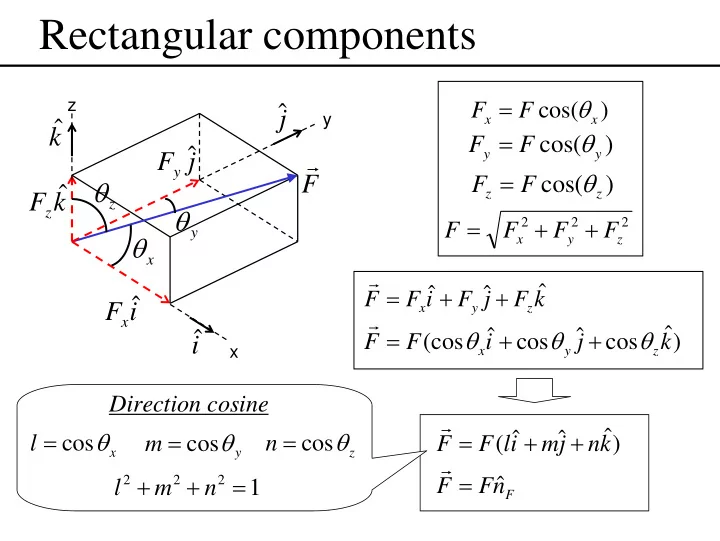

Rectangular components = θ cos( ) ˆ F F z j x x y ˆ k = θ cos( ) F F F y ˆ r y y j = θ cos( ) θ F F F F z ˆ z z k z θ = + + 2 2 2 F F F F y θ x y z x r ˆ = + + ˆ ˆ F F i F j F k F x ˆ i x y z r ˆ = θ + θ + θ ˆ ˆ ˆ (cos cos cos ) F F i j k i x y z x Direction cosine r ˆ = θ = θ = θ = + + ˆ ˆ cos cos cos ( ) l m n F F l i m j n k x y z r = + + = 2 2 2 ˆ 1 F F n l m n F
Writing a vector in 3D (1) 1 Specification by two points on the line of action r r r = = ˆ B ( x 2 , y 2 , z 2 ) AB F F n F z r r F | | r F AB r r r = − A ( x 1 , y 1 , z 1 ) r r r AB B A r y ˆ = + + ˆ ˆ r A x i y j z k x 1 1 1 r ˆ = + + ˆ ˆ r B x i y j z k 2 2 2 r ˆ = − + − + − ˆ ˆ ( ) ( ) ( ) r AB x x i y y j z z k 2 1 2 1 2 1 r ˆ − + − + − ˆ ˆ ( ) ( ) ( ) x x i y y j z z k = 2 1 2 1 2 1 F F − + − + − 2 2 2 ( ) ( ) ( ) x x y y z z 2 1 2 1 2 1
Writing a vector in 3D (2) 2 Specification by two angles which orient the line of action z ˆ ˆ j y k r r r F z = F sin( φ ) F F z F y φ r F xy = F cos( φ ) θ F xy r F x ˆ i x F x = F xy cos( θ ) = F cos( φ ) cos( θ ) F y = F xy sin( θ ) = F cos( φ ) sin( θ )
Dot product r r r P ⋅ = cos( α (scalar) ) P Q PQ r r . Q Projection of in P P cos( α ) α the direction of Q r r Q ˆ ( n ) Q If is a unit vector , dot product r expresses the projection of vector F in the unit vector direction r ˆ ˆ = ⋅ = + + ⋅ α + β + γ ˆ ˆ ˆ ˆ ˆ ( ) ( ) F n F n F l i m j n k i j k r r = ⋅ = α + β + γ ˆ ˆ F n F n n ( ) F l m n r = ⋅ ˆ F n F n r n ˆ ˆ ⋅ = ⋅ = ⋅ = ˆ ˆ ˆ ˆ 1 i i j j k k ˆ ˆ ˆ ˆ ⋅ = ⋅ = ⋅ = ⋅ = ⋅ = ⋅ = ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ 0 i j j i i k k i j k k j
Angle between two vectors r r ⋅ = cos( θ ) P Q PQ From relation of dot product r r The angle between vectors and is Q P r r ⋅ P Q − 1 θ = cos PQ r ˆ The angle between vectors and is n F r ⋅ F ˆ n − θ = cos 1 F r r ˆ = ⋅ n ⊥ 0 ˆ F F n
Sample 1 A force F with a magnitude of 100 N is applied at the origin O of the axes x-y-z as shown. The line of action of F passes through a point A whose coordinates are 3m, 4m and 5m. Determine (a) the x, y and z scalar components of F , (b) the projection F xy of F on the x-y plane, and (c) the projection F OB of F along the line OB.
Sample 2 The cable BC carries a tension of 750 N. Write this tension as a force T acting on point B in terms of the unit vector i , j and k . The elbow at A forms a right angle.
Sample 3 The tension in supporting cable BC is 3200 N. Write the force which this cable exerts on the boom OAB as a vector T . Determine the angles θ x , θ y and θ z which the line of action of T forms with the positive x- , y- and z- axes.
Recommend
More recommend