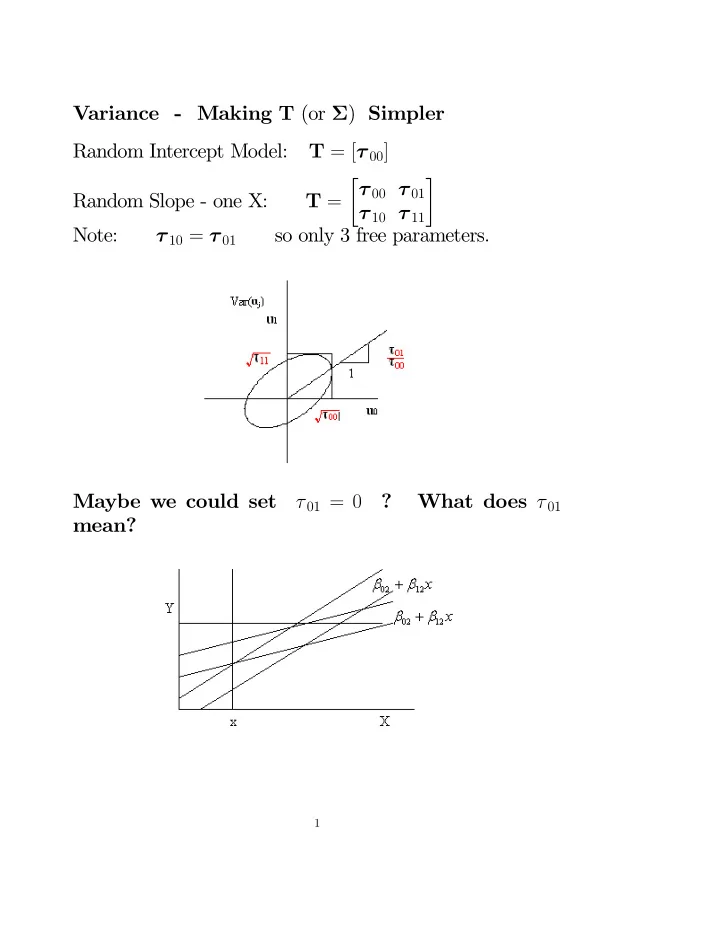
Variance - Making T (or ) Simpler Random Intercept Model: T = [ 00 - PDF document

Variance - Making T (or Σ ) Simpler Random Intercept Model: T = [ τ 00 ] � τ 00 τ 01 � Random Slope - one X: T = τ 10 τ 11 Note: τ 10 = τ 01 so only 3 free parameters. Maybe we could set τ 01 = 0 ? What does τ 01 mean? 1

Consider variance of lines at X : � β 0 � � τ 00 τ 01 � V ar = β 1 τ 10 τ 11 η = β 0 j + β 1 j X � β 0 j � = [1 X ] β 1 j � τ 00 τ 01 � � 1 � V ar ( η ) = [1 X ] X τ 10 τ 11 = τ 00 + 2 τ 01 X + τ 11 X 2 quadratic in X If τ 11 > 0 then quadratic has a minimum at − τ 01 τ 11 • So forcing τ 01 = 0 is equivalent to assuming min SD at X = 0 • This assumption is not invariant if we add a constant to X 2

• Generally arbitrary and not warranted Note: Centering for fixed part or random part or ran- dom part of model? • With OLS, we can make: Cov (ˆ β 0 , ˆ β 1 ) = 0 by centering X at ¯ X • With Mixed Models we can make: � Cov ( β 0 j, β 1 j ) = 0 by centering at τ 01 / ˆ τ 11 doesn’t justify imposing constraint. − ˆ ** BUT often useful to improve convergence. 3

With 2 Random Slopes     β 0 j τ 00 τ 01 τ 02   =   V ar β 1 j τ 10 τ 11 τ 12 β 2 j τ 20 τ 21 τ 22 uncond E ( Y ) = γ 00 + γ 10 X 1 + γ 20 X 2 E ( Y ) ± SD is a bit harder but we can consider contours: 4

X 2 Contours of = SD X 1 Guess shape of contours! � X 1 � � τ 11 τ 12 � − 1 � τ 10 � Note: = X 2 τ 21 τ 22 τ 20 min SD X 2 1 X 1 5

So, τ 12 = 0 < — > Cov ( β 1 j, β 2 j ) = 0 < — > Contour ellipse not tilted And, τ 22 = 0 = > τ 21 = 0 = > Contour horizontal So, in general: 1. Leave τ 01 alone unless you recenter X 1 , X 2 to τ 02 � � X 1 and set them to 0 for numerical reasons. X 2 min SD (Caution: Iterate) 2. τ 12 = 0 might be a legitimate hypothesis. Caution: low power in general so should use a C.I. if "accepting H 0 " (I get better results after centering in (1) but this is numerical) 6

Problem: How to set τ 12 = 0 ? Variance structures and parametrization. What do we know about:   τ 00 τ 01 τ 02   τ 11 τ 12 Note: Only 6 parameters not 9 τ 22 1. τ ii � 0 τ ij 2. ρ ij = √ τ ii √ τ ij Is this enough to be sure that T is a variance matrix? Answer: Yes for 2 x 2 but not enough for larger matrices Variance Matrix should be "positive-definite" — well... at least "non-negative definite" 7

Variance ellipses: Positive Definite Positive Semi Definite degenerate ellipse ρ = ± 1 Positive Semi Definite Positive Semi Definite 8

What if not Non Negative Definite: or even nothing at all (actually: imaginary)! Problem with Mixed Models: Keeping T non negative definite as estimation proceeds. One solution is "Cholesky parametrization" Idea: If T can be expressed in form T = ΛΛ T for some matrix Λ then T is guaranteed to be a variance matrix Lower ∆ Cholesky [What SAS would do with FA0(3)] :   λ 00 0 0   Λ = λ 10 λ 11 0 Note: 6 free parameters λ 20 λ 21 λ 22 9

T = ΛΛ T     λ 00 0 0 λ 00 λ 10 λ 20     = λ 10 λ 11 0 0 λ 11 λ 21 λ 20 λ 21 λ 22 0 0 λ 22   λ 2 λ 00 λ 10 λ 00 λ 20 00 λ 2 10 + λ 2   = 11 λ 10 λ 20 + λ 11 λ 21 λ 2 20 + λ 2 21 + λ 2 22 Note: • Diagonal elements must be � 0 (as expected) • We can force first row of covariances to 0 by forcing λ 10 = λ 20 = 0 other covariances τ 12 = λ 11 λ 21 is not forced to 0. BUT this is NOT what we really want. • We can force first row of covariances to 0 by forcing λ 10 = λ 20 = 0 other covariances τ 12 = λ 11 λ 21 is not forced to 0. • Forcing λ 21 = 0 does not force τ 12 = 0 SAS Trick: • Put intercept last in RANDOM statement. Then you can use PARMS to force λ 21 = 0 and τ 12 will be 0. T will be: 10

    λ 2 β 1 j λ 11 λ 21 λ 11 λ 01 11 λ 2 21 + λ 2   =   V ar β 2 j 22 λ 21 λ 01 + λ 22 λ 02 λ 2 01 + λ 2 02 + λ 2 β 0 j 00 So we can constrain τ 12 = 0 by constrainng λ 21 = 0 In SAS RANDOM X1 X2 INTERCEPT / TYPE = FA0(3) SUB = ID G GC GCORR; PARMS (1) (0) (0.5) (0.021) (-0.03 (0.01) / HOLD = 2; Note: Fill in values from previous run or make good guess Note: S-Plus LME uses log Cholesky   e θ 0 0 0  λ 10 e θ 1  0 parameters: θ 1 , θ 2 , θ 3 , λ 10 , λ 20 λ 21 e θ 2 λ 20 , λ 21 Which is an unconstrained parametrization of PD matrices. Default parametrization in SAS: TYPE = VC is diagonal 11

  0 0 τ 00   0 0 Which violates " τ ok " τ 11 0 0 τ 22 principle Some other SAS parametrizations Unstructured - anything ... not necessarily a TYPE = UN vanance matrix TYPE = AR (1)   ρ ρ 2 ρ 3 1   ρ ρ 2 ρ 1   useful for for R ( Σ ) matrix for ρ 2 ρ   1 ρ ρ 3 ρ 2 ρ 1 longitudinal data TYPE = UN (1) . . . See PROC MIXED p 2002 ff. Many of these will be more useful for longitudinal models. • I would like to have Block Diagonal for variables other than intercept and anything for cov with intercept, e.g: 12

— Consider:   τ 11 τ 12 τ 13 τ 10   τ 21 τ 22 τ 23 τ 20     τ 31 τ 32 τ 33 τ 30 τ 01 τ 02 τ 03 τ 00 — Would like:   0 τ 11 τ 12 τ 10   0 τ 21 τ 22 τ 20     0 0 τ 33 τ 30 τ 01 τ 02 τ 03 τ 00 — Can get this with Λ :   λ 11 0 0 0   λ 21 λ 22 0 0     0 0 λ 33 0 λ 01 λ 02 λ 03 λ 00 — Block diagonal structure in upper left square parti- tion of Λ is reproduced in T — So we can do this with PARMS by forcing upper-left elements of Λ to be 0 • Why this particular structure? — If X 1 , X 2 are dummy variables for a 3-level cate- gorical variable it generally does not make sense to require τ 12 = 0 (not invariant w.r.t. recoding). But it does makes sense to ask whether the effect of the categorical variable is independent of X 3 13

Note: that for PROC NLMIXED you can do Cholesky by hand. So might as well use log-Cholesky 14

Tests and C.I.’s for T (Σ) Wald, Wilks and Fisher OR - How far are we from the summit? Note: curvature of log-likelihood = "info" • For τ ij ( i � = j ) we can test τ ij = 0 with a valid test • More problematic for τ ii = 0 since τ ii can not be < 0 • If Ho : τ ii = 0 and no other covariances are implied some advocate x p-value by 2. • If we are also dropping covariances, we could use simu- lation - but probably not in SAS 15

• Bates & Pinheiro throw up their hands and use regular p taking comfort from fact that the error is "conservative" - but NOT if you are going to accept Ho!! 16