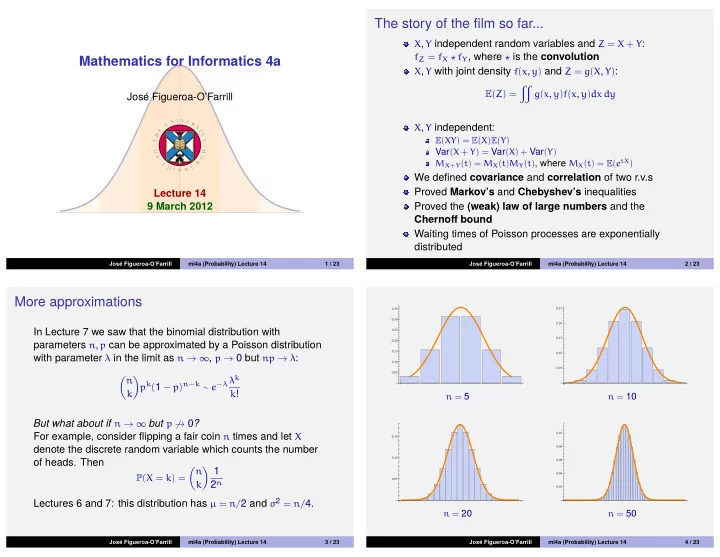

The story of the film so far... X , Y independent random variables and Z = X + Y : f Z = f X ⋆ f Y , where ⋆ is the convolution Mathematics for Informatics 4a X , Y with joint density f ( x , y ) and Z = g ( X , Y ) : � E ( Z ) = g ( x , y ) f ( x , y ) dx dy Jos´ e Figueroa-O’Farrill X , Y independent: E ( XY ) = E ( X ) E ( Y ) Var ( X + Y ) = Var ( X ) + Var ( Y ) M X + Y ( t ) = M X ( t ) M Y ( t ) , where M X ( t ) = E ( e tX ) We defined covariance and correlation of two r.v.s Proved Markov’s and Chebyshev’s inequalities Lecture 14 9 March 2012 Proved the (weak) law of large numbers and the Chernoff bound Waiting times of Poisson processes are exponentially distributed Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 1 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 2 / 23 More approximations 0.25 0.35 0.30 0.20 In Lecture 7 we saw that the binomial distribution with 0.25 0.15 0.20 parameters n , p can be approximated by a Poisson distribution 0.15 0.10 with parameter λ in the limit as n → ∞ , p → 0 but np → λ : 0.10 0.05 0.05 p k ( 1 − p ) n − k ∼ e − λ λ k � n � k k ! n = 5 n = 10 But what about if n → ∞ but p �→ 0 ? 0.10 For example, consider flipping a fair coin n times and let X 0.15 denote the discrete random variable which counts the number 0.08 0.10 of heads. Then 0.06 � 1 � n 0.04 P ( X = k ) = 0.05 2 n k 0.02 Lectures 6 and 7: this distribution has µ = n/ 2 and σ 2 = n/ 4. n = 20 n = 50 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 3 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 4 / 23
Normal limit of (symmetric) binomial distribution Proof Theorem Let k = n 2 + x . Then Let X be binomial with parameter n and p = 1 2 . Then for n large n !2 − n � n � � n � 2 − n = 2 − n = and k − n/ 2 not too large, � n � n n � ! � ! k 2 + x 2 + x 2 − x � 1 � n � n � 1 2 n � n e −( k − µ ) 2 / 2 σ 2 = n !2 − n � � 2 − 1 · · · 2 − ( x − 1 ) nπe − 2 ( k − n/ 2 ) 2 /n √ 2 2 n ≃ = � ! × � n � n � n � � n � n k 2 πσ � ! � � 2 + 1 2 + 2 2 + x · · · 2 2 � � n � � � � x for µ = n/ 2 and σ 2 = n/ 4 . 1 − 2 1 − ( x − 1 ) 2 1 � · · · 2 n n 2 ≃ nπ × � � n � � � � � � x 1 + 2 1 + 2 2 1 + x 2 · · · The proof rests on the de Moivre/Stirling formula for the factorial n n n 2 of a large number: Now we use the exponential approximation √ 2 πn n √ ne − n n ! ≃ 1 1 − z ≃ e − z 1 + z ≃ e − z and which implies that � n � � n ! 2 ( n/ 2 ) ! ( n/ 2 ) ! ≃ 2 n = (valid for z small) to rewrite the big fraction in the RHS. n/ 2 πn Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 5 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 6 / 23 Proof – continued. Example (Rolling a die ad nauseam ) It’s raining outside, you are bored and you roll a fair die 12000 � � n � 2 � − 4 n − 8 n − · · · − 2 ( x − 1 ) − 2 x � times. Let X be the number of sixes. What is 2 − n ≃ nπ exp P ( 1900 < X < 2200 ) ? k n n The variable X is the sum X 1 + · · · + X 12000 , where X i is the � 2 � − 4 n ( 1 + 2 + · · · + ( x − 1 )) − 2 x � nπ exp = number of sixes on the i th roll. This means that X is binomially n distributed with parameter n = 12000 and p = 1 6 , so � 2 � − 4 x ( x − 1 ) − 2 x � µ = pn = 2000 and σ 2 = np ( 1 − p ) = 5000 3 . = nπ exp √ √ 2 n n X ∈ ( 1900, 2200 ) iff X − 2000 ∈ (− 6, 2 6 ) , whence σ � 2 nπe − 2 x 2 /n √ √ = P ( 1900 < X < 2200 ) ≃ Φ ( 2 6 ) − Φ (− 6 ) ≃ 0.992847 which is indeed a normal distribution with σ 2 = n 4 . The exact result is 2199 A similar proof shows that the general binomial distribution with � 12000 � � � 12000 − k � � k � 1 5 µ = np and σ 2 = np ( 1 − p ) is also approximated by a normal ≃ 0.992877 6 6 k distribution with the same µ and σ 2 . k = 1901 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 7 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 8 / 23
Normal limit of Poisson distribution We have just shown that in certain limits of the defining parameters, two discrete probability distributions tend to normal distributions: 0.12 the binomial distribution in the limit n → ∞ , 0.15 0.10 the Poisson distribution in the limit λ → ∞ 0.08 0.10 0.06 What about continuous probability distributions? 0.04 0.05 We could try with the uniform or exponential distributions: 0.02 λ = 5 λ = 10 1.0 4 0.8 3 0.6 0.08 0.05 2 0.4 0.04 0.06 1 0.2 0.03 0.04 0.02 � 1 1 2 3 4 0.5 1.0 1.5 2.0 2.5 3.0 0.02 No amount of rescaling is going to work. Why? 0.01 λ = 20 λ = 50 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 9 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 10 / 23 The binomial and Poisson distributions have the following Sum of uniformly distributed variables property: X i i.i.d. uniformly distributed on [ 0, 1 ] : then X 1 + · · · + X n is if X , Y are binomially distributed with parameters ( n , p ) and ( m , p ) , X + Y is binomially distributed with parameter 1.4 1.0 ( n + m , p ) 1.2 0.8 1.0 if X , Y are Poisson distributed with parameters λ and µ , 0.6 0.8 X + Y is Poisson distributed with parameter λ + µ 0.6 0.4 0.4 It follows that if X 1 , X 2 , . . . are i.i.d. with binomial 0.2 0.2 distribution with parameters ( m , p ) , X 1 + · · · + X n is � 1 1 2 3 � 1.0 � 0.5 0.5 1.0 1.5 2.0 binomial with parameter ( nm , p ) . Therefore m large is n = 1 n = 2 equivalent to adding many of the X i . It also follows that if X 1 , X 2 , . . . are i.i.d. with Poisson 0.7 0.8 0.6 distribution with parameter λ , X 1 + · · · + X n is Poisson 0.6 0.5 distributed with parameter nλ and again λ large is 0.4 0.4 equivalent to adding a large number of the X i . 0.3 0.2 0.2 The situation with the uniform and exponential distributions 0.1 � 1 1 2 3 4 � 1 1 2 3 4 5 is different. n = 3 n = 4 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 11 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 12 / 23
Sum of exponentially distributed variables 0.12 If X i are i.i.d. exponentially distributed with parameter λ , we 0.15 0.10 already saw that Z 2 = X 1 + X 2 has a “gamma” probability 0.08 density function: 0.10 0.06 f Z 2 ( z ) = λ 2 ze − λz 0.04 0.05 0.02 2 4 6 8 10 5 10 15 20 It is not hard to show that Z n = X 1 + · · · + X n has probability n = 5 n = 10 density function z n − 1 f Z n ( z ) = λ n ( n − 1 ) ! e − λz 0.08 0.04 0.06 0.03 0.04 0.02 What happens when we take n large? 0.02 0.01 10 20 30 40 20 40 60 80 100 120 140 n = 20 n = 75 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 13 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 14 / 23 The Central Limit Theorem Our 4-line proof of the CLT rests on L´ evy’s continuity law , which we will not prove. Let X 1 , X 2 , . . . be i.i.d. random variables with mean µ and Paraphrasing: “the m.g.f. determines the c.d.f.” variance σ 2 . It is then enough to show that the limit n → ∞ of the m.g.f. Let Z n = X 1 + · · · + X n . of Z n − nµ is the m.g.f. of the standard normal distribution. Then Z n has mean nµ and variance nσ 2 , but in addition we √ nσ have Proof of CLT. Theorem (Central Limit Theorem) We shift the mean: the variables Y i = X i − µ are i.i.d. with mean 0 and variance σ 2 , and Z n − nµ = Y 1 + · · · + Y n . In the limit as n → ∞ , M Z n − nµ ( t ) = M Y 1 ( t ) · · · M Y n ( t ) = M Y 1 ( t ) n , by i.i.d. � Z n − nµ � √ nσ � n P � x → Φ ( x ) � � � t t M Zn − nµ √ nσ ( t ) = M Z n − nµ = M Y 1 √ nσ √ nσ � n � 1 + σ 2 t 2 → e t 2 / 2 , which is the m.g.f. with Φ the c.d.f. of the standard normal distribution. M Zn − nµ √ nσ ( t ) = 2 nσ 2 + · · · of a standard normal variable. In other words, for n large, Z n is normally distributed. Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 15 / 23 Jos´ e Figueroa-O’Farrill mi4a (Probability) Lecture 14 16 / 23
Recommend
More recommend