Safety Problems are NP-complete for Flat Integer Programs with - PowerPoint PPT Presentation

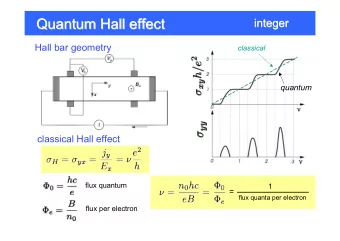
Safety Problems are NP-complete for Flat Integer Programs with Octagonal Loops Marius Bozga, Radu Iosif (Verimag/CNRS, France) Filip Konecny (EPFL, Switzerland)

Motivation • Infinite state systems are, in general, undecidable • Few complexity results for the decidable cases: VAS coverage (EXPSPACE-complete) [Rackoff 1978] ➡ inequivalence of reversal-bounded CM (NP-complete) [Ibarra, Gurari 1981] ➡ gap-order constraints (PSPACE-complete) [Bozzelli, Pinchinat 2012] ➡ • Efficient algorithm for flat integer programs with difference bounds and octagonal loops [BIK’10] worst case EXPTIME, yet good average performance ➡ • NP-completness explains the behavior of our algorithm educated guessing may solve NP-complete problems efficiently ➡

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x ++; y ++; } else { x ++; y --; }} assert(y == y0);

Flat Integer Programs y int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x ++; y ++; } else { x ++; y --; }} y 0 assert(y == y0); x 0 m n x

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x ++; y ++; } else { x ++; y --; }} assert(y == y0);

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x < n x’=x+1 x < n x’=x+1 x ++; x < m y’=y+1 x ≥ m y’=y-1 y ++; } else { y’=y0 x ++; y ≠ y0 n’=2*m-x y --; }} assert(y == y0);

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x < n x’=x+1 x < n x’=x+1 x ++; x < m y’=y+1 x ≥ m y’=y-1 y ++; } else { y’=y0 x ++; y ≠ y0 n’=2*m-x y --; { }} x 1 -x 0= y 1 -y 0= m-x 0 assert(y == y0);

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x < n x’=x+1 x < n x’=x+1 x ++; x < m y’=y+1 x ≥ m y’=y-1 y ++; } else { y’=y0 x ++; y ≠ y0 n’=2*m-x y --; { { }} x 1 -x 0= y 1 -y 0= m-x 0 x 2 -x 1= y 1 -y 2= n-m assert(y == y0);

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x < n x’=x+1 x < n x’=x+1 x ++; x < m y’=y+1 x ≥ m y’=y-1 y ++; } else { y’=y0 x ++; y ≠ y0 n’=2*m-x y --; { { }} x 1 -x 0= y 1 -y 0= m-x 0 x 2 -x 1= y 1 -y 2= n-m assert(y == y0); { y 1 -y 0= y 1 -y 2

Flat Integer Programs int y = y0; int n = 2*m - x; while (x < n) { if (x < m) { x < n x’=x+1 x < n x’=x+1 x ++; x < m y’=y+1 x ≥ m y’=y-1 y ++; } else { y’=y0 x ++; y ≠ y0 n’=2*m-x y --; { { }} x 1 -x 0= y 1 -y 0= m-x 0 x 2 -x 1= y 1 -y 2= n-m assert(y == y0); { y 1 -y 0= y 1 -y 2 y 0= y 2

Flat Integer Programs • Reachability is decidable if the relations labeling the loops belong to certain classes of linear inequalities • Difference bounds constraints: 3 ≤ x ≤ 5 /\ 1 ≤ y ≤ 3 /\ 2 ≤ x - y ≤ 4

Flat Integer Programs • Reachability is decidable if the relations labeling the loops belong to certain classes of linear inequalities • Difference bounds constraints: 3 ≤ x ≤ 5 /\ 1 ≤ y ≤ 3 /\ 2 ≤ x - y ≤ 4 y 3 1 3 5 x

Flat Integer Programs • Reachability is decidable if the relations labeling the loops belong to certain classes of linear inequalities • Octagonal constraints: 4 ≤ x ≤ 6 /\ 1 ≤ y ≤ 3 /\ 0 ≤ x - y ≤ 5 /\ 5 ≤ x + y ≤ 7

Flat Integer Programs • Reachability is decidable if the relations labeling the loops belong to certain classes of linear inequalities • Octagonal constraints: 4 ≤ x ≤ 6 /\ 1 ≤ y ≤ 3 /\ 0 ≤ x - y ≤ 5 /\ 5 ≤ x + y ≤ 7 y 3 1 4 5 6 7 x

Difference Bounds Relations x 1 ′ x 1 x 2 x 2 ′

Difference Bounds Relations 1 x 1 ′ x 1 - x 1 ′ ≤ 1 x 1 x 2 x 2 ′

Difference Bounds Relations 1 x 1 ′ x 1 - x 1 ′ ≤ 1 x 1 x 1 - x 2 ′ ≤ -1 -1 x 2 x 2 ′

Difference Bounds Relations 1 x 1 ′ x 1 - x 1 ′ ≤ 1 x 1 x 1 - x 2 ′ ≤ -1 -1 -2 x 2 - x 1 ′ ≤ -2 x 2 x 2 ′

Difference Bounds Relations 1 x 1 ′ x 1 - x 1 ′ ≤ 1 x 1 x 1 - x 2 ′ ≤ -1 -1 -2 x 2 - x 1 ′ ≤ -2 2 x 2 - x 2 ′ ≤ 2 x 2 x 2 ′

Difference Bounds Relations x 1 x 2 x 1 ′ x 2 ′ 1 x 1 ′ x 1 - x 1 ′ ≤ 1 x 1 x 1 0 ∞ 1 -1 x 1 - x 2 ′ ≤ -1 -1 -2 x 2 ∞ 0 -2 2 x 2 - x 1 ′ ≤ -2 x 1 ′ ∞ ∞ 0 ∞ 2 x 2 - x 2 ′ ≤ 2 x 2 x 2 ′ x 2 ′ ∞ ∞ ∞ 0

Difference Bounds Relations 1 x 1 ′ x 1 -1 -2 2 x 2 x 2 ′

Difference Bounds Relations 1 1 x 1 ′ x 1 ′′ x 1 -1 -2 -1 -2 2 2 x 2 x 2 ′ x 2 ′′

Difference Bounds Relations 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1 -1 -2 -1 -2 -1 -2 2 2 2 x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 -1 -2 -1 -2 -1 -2 -1 -2 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 x 1 - x 1iv ≤ -6 -1 -2 -1 -2 -1 -2 -1 -2 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 x 1 - x 1iv ≤ -6 -1 -2 -1 -2 -1 -2 -1 -2 x 1 - x 2iv ≤ -2 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 x 1 - x 1iv ≤ -6 -1 -2 -1 -2 -1 -2 -1 -2 x 1 - x 2iv ≤ -2 x 2 - x 1iv ≤ -4 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 x 1 - x 1iv ≤ -6 -1 -2 -1 -2 -1 -2 -1 -2 x 1 - x 2iv ≤ -2 x 2 - x 1iv ≤ -4 x 2 - x 2iv ≤ -6 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 x 1 - x 1iv ≤ -6 -1 -2 -1 -2 -1 -2 -1 -2 x 1 - x 2iv ≤ -2 x 2 - x 1iv ≤ -4 x 2 - x 2iv ≤ -6 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′

Difference Bounds Relations 1 1 1 1 x 1 ′ x 1 ′′ x 1 ′′′ x 1iv x 1 x 1 - x 1iv ≤ -6 -1 -2 -1 -2 -1 -2 -1 -2 x 1 - x 2iv ≤ -2 x 2 - x 1iv ≤ -4 x 2 - x 2iv ≤ -6 2 2 2 2 x 2iv x 2 x 2 ′ x 2 ′′ x 2 ′′′ • The n-th power of a DB relation is again a DB relation: ➡ the class of DB has quantifier elimination • We are interested in computing minimal weight paths • The graph for the n-th power has (n+1) × (#vars) nodes • The paths in the graph are regular

Difference Bounds Relations x 1 - x 2 ′ ≤ 0 x 1 x 1 ′ x 2 - x 3 ′ ≤ 0 x 2 x 2 ′ x 3 ′ - x 2 ≤ 0 x 4 ′ - x 5 ≤ 0 x 3 x 3 ′ x 5 ′ - x 6 ≤ 0 x 4 x 4 ′ x 6 ′ - x 6 ≤ 1 x 6 ′ - x 7 ≤ 0 x 5 x 5 ′ x 7 - x 7 ′ ≤ 1 x 6 x 6 ′ x 7 ′ - x 5 ≤ 0 x 5 - x 1 ′ ≤ -1 x 7 x 7 ′

Difference Bounds Relations x 1 x 1 ′ x 2 x 2 ′ x 3 x 3 ′ x 4 x 4 ′ x 5 x 5 ′ x 6 x 6 ′ x 7 x 7 ′

Difference Bounds Relations x 1 x 1 ′ x 2 x 2 ′ x 3 x 3 ′ x 4 x 4 ′ x 5 x 5 ′ x 6 x 6 ′ x 7 x 7 ′

Difference Bounds Relations γ 0 γ 1 γ 1 γ 2 γ 3 γ 4 γ 5 γ 6 γ 7 γ 8 γ 9 γ 2 γ 3 γ 4 x 1 x 1 ′ x 2 x 2 ′ x 3 x 3 ′ x 4 x 4 ′ x 5 x 5 ′ x 6 x 6 ′ x 7 x 7 ′

Difference Bounds Relations γ 0 γ 1 γ 1 γ 2 γ 3 γ 4 γ 5 γ 6 γ 7 γ 8 γ 9 γ 2 γ 3 γ 4

Difference Bounds Relations γ 0 γ 1 γ 1 γ 2 γ 3 γ 4 γ 5 γ 6 γ 7 γ 8 γ 9 γ 2 γ 3 γ 4 → → → → → → → → → → → → → → → → → → → → ‹ ‹ ‹ ‹ ‹ ‹ ‹ ‹ ‹ → → → → → → → → → → ‹ ‹ ‹ ‹ ‹ ‹ ‹ ‹ ‹ → → → → → → ‹ ‹ → → → → → → → → → → → → q 0 q 1 q 2 q 2 q 3 q 4 q 5 q 7 q 8 q 9 q 10 q 2 q 3 q 4 q 5

Zigzag Automata γ 1 (1) γ 0 (0) γ 1 (1) γ 2 (0) γ 3 (1) γ 4 (1) → q 0 q 1 q 2 q 3 q 4 q 5 γ 5 (1) γ 5 (1) γ 5 (1) γ 9 (0) q 6 γ 8 (-1) γ 7 (-1) γ 6 (0) γ 5 (1) q 10 q 9 q 8 q 7 γ 8 (-1)

Zigzag Automata γ 1 (1) γ 0 (0) γ 1 (1) γ 2 (0) γ 3 (1) γ 4 (1) → q 0 q 1 q 2 q 3 q 4 q 5 γ 5 (1) γ 5 (1) γ 5 (1) γ 9 (0) q 6 γ 8 (-1) γ 7 (-1) γ 6 (0) γ 5 (1) q 10 q 9 q 8 q 7 γ 8 (-1) • All paths in the n-th unfolding of the constraint graph are encoded as runs of weighted automata [BIL’06] • Minimal weight paths become minimal weight runs

Zigzag Automata γ 1 (1) γ 0 (0) γ 1 (1) γ 2 (0) γ 3 (1) γ 4 (1) → q 0 q 1 q 2 q 3 q 4 q 5 γ 5 (1) γ 5 (1) γ 5 (1) γ 9 (0) q 6 γ 8 (-1) γ 7 (-1) γ 6 (0) γ 5 (1) q 10 q 9 q 8 q 7 γ 8 (-1)

Zigzag Automata γ 1 (1) γ 0 (0) γ 1 (1) γ 2 (0) γ 3 (1) γ 4 (1) → q 0 q 1 q 2 q 3 q 4 q 5 γ 5 (1) γ 5 (1) γ 5 (1) γ 9 (0) q 6 γ 8 (-1) γ 7 (-1) γ 6 (0) γ 5 (1) q 10 q 9 q 8 q 7 γ 8 (-1) • We compute a function on the automaton: min_weight A (n) ¡= ¡min{ω(ρ) ¡| ¡ρ ¡is ¡a ¡run ¡of ¡A, ¡|ρ|=n} • Minimal weight functions are periodic [deSchutter’00] ➡ mininal weight runs iterate through critical cycles

Zigzag Automata γ 1 (1) γ 0 (0) γ 1 (1) γ 2 (0) γ 3 (1) γ 4 (1) → q 0 q 1 q 3 q 4 q 5 q 2 γ 5 (1) γ 5 (1) γ 5 (1) γ 9 (0) q 6 γ 8 (-1) γ 7 (-1) γ 6 (0) γ 5 (1) q 10 q 9 q 8 q 7 γ 8 (-1) ϖ( γ 1* ) = ω ( γ 1 ) / | γ 1 | = 1