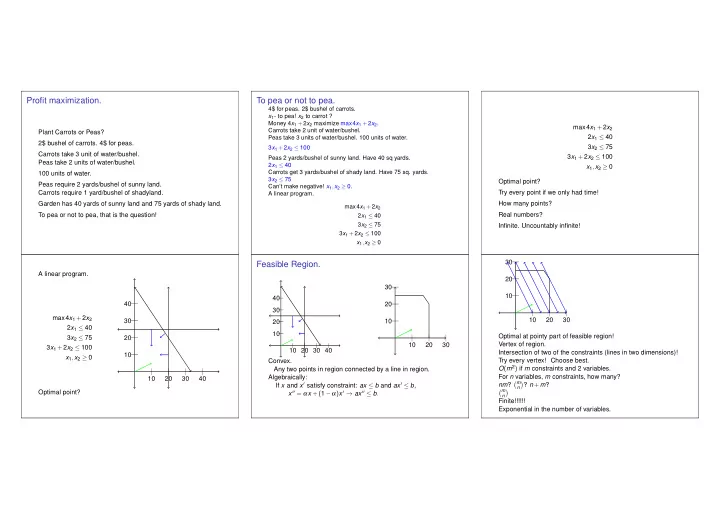
Profit maximization. To pea or not to pea. 4$ for peas. 2$ bushel - PowerPoint PPT Presentation

Profit maximization. To pea or not to pea. 4$ for peas. 2$ bushel of carrots. x 1 - to pea! x 2 to carrot ? Money 4 x 1 + 2 x 2 maximize max4 x 1 + 2 x 2 . max4 x 1 + 2 x 2 Carrots take 2 unit of water/bushel. Plant Carrots or Peas? 2 x 1 ≤ 40 Peas take 3 units of water/bushel. 100 units of water. 2$ bushel of carrots. 4$ for peas. 3 x 2 ≤ 75 3 x 1 + 2 x 2 ≤ 100 Carrots take 3 unit of water/bushel. 3 x 1 + 2 x 2 ≤ 100 Peas 2 yards/bushel of sunny land. Have 40 sq yards. Peas take 2 units of water/bushel. 2 x 1 ≤ 40 x 1 , x 2 ≥ 0 Carrots get 3 yards/bushel of shady land. Have 75 sq. yards. 100 units of water. 3 x 2 ≤ 75 Optimal point? Peas require 2 yards/bushel of sunny land. Can’t make negative! x 1 , x 2 ≥ 0. Carrots require 1 yard/bushel of shadyland. Try every point if we only had time! A linear program. Garden has 40 yards of sunny land and 75 yards of shady land. How many points? max4 x 1 + 2 x 2 To pea or not to pea, that is the question! Real numbers? 2 x 1 ≤ 40 3 x 2 ≤ 75 Infinite. Uncountably infinite! 3 x 1 + 2 x 2 ≤ 100 x 1 , x 2 ≥ 0 30 Feasible Region. A linear program. 20 30 10 40 40 20 30 max4 x 1 + 2 x 2 10 20 30 30 10 20 2 x 1 ≤ 40 10 Optimal at pointy part of feasible region! 3 x 2 ≤ 75 20 10 20 30 Vertex of region. 3 x 1 + 2 x 2 ≤ 100 10 20 30 40 Intersection of two of the constraints (lines in two dimensions)! 10 x 1 , x 2 ≥ 0 Try every vertex! Choose best. Convex. O ( m 2 ) if m constraints and 2 variables. Any two points in region connected by a line in region. For n variables, m constraints, how many? Algebraically: 10 20 30 40 If x and x ′ satisfy constraint: ax ≤ b and ax ′ ≤ b , � m � nm ? ? n + m ? n x ′′ = α x +( 1 − α ) x ′ → ax ′′ ≤ b . � m Optimal point? � n Finite!!!!!! Exponential in the number of variables.

30 Duality. Duality. max x 1 + 8 x 2 max4 x 1 + 2 x 2 20 max x 1 + 8 x 2 2 x 1 ≤ 40 x 1 ≤ 4 x 1 ≤ 4 10 3 x 2 ≤ 75 x 2 ≤ 3 x 2 ≤ 3 3 x 1 + 2 x 2 ≤ 100 x 1 + 2 x 2 ≤ 7 x 1 + 2 x 2 ≤ 7 x 1 , x 2 ≥ 0 x 1 , x 2 ≥ 0 x 1 , x 2 ≥ 0 10 20 30 Simplex: Start at vertex. Move to better neighboring vertex. One Solution: x 1 = 1 , x 2 = 3 . Value is 25. Solution value: 25. Until no better neighbor. This example. Add equation 1 and 8 times equation 2 gives.. (0,0) objective 0. → ( 0 , 25 ) objective 50. Best possible? x 1 + 8 x 2 ≤ 4 + 24 = 28. → ( 16 2 3 , 25 ) objective 115 2 3 For any solution. → ( 20 , 20 ) objective 120. Better way to add equations to get bound on function? x 1 ≤ 4 and x 2 ≤ 3 .. Duality: Sure: 6 times equation 2 and 1 times equation 3. ....so x 1 + 8 x 2 ≤ 4 + 8 ( 3 ) = 28 . Add blue equations to get objective function? x 1 + 8 x 2 ≤ 6 ( 3 )+ 7 = 25 . Added equation 1 and 8 times equation 2 1 / 2 times first plus second. Get 4 x 1 + 2 x 2 ≤ 120. Every solution must satisfy this inequality! Thus, the value is at most 25. yields bound on objective.. Objective value: 120. Better solution? The upper bound is same as solution! Can we do better? No! Better upper bound? Dual problem: add equations to get best upper bound. Proof of optimality! Duality:example Duality: computing upper bound. The dual, the dual, the dual. Find best y i ’s to minimize upper bound? Best Upper Bound. Again: If you find y 1 , y 2 , y 3 ≥ 0 and y 1 + y 3 ≥ 1 and y 2 + 2 y 3 ≥ 8 then.. Multiplier Inequality x 1 + 8 x 2 ≤ 4 y 1 + 3 y 2 + 7 y 3 y 1 x 1 ≤ 4 min 4 y 1 + 3 y 2 + 7 y 3 Idea: Add up positive linear combination of inequalities to “get” y 2 x 2 ≤ 3 y 1 + y 3 ≥ 1 upper bound on optimization function. y 2 + 2 y 3 ≥ 8 y 3 x 1 + 2 x 2 ≤ 7 Will this always work? y 1 , y 2 , y 3 ≥ 0 Adding equations thusly... How to find best upper bound? ( y 1 + y 3 ) x 1 +( y 2 + 2 y 3 ) x 2 ≤ 4 y 1 + 3 y 2 + 7 y 3 . The left hand side should “dominate” optimization function: A linear program. If y 1 , y 2 , y 3 ≥ 0 The Dual linear program. and y 1 + y 3 ≥ 1 and y 2 + 2 y 3 ≥ 8 then.. x 1 + 8 x 2 ≤ 4 y 1 + 3 y 2 + 7 y 3 Primal: ( x 1 , x 2 ) = ( 1 , 3 ) ; Dual: ( y 1 , y 2 , y 3 ) = ( 0 , 6 , 1 ) . Find best y i ’s to minimize upper bound? Value of both is 25! Primal is optimal ... and dual is optimal!

The dual. Complementary Slackness Again: simplex In general. 30 Primal LP Dual LP min y T b max c · x max4 x 1 + 2 x 2 20 y T A ≥ c Primal LP Dual LP 3 x 1 ≤ 60 Ax ≤ b min y T b 10 3 x 2 ≤ 75 max c · x x ≥ 0 y ≥ 0 y T A ≥ c 3 x 1 + 2 x 2 ≤ 100 Ax ≤ b Given A , b , c , and feasible solutions x and y . 10 20 30 x 1 , x 2 ≥ 0 x ≥ 0 y ≥ 0 Solutions x and y are both optimal if and only if Simplex: Start at vertex. Move to better neighboring vertex. x i ( c i − ( y T A ) i ) = 0, and y j ( b j − ( Ax ) j ) . Theorem: If a linear program has a bounded value, then its dual is Until no better neighbor. Duality: x i ( c i − ( y T A ) i ) = 0 → bounded and has the same value. Add blue equations to get objective function? ∑ i ( c i − ( y T A ) i ) x i = cx − y T Ax → cx = y T Ax . 1 / 3 times first plus second. Weak Duality: primal ( P ) ≤ dual ( D ) Get 4 x 1 + 2 x 2 ≤ 120. Every solution must satisfy this inequality! y j ( b j − ( Ax ) j ) = 0 → Feasible ( x , y ) Geometrically and Complementary slackness: ∑ i y j ( b j − ( Ax ) j ) = yb − y T Ax → by = y T Ax . P ( x ) = c · x ≤ y T Ax ≤ y T b · x = D ( y ) . Add tight constraints to “dominate objective function.” cx = by . Don’t add this equation! Shifts. Strong Duality: next lecture, previous lectures maybe? If both are feasible, cx ≤ by , so must be optimal. In words: nonzero dual variables only for tight constraints! Example: review. Matrix equations. Rules for School... or...”Rules for taking duals” Canonical Form. max x 1 + 8 x 2 min 4 y 1 + 3 y 2 + 7 y 3 max [ 1 , 8 ] · [ x 1 , x 2 ] min [ 4 , 3 , 7 ] · [ y 1 , y 2 , y 3 ] x 1 ≤ 4 y 1 + y 3 ≥ 1  1 0   4   1 0  Primal LP Dual LP � x 1 � � 1 � x 2 ≤ 3 y 2 + 2 y 3 ≥ 8  ≥ min y T b 0 1 ≤ 3 [ y 1 , y 2 , y 3 ] 0 1 max c · x      8 x 2 x 1 + 2 x 2 ≤ 7 x 1 , x 2 ≥ 0 1 2 7 1 2 y T A ≥ c Ax ≤ b y 1 , y 2 , y 3 ≥ 0 [ x 1 , x 2 ] ≥ 0 [ y 1 , y 2 , y 3 ] ≥ 0 x ≥ 0 y ≥ 0 “Matrix form” Standard: We can rewrite the above in matrix form. Ax ≤ b , max cx , x ≥ 0 ↔ y T A ≥ c , min by , y ≥ 0. max [ 1 , 8 ] · [ x 1 , x 2 ] min [ 4 , 3 , 7 ] · [ y 1 , y 2 , y 3 ] min ↔ max  1 0   4   1 0  � x 1 � � 1 �   1 0  ≥ 0 1 3 [ y 1 , y 2 , y 3 ] 0 1 ≤ ≥↔≤      x 2 8 A = 0 1 c = [ 1 , 8 ] b = [ 4 , 3 , 7 ] 1 2 7 1 2   “inequalities” ↔ “nonnegative variables” 1 2 [ x 1 , x 2 ] ≥ 0 [ y 1 , y 2 , y 3 ] ≥ 0 “nonnegative variables” ↔ “inequalities” The primal is Ax ≤ b , max c · x , x ≥ 0. Another useful trick: Equality constraints. “equalities” ↔ The dual is y T A ≥ c , min b · y , y ≥ 0. “unrestricted variables.”