Physics 2D Lecture Slides Lecture 24: Mar 1 st Vivek Sharma UCSD - PDF document

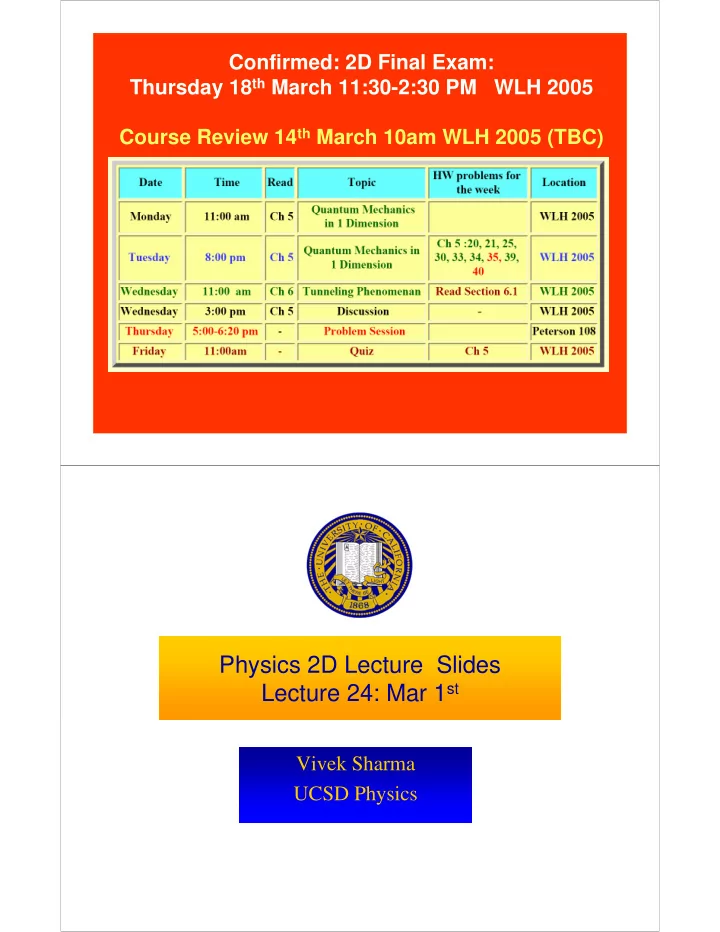
Confirmed: 2D Final Exam: Thursday 18 th March 11:30-2:30 PM WLH 2005 Course Review 14 th March 10am WLH 2005 (TBC) Physics 2D Lecture Slides Lecture 24: Mar 1 st Vivek Sharma UCSD Physics

Quiz 7 20 Frequency 15 10 5 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Grades Common mistakes: 1. Needed to translate x � x+ L/2 2. Difference between probability and probability amplitude ! 3. For photon, using E = P 2 /2m is a very bad idea Finite Potential Barrier • There are no Infinite Potentials in the real world – Imagine the cost of as battery with infinite potential diff • Will cost infinite $ sum + not available at Radio Shack • Imagine a realistic potential : Large U compared to KE but not infinite Region III Region II Region I U E=KE X=L X=0 Classical Picture : A bound particle (no escape) in 0 < x < L Quantum Mechanical Picture : Use ∆ E. ∆ t ≤ h/2 π Particle can leak out of the Box of finite potential P(|x|>L) ≠ 0

Finite Potential Well ψ � 2 2 - ( ) d x + ψ = ψ U ( ) x E ( ) x 2 2m dx ψ 2 ( ) 2 d x m U ⇒ = − ψ ( E ) ( ) x 2 � 2 dx 2m(U-E) α ψ α 2 = ( ); = x � 2 ⇒ ψ = + α + − α x x General Solutions : ( ) x Ae Be ψ Require finiteness of ( ) x ⇒ ψ = + α x ( ) .....x<0 (region I) x A e ψ = − α x ( ) .....x>L (regi on III ) x Ae Again, coefficients A & B come from matching conditions at the edge of the walls (x =0, L) ψ ≠ But note th at wave fn at ( ) at (x =0, L) 0 ! ! (why?) x ψ ( ) d x ψ Further require Continuity of ( ) and x dx These lead to rather different wave funct ions Finite Potential Well: Particle can Burrow Outside Box

Finite Potential Well: Particle can Burrow Outside Box Particle can be outside the box but only for a time ∆ t ≈ h/ ∆ E ∆ E = Energy particle needs to borrow to Get outside ∆ E = U-E + KE The Cinderella act (of violating E Conservation cant last very long Particle must hurry back (cant be caught with its hand inside the cookie-jar) � 1 δ Penetration Length = = α 2m(U-E) ⇒ If U>>E Tiny penetration → ∞ ⇒ δ → If U 0 Finite Potential Well: Particle can Burrow Outside Box � 1 δ Penetration Length = = α 2m(U-E) ⇒ If U>>E Tiny penetration → ∞ ⇒ δ → If U 0 π 2 2 � 2 n = E = , 1,2,3,4... n + δ n 2 2 ( 2 ) m L When E=U then solutions blow up ⇒ < Limits to number of bound states(E ) U n When E>U, particle is not bound and can get either reflected or transmitted across the potential "b arrier"

Simple Harmonic Oscillator: Quantum and Classical Spring with Force Const k m X=0 x U(x) Unstable Stable Equilibrium: General Form : 1 − 2 U(x) =U(a)+ ( ) k x a 2 1 ⇒ = − 2 R escale ( ) ( ) U x k x a 2 c Motion of a Classical Os cillator (ideal) x a b Ball originally displaced from its equilib irium Stable Stable position, mo tion co nfined betw e en x =0 & x=A 1 1 k = ω ω = = 2 2 2 U(x)= ; . Particle of mass m within a potential U(x) kx m x Ang F req 2 2 m � ( ) dU x 1 F(x)= - = ⇒ 2 Changing A changes E E kA dx 2 � → → ( ) E can take any value & if A 0, E 0 dU x = F(x=a) = - 0, ± Max. KE at x = 0, KE= 0 at x= A dx � � F(x=b) = 0 , F(x=c)=0 ...But... look at the Cur vature: ∂ ∂ 2 2 U U > 0 (stable), < 0 (uns tabl ) e ∂ ∂ 2 2 x x

Quantum Picture: Harmonic Oscillator ψ Find the Ground state Wave Function (x) 1 ω 2 2 Find the Ground state Energy E when U(x)= 2 m x ∂ ψ � 2 2 - ( ) 1 x + ω ψ = ψ 2 2 Time Dependen t Schrodinger Eqn: ( ) ( ) m x x E x ∂ 2 2 m x 2 ψ 2 ( ) 2 1 d x m ⇒ = − ω x ψ = ψ 2 2 ( ) ( ) 0 What (x) solves this? E 2 m x 2 � 2 dx Two guesses about the simplest Wavefunction: ψ ψ → → ∞ 1. (x) should be symmetric about x 2. (x) 0 as x ψ (x) d ψ + (x) should be continuous & = continu o s u dx ψ e α − 2 α x My guess: (x) = C ; Need to find C & : 0 0 What does this wavefu nct ion & PDF l ook like? Quantum Picture: Harmonic Oscillator − α 2 2 2 x P(x) = C e 0 C 2 e α − ψ 2 x (x) = C 0 C 0 x How to Get C 0 & α ?? …Try plugging in the wave-function into the time-independent Schr. Eqn.

Time Independent Sch. Eqn & The Harmonic Oscillator ∂ ψ 2 ( ) 2 1 x m = ω − ψ 2 2 Master Equation is : [ ] ( ) m x E x ∂ 2 � 2 x 2 ψ ( ) d x − α − α ψ = 2 = − α 2 x x Since ( ) , ( 2 ) , x C e C x e 0 0 dx ψ − α 2 d ( ) x d ( 2 x ) − α 2 − α 2 − α 2 = + − α = α − α 2 2 2 x x x ( 2 ) [4 2 ] C e C x e C x e 0 0 0 2 dx dx 2 1 m − α 2 − α 2 ⇒ α − α = ω − 2 2 2 2 x x [ 4 2 ] [ ] C x e m x E C e 0 0 � 2 2 2 Match t he coeff of x and the Constant terms on LHS & RHS ω 2 1 m m ⇒ α = ω α 2 2 4 or = m � � 2 2 2 2 m E α α ⇒ & the other match gives 2 = , substituing � 2 1 ω � E= =hf !!!!...... Planck's Oscil ( la tor s ) 2 What about ? We learn about that from the Normalization cond. C 0 SHO: Normalization Condition +∞ +∞ − ω 2 m x ∫ ∫ ψ = = 2 2 � | ( ) | 1 x dx C e dx 0 0 −∞ −∞ +∞ π ∫ − 2 = ax Si nce e dx (dont memorize this) a −∞ ω m Identi fying a= and using th e identity above � 1 ω ⎡ ⎤ m 4 ⇒ = C ⎢ ⎥ π 0 � ⎣ ⎦ Hence the Complete NORMA L IZED wave function is : 1 ω − ω 2 ⎡ ⎤ m x m 4 ψ (x) = � Ground State Wavefunction e 2 ⎢ ⎥ π 0 ⎣ � ⎦ has energy E = h f Planck's Oscillators were electrons tied by the "spring" of the mutually attractive Coulomb Force

Quantum Oscillator In Pictures Quantum Mechanical Prob for particle = + > ( ) 0 for n=0 E KE U x To live outside classical turning points Is finite ! U(x) C 0 U +A -A -A +A Classically particle most likely to be at the turning point (velocity=0) Quantum Mechanically , particle most likely to be at x=x 0 for n=0 Classical & Quantum Pictures of SHO compared • Limits of classical vibration : Turning Points (do on Board) • Quantum Probability for particle outside classical turning points P(|x|>A) =16% !! – Do it on the board (see Example problems in book)

Excited States of The Quantum Oscillator ω 2 m x − ψ = � ( ) ( ) 2 ; x C H x e n n n = ( ) Hermite Polynomials H x n with H (x)=1 0 H (x)=2x 1 − 2 H (x)=4x 2 2 − 3 H ( x)=8x 1 2 x 3 − 2 n x d e 2 n x H (x )=(-1) e n n d x and 1 1 = + ω = + � ( ) ( ) E n n hf n 2 2 ∞ Again n=0,1,2,3... Qu antum # Excited States of The Quantum Oscillator Ground State Energy >0 always

Measurement Expectation: Statistics Lesson • Ensemble & probable outcome of a single measurement or the average outcome of a large # of measurements ∞ n ∑ ∫ ( ) xP x dx n x + + + i i .... n x n x n x n x < >= = = = −∞ 1 1 2 2 3 3 1 i i i x ∞ + + + ... n n n n N ∫ 1 2 3 i ( ) P x dx − ∞ For a general Fn f(x) : Sharpness of A Distr ∞ n ∑ ∫ ψ ψ * ( ) ( ) ( ) x f x x dx ( ) n f x Scatter around average i i < >= = = −∞ ( ) i 1 f x ∑ ∞ − 2 N (x ) x ∫ σ ( ) i P x dx = N −∞ σ − 2 2 = ( ) ( ) x x σ → = small Sharp distr. ∆ σ Uncertainty X = Particle in the Box, n=1, <x> & ∆ x ? π ⎛ ⎞ 2 ψ (x)= sin ⎜ x ⎟ ⎝ ⎠ L L ∞ π π ⎛ ⎞ ⎛ ⎞ 2 sin 2 ∫ <x>= ⎜ ⎟ sin ⎜ ⎟ x x x dx ⎝ ⎠ ⎝ ⎠ L L L L ∞ - π π L ⎛ ⎞ ⎛ ⎞ 2 ∫ θ 2 = sin ⎜ ⎟ , change variable = ⎜ ⎟ x x dx x ⎝ ⎠ ⎝ ⎠ L L L 0 π 2 1 ∫ ⇒ θ θ θ = − θ 2 2 <x>= sin , use sin (1 cos2 ) π 2 L 2 0 ⎡ π π ⎤ 2L ∫ ∫ ∫ ∫ ⇒ θ θ θ θ θ ⎢ ⎥ <x>= d - cos2 use ud v=uv- vdu d π 2 2 ⎣ ⎦ 0 0 ⎛ ⎞ = π 2 L L ⇒ ψ 2 <x>= ⎜ ⎟ (same result as from graphing ( )) x π 2 ⎝ 2 ⎠ 2 π L 2 2 L L ∫ = − 2 2 2 Similarly <x >= x s in ( ) x dx π 2 3 2 L 0 2 2 2 L L L ∆ > − < > = − − = 2 2 and X= <x 0.18 x L π 2 3 2 4 ∆ X= 20% of L, Particle not sharply confi ned in Box