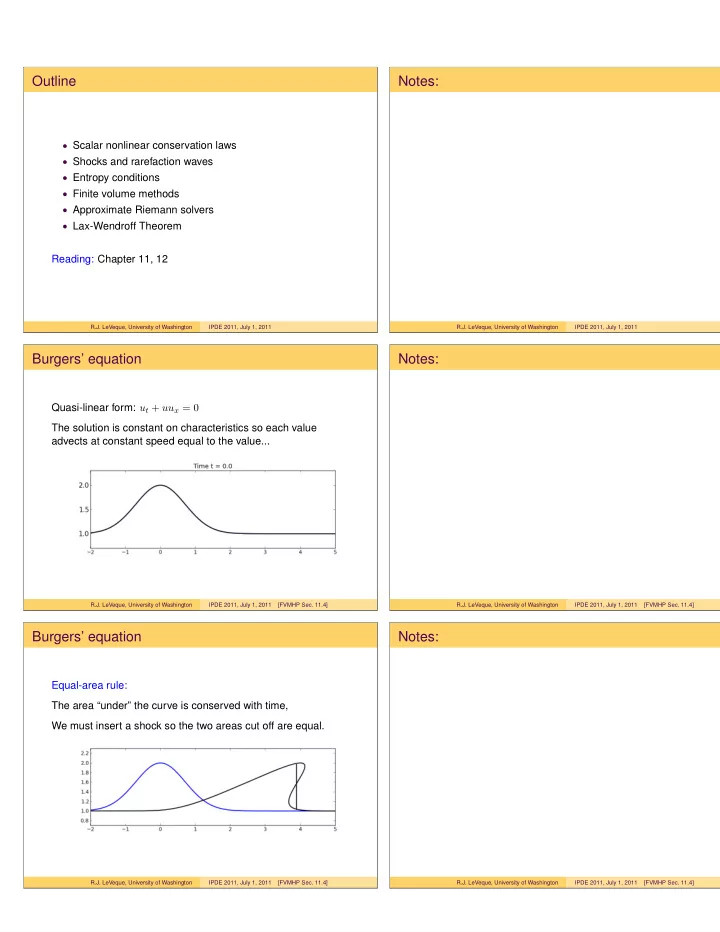
Outline Notes: Scalar nonlinear conservation laws Shocks and - PDF document

Outline Notes: • Scalar nonlinear conservation laws • Shocks and rarefaction waves • Entropy conditions • Finite volume methods • Approximate Riemann solvers • Lax-Wendroff Theorem Reading: Chapter 11, 12 R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 Burgers’ equation Notes: Quasi-linear form: u t + uu x = 0 The solution is constant on characteristics so each value advects at constant speed equal to the value... R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] Burgers’ equation Notes: Equal-area rule: The area “under” the curve is conserved with time, We must insert a shock so the two areas cut off are equal. R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4]

Riemann problem for Burgers’ equation Notes: � 1 2 u 2 � u t + x = 0 , u t + uu x = 0 . f ( u ) = 1 2 u 2 , f ′ ( u ) = u. Consider Riemann problem with states u ℓ and u r . For any u ℓ , u r , there is a weak solution consisting of this discontinuity propagating at speed given by the Rankine-Hugoniot jump condition: 1 r − 1 2 u 2 2 u 2 = 1 ℓ s = 2( u ℓ + u r ) . u r − u ℓ Note: Shock speed is average of characteristic speed on each side. This might not be the physically correct weak solution! R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] Burgers’ equation Notes: The solution is constant on characteristics so each value advects at constant speed equal to the value... R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.4] Weak solutions to Burgers’ equation Notes: � 1 2 u 2 � u t + x = 0 , u ℓ = 1 , u r = 2 Rankine-Hugoniot speed: 1 Characteristic speed: u 2 ( u ℓ + u r ) . “Physically correct” rarefaction wave solution: R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ]

Weak solutions to Burgers’ equation Notes: � 1 2 u 2 � u t + x = 0 , u ℓ = 1 , u r = 2 Rankine-Hugoniot speed: 1 Characteristic speed: u 2 ( u ℓ + u r ) . Entropy violating weak solution: R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] Weak solutions to Burgers’ equation Notes: � 1 2 u 2 � u t + x = 0 , u ℓ = 1 , u r = 2 Rankine-Hugoniot speed: 1 Characteristic speed: u 2 ( u ℓ + u r ) . Another Entropy violating weak solution: R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] Vanishing viscosity solution Notes: We want q ( x, t ) to be the limit as ǫ → 0 of solution to q t + f ( q ) x = ǫq xx . This selects a unique weak solution: • Shock if f ′ ( q l ) > f ′ ( q r ) , • Rarefaction if f ′ ( q l ) < f ′ ( q r ) . Lax Entropy Condition: A discontinuity propagating with speed s in the solution of a convex scalar conservation law is admissible only if f ′ ( q ℓ ) > s > f ′ ( q r ) , where s = ( f ( q r ) − f ( q ℓ )) / ( q r − q ℓ ) . Note: This means characteristics must approach shock from both sides as t advances, not move away from shock! R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ]

Riemann problem for scalar nonlinear problem Notes: q t + f ( q ) x = 0 with data � q l if x < 0 q ( x, 0) = q r if x ≥ 0 Piecewise constant with a single jump discontinuity. For Burgers’ or traffic flow with quadratic flux, the Riemann solution consists of: • Shock wave if f ′ ( q l ) > f ′ ( q r ) , • Rarefaction wave if f ′ ( q l ) < f ′ ( q r ) . Five possible cases: R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.1] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.1] Transonic rarefactions Notes: Sonic point: u s = 0 for Burgers’ since f ′ (0) = 0 . Consider Riemann problem data u ℓ = − 0 . 5 < 0 < u r = 1 . 5 . In this case wave should spread in both directions: R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] Transonic rarefactions Notes: Entropy-violating approximate Riemann solution: s = 1 2( u ℓ + u r ) = 0 . 5 . Wave goes only to right, no update to cell average on left. R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ]

Transonic rarefactions Notes: If u ℓ = − u r then Rankine-Hugoniot speed is 0: Similar solution will be observed with Godunov’s method if entropy-violating approximate Riemann solver used. R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 11.13 ] Entropy-violating numerical solutions Notes: Riemann problem for Burgers’ equation at t = 1 with u ℓ = − 1 and u r = 2 : Godunov with no entropy fix Godunov with entropy fix 2.5 2.5 2 2 1.5 1.5 1 1 0.5 0.5 0 0 −0.5 −0.5 −1 −1 −1.5 −1.5 −3 −2 −1 0 1 2 3 −3 −2 −1 0 1 2 3 High−resolution with no entropy fix High−resolution with entropy fix 2.5 2.5 2 2 1.5 1.5 1 1 0.5 0.5 0 0 −0.5 −0.5 −1 −1 −1.5 −1.5 −3 −2 −1 0 1 2 3 −3 −2 −1 0 1 2 3 R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.3] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.3] Approximate Riemann solvers Notes: For nonlinear problems, computing the exact solution to each Riemann problem may not be possible, or too expensive. Often the nonlinear problem q t + f ( q ) x = 0 is approximated by q t + A i − 1 / 2 q x = 0 , q ℓ = Q i − 1 , q r = Q i for some choice of A i − 1 / 2 ≈ f ′ ( q ) based on data Q i − 1 , Q i . p α p i − 1 / 2 r p Solve linear system for α i − 1 / 2 : Q i − Q i − 1 = � i − 1 / 2 . Waves W p i − 1 / 2 = α p i − 1 / 2 r p i − 1 / 2 propagate with speeds s p i − 1 / 2 , r p i − 1 / 2 are eigenvectors of A i − 1 / 2 , s p i − 1 / 2 are eigenvalues of A i − 1 / 2 . R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 15.3.2 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 15.3.2 ]

Approximate Riemann solvers Notes: q t + ˆ A i − 1 / 2 q x = 0 , q ℓ = Q i − 1 , q r = Q i Often ˆ A i − 1 / 2 = f ′ ( Q i − 1 / 2 ) for some choice of Q i − 1 / 2 . In general ˆ A i − 1 / 2 = ˆ A ( q ℓ , q r ) . Roe conditions for consistency and conservation: • ˆ A ( q ℓ , q r ) → f ′ ( q ∗ ) q ℓ , q r → q ∗ , as • ˆ A diagonalizable with real eigenvalues, • For conservation in wave-propagation form, ˆ A i − 1 / 2 ( Q i − Q i − 1 ) = f ( Q i ) − f ( Q i − 1 ) . R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 15.3.2 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 15.3.2 ] Approximate Riemann solvers Notes: For a scalar problem, we can easily satisfy the Roe condition ˆ A i − 1 / 2 ( Q i − Q i − 1 ) = f ( Q i ) − f ( Q i − 1 ) . by choosing A i − 1 / 2 = f ( Q i ) − f ( Q i − 1 ) ˆ . Q i − Q i − 1 i − 1 / 2 = ˆ Then r 1 i − 1 / 2 = 1 and s 1 A i − 1 / 2 (scalar!). Note: This is the Rankine-Hugoniot shock speed. = ⇒ shock waves are correct, rarefactions replaced by entropy-violating shocks. R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.2 ] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.2 ] Approximate Riemann solver Notes: i − ∆ t Q n +1 = Q n A + ∆ Q i − 1 / 2 + A − ∆ Q i +1 / 2 � � . i ∆ x For scalar advection m = 1 , only one wave. W i − 1 / 2 = ∆ Q i − 1 / 2 = Q i − Q i − 1 and s i − 1 / 2 = u , A − ∆ Q i − 1 / 2 = s − i − 1 / 2 W i − 1 / 2 , A + ∆ Q i − 1 / 2 = s + i − 1 / 2 W i − 1 / 2 . For scalar nonlinear: Use same formulas with W i − 1 / 2 = ∆ Q i − 1 / 2 and s i − 1 / 2 = ∆ F i − 1 / 2 / ∆ Q i − 1 / 2 . Need to modify these by an entropy fix in the trans-sonic rarefaction case. R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.3] R.J. LeVeque, University of Washington IPDE 2011, July 1, 2011 [FVMHP Sec. 12.3]