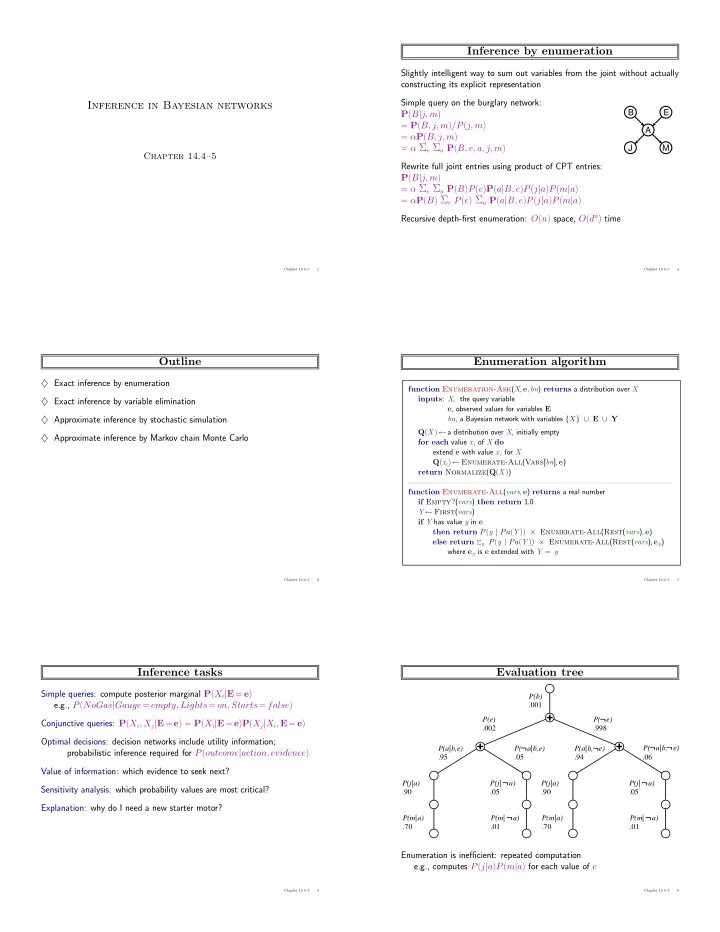
Inference by enumeration Slightly intelligent way to sum out - PDF document

Inference by enumeration Slightly intelligent way to sum out variables from the joint without actually constructing its explicit representation Simple query on the burglary network: Inference in Bayesian networks B E P ( B | j, m ) = P ( B, j, m ) /P ( j, m ) A = α P ( B, j, m ) J M = α Σ e Σ a P ( B, e, a, j, m ) Chapter 14.4–5 Rewrite full joint entries using product of CPT entries: P ( B | j, m ) = α Σ e Σ a P ( B ) P ( e ) P ( a | B, e ) P ( j | a ) P ( m | a ) = α P ( B ) Σ e P ( e ) Σ a P ( a | B, e ) P ( j | a ) P ( m | a ) Recursive depth-first enumeration: O ( n ) space, O ( d n ) time Chapter 14.4–5 1 Chapter 14.4–5 4 Outline Enumeration algorithm ♦ Exact inference by enumeration function Enumeration-Ask ( X , e , bn ) returns a distribution over X inputs : X , the query variable ♦ Exact inference by variable elimination e , observed values for variables E ♦ Approximate inference by stochastic simulation bn , a Bayesian network with variables { X } ∪ E ∪ Y Q ( X ) ← a distribution over X , initially empty ♦ Approximate inference by Markov chain Monte Carlo for each value x i of X do extend e with value x i for X Q ( x i ) ← Enumerate-All ( Vars [ bn ], e ) return Normalize ( Q ( X ) ) function Enumerate-All ( vars , e ) returns a real number if Empty? ( vars ) then return 1.0 Y ← First ( vars ) if Y has value y in e then return P ( y | Pa ( Y )) × Enumerate-All ( Rest ( vars ), e ) else return � y P ( y | Pa ( Y )) × Enumerate-All ( Rest ( vars ), e y ) where e y is e extended with Y = y Chapter 14.4–5 2 Chapter 14.4–5 5 Inference tasks Evaluation tree Simple queries: compute posterior marginal P ( X i | E = e ) P(b) .001 e.g., P ( NoGas | Gauge = empty, Lights = on, Starts = false ) P(e) P( e) Conjunctive queries: P ( X i , X j | E = e ) = P ( X i | E = e ) P ( X j | X i , E = e ) .002 .998 Optimal decisions: decision networks include utility information; P( a|b, e) P(a|b,e) P( a|b,e) P(a|b, e) probabilistic inference required for P ( outcome | action, evidence ) .95 .05 .94 .06 Value of information: which evidence to seek next? P(j|a) P(j| a) P(j|a) P(j| a) Sensitivity analysis: which probability values are most critical? .90 .05 .90 .05 Explanation: why do I need a new starter motor? P(m|a) P(m| a) P(m|a) P(m| a) .70 .01 .70 .01 Enumeration is inefficient: repeated computation e.g., computes P ( j | a ) P ( m | a ) for each value of e Chapter 14.4–5 3 Chapter 14.4–5 6

Inference by variable elimination Irrelevant variables Variable elimination: carry out summations right-to-left, Consider the query P ( JohnCalls | Burglary = true ) B E storing intermediate results (factors) to avoid recomputation A P ( B | j, m ) P ( J | b ) = αP ( b ) � e P ( e ) � a P ( a | b, e ) P ( J | a ) � m P ( m | a ) Σ e P ( e ) Σ a P ( a | B, e ) = α P ( B ) P ( j | a ) P ( m | a ) J M Sum over m is identically 1; M is irrelevant to the query � �� � � �� � � �� � � �� � � �� � B E A J M = α P ( B ) Σ e P ( e ) Σ a P ( a | B, e ) P ( j | a ) f M ( a ) = α P ( B ) Σ e P ( e ) Σ a P ( a | B, e ) f J ( a ) f M ( a ) Thm 1: Y is irrelevant unless Y ∈ Ancestors ( { X } ∪ E ) = α P ( B ) Σ e P ( e ) Σ a f A ( a, b, e ) f J ( a ) f M ( a ) = α P ( B ) Σ e P ( e ) f ¯ AJM ( b, e ) (sum out A ) Here, X = JohnCalls , E = { Burglary } , and = α P ( B ) f ¯ AJM ( b ) (sum out E ) Ancestors ( { X } ∪ E ) = { Alarm, Earthquake } E ¯ = αf B ( b ) × f ¯ AJM ( b ) so MaryCalls is irrelevant E ¯ (Compare this to backward chaining from the query in Horn clause KBs) Chapter 14.4–5 7 Chapter 14.4–5 10 Variable elimination: Basic operations Irrelevant variables contd. Summing out a variable from a product of factors: Defn: moral graph of Bayes net: marry all parents and drop arrows move any constant factors outside the summation Defn: A is m-separated from B by C iff separated by C in the moral graph add up submatrices in pointwise product of remaining factors Thm 2: Y is irrelevant if m-separated from X by E Σ x f 1 × · · · × f k = f 1 × · · · × f i Σ x f i +1 × · · · × f k = f 1 × · · · × f i × f ¯ B E X assuming f 1 , . . . , f i do not depend on X A For P ( JohnCalls | Alarm = true ) , both Burglary and Earthquake are irrelevant Pointwise product of factors f 1 and f 2 : J M f 1 ( x 1 , . . . , x j , y 1 , . . . , y k ) × f 2 ( y 1 , . . . , y k , z 1 , . . . , z l ) = f ( x 1 , . . . , x j , y 1 , . . . , y k , z 1 , . . . , z l ) E.g., f 1 ( a, b ) × f 2 ( b, c ) = f ( a, b, c ) Chapter 14.4–5 8 Chapter 14.4–5 11 Variable elimination algorithm Complexity of exact inference Singly connected networks (or polytrees): function Elimination-Ask ( X , e , bn ) returns a distribution over X – any two nodes are connected by at most one (undirected) path inputs : X , the query variable – time and space cost of variable elimination are O ( d k n ) e , evidence specified as an event bn , a belief network specifying joint distribution P ( X 1 , . . . , X n ) Multiply connected networks: factors ← [ ] ; vars ← Reverse ( Vars [ bn ]) – can reduce 3SAT to exact inference ⇒ NP-hard for each var in vars do – equivalent to counting 3SAT models ⇒ #P-complete factors ← [ Make-Factor ( var , e ) | factors ] if var is a hidden variable then factors ← Sum-Out ( var , factors ) 0.5 0.5 0.5 0.5 return Normalize ( Pointwise-Product ( factors )) A B C D L L 1. A v B v C 2. C v D v A 1 2 3 L 3. B v C v D L AND Chapter 14.4–5 9 Chapter 14.4–5 12

Inference by stochastic simulation Example P(C) Basic idea: .50 1) Draw N samples from a sampling distribution S 0.5 2) Compute an approximate posterior probability ˆ P Cloudy 3) Show this converges to the true probability P Coin Outline: C P(S|C) C P(R|C) – Sampling from an empty network Rain T .10 Sprinkler T .80 – Rejection sampling: reject samples disagreeing with evidence F .50 F .20 – Likelihood weighting: use evidence to weight samples Wet – Markov chain Monte Carlo (MCMC): sample from a stochastic process Grass whose stationary distribution is the true posterior S R P(W|S,R) T T .99 T F .90 F T .90 F F .01 Chapter 14.4–5 13 Chapter 14.4–5 16 Sampling from an empty network Example P(C) function Prior-Sample ( bn ) returns an event sampled from bn .50 inputs : bn , a belief network specifying joint distribution P ( X 1 , . . . , X n ) x ← an event with n elements Cloudy for i = 1 to n do x i ← a random sample from P ( X i | parents ( X i )) C P(S|C) C P(R|C) given the values of Parents ( X i ) in x Rain T .10 Sprinkler T .80 return x F .50 F .20 Wet Grass S R P(W|S,R) T T .99 T F .90 F T .90 F F .01 Chapter 14.4–5 14 Chapter 14.4–5 17 Example Example P(C) P(C) .50 .50 Cloudy Cloudy C P(S|C) C P(R|C) C P(S|C) C P(R|C) Rain Rain T .10 Sprinkler T .80 T .10 Sprinkler T .80 F .50 F .20 F .50 F .20 Wet Wet Grass Grass S R P(W|S,R) S R P(W|S,R) T T .99 T T .99 T F .90 T F .90 F T .90 F T .90 F F .01 F F .01 Chapter 14.4–5 15 Chapter 14.4–5 18

Example Sampling from an empty network contd. P(C) Probability that PriorSample generates a particular event .50 S PS ( x 1 . . . x n ) = Π n i = 1 P ( x i | parents ( X i )) = P ( x 1 . . . x n ) i.e., the true prior probability Cloudy E.g., S PS ( t, f, t, t ) = 0 . 5 × 0 . 9 × 0 . 8 × 0 . 9 = 0 . 324 = P ( t, f, t, t ) C P(S|C) C P(R|C) Let N PS ( x 1 . . . x n ) be the number of samples generated for event x 1 , . . . , x n Rain T .10 Sprinkler T .80 Then we have F .50 F .20 ˆ Wet lim P ( x 1 , . . . , x n ) = N →∞ N PS ( x 1 , . . . , x n ) /N lim Grass N →∞ = S PS ( x 1 , . . . , x n ) S R P(W|S,R) = P ( x 1 . . . x n ) T T .99 That is, estimates derived from PriorSample are consistent T F .90 F T .90 Shorthand: ˆ P ( x 1 , . . . , x n ) ≈ P ( x 1 . . . x n ) F F .01 Chapter 14.4–5 19 Chapter 14.4–5 22 Example Rejection sampling P(C) ˆ P ( X | e ) estimated from samples agreeing with e .50 function Rejection-Sampling ( X , e , bn , N ) returns an estimate of P ( X | e ) Cloudy local variables : N , a vector of counts over X , initially zero for j = 1 to N do C P(S|C) C P(R|C) x ← Prior-Sample ( bn ) Rain T .10 Sprinkler T .80 if x is consistent with e then N [ x ] ← N [ x ]+1 where x is the value of X in x F .50 F .20 return Normalize ( N [ X ]) Wet Grass E.g., estimate P ( Rain | Sprinkler = true ) using 100 samples S R P(W|S,R) 27 samples have Sprinkler = true T T .99 Of these, 8 have Rain = true and 19 have Rain = false . T F .90 ˆ P ( Rain | Sprinkler = true ) = Normalize ( � 8 , 19 � ) = � 0 . 296 , 0 . 704 � F T .90 F F .01 Similar to a basic real-world empirical estimation procedure Chapter 14.4–5 20 Chapter 14.4–5 23 Example Analysis of rejection sampling P(C) ˆ P ( X | e ) = α N PS ( X, e ) (algorithm defn.) .50 = N PS ( X, e ) /N PS ( e ) (normalized by N PS ( e ) ) ≈ P ( X, e ) /P ( e ) (property of PriorSample ) Cloudy = P ( X | e ) (defn. of conditional probability) C P(S|C) C P(R|C) Hence rejection sampling returns consistent posterior estimates Rain T .10 Sprinkler T .80 Problem: hopelessly expensive if P ( e ) is small F .50 F .20 P ( e ) drops off exponentially with number of evidence variables! Wet Grass S R P(W|S,R) T T .99 T F .90 F T .90 F F .01 Chapter 14.4–5 21 Chapter 14.4–5 24