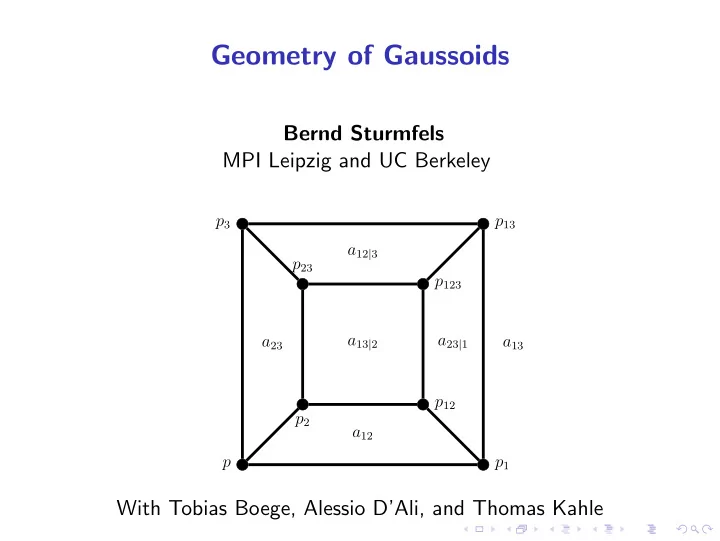
Geometry of Gaussoids Bernd Sturmfels MPI Leipzig and UC Berkeley p - PowerPoint PPT Presentation

Geometry of Gaussoids Bernd Sturmfels MPI Leipzig and UC Berkeley p 3 p 13 a 12 | 3 p 23 p 123 a 13 | 2 a 23 | 1 a 23 a 13 p 12 p 2 a 12 p p 1 With Tobias Boege, Alessio D’Ali, and Thomas Kahle

12 Matroids 14 24 13 23 34 A matroid is a combinatorial structure that encodes independence in linear algebra and geometry. The basis axioms reflect the ideal of homogeneous relations among all minors of a rectangular matrix � 1 � 1 � � 0 0 − p 23 − p 24 � � = 0 1 0 1 p 13 p 14 � � A matroid is an assignment of 0 or ⋆ to these minors so that the quadratic Pl¨ ucker relations have a chance of vanishing: p 12 p 34 − p 13 p 24 + p 14 p 23 = 0 . We also like oriented matroids , positroids and valuated matroids .

Gaussoids A gaussoid is a combinatorial structure that encodes independence in probability and statistics. The gaussoid axioms reflect the ideal of homogeneous relations among the principal and almost-principal minors of a symmetric matrix � 1 � 1 � � 0 0 p 1 a 12 � � = 0 1 � � 0 1 a 12 p 2 A gaussoid is an assignment of 0 or ⋆ to these minors so that the quadratic Pl¨ ucker relations have a chance of vanishing: p · p 12 − p 1 · p 2 + a 2 12 = 0 . Ditto: oriented gaussoids , positive gaussoids , valuated gaussoids . The gaussoid axioms were introduced in [R. Lnˇ eniˇ cka and F. Mat´ uˇ s: On Gaussian conditional independence structures, Kybernetika (2007)]

Principal and almost-principal minors A symmetric n × n -matrix Σ has 2 n principal minors p I one for each subset I of [ n ] = { 1 , 2 , . . . , n } . The matrix Σ has 2 n − 2 � n � almost-principal minors a ij | K . 2 This is the subdeterminant of Σ with row indices { i } ∪ K and column indices { j } ∪ K , where i , j ∈ [ n ] and K ⊆ [ n ] \{ i , j } . Principal minors are in bijection with the vertices of the n -cube. Almost-principal minors are in bijection with the 2-faces of the n -cube. p 3 p 13 a 12 | 3 p 23   p 1 a 12 a 13 p 123 Σ = a 12 p 2 a 23   a 13 a 23 p 3 a 23 a 13 | 2 a 23 | 1 a 13 p 12 p 2 a 12 p p 1

Why Gauss? If Σ is positive definite then it is the covariance matrix of a Gaussian distribution on R n . In statistics: p I > 0 for all I ⊆ [ n ]. Study n random variables X 1 , X 2 , . . . , X n , with the aim of learning how they are related. (Yes, data science) Almost-principal minors a ij | K measure partial correlations. We have a ij | K = 0 if and only if X i and X j are conditionally independent given X K . The inequalities a ij | K > 0 and a ij | K < 0 indicate whether conditional correlation is positive or negative.

Ideals, Varieties, ... Write J n for the homogeneous prime ideal of relations among the principal and almost-principal minors of a symmetric n × n -matrix. It lives in a polynomial ring R [ p , a ] with N = 2 n + 2 n − 2 � n � 2 unknowns, and defines an irreducible subvariety of P N − 1 . Proposition The projective variety V ( J n ) is a coordinate projection of the Lagrangian Grassmannian. They share dimension and degree: � n +1 � dim ( V ( J n )) = 2 � n +1 � ! 2 degree ( V ( J n )) = 1 n · 3 n − 1 · 5 n − 2 · · · (2 n − 1) 1 . The elimination ideal J n ∩ R [ p ] was studied by Holtz-St and Oeding. They found hyperdeterminantal relations of degree 4.

3-cube The ideal J 3 is generated by 21 quadrics. There are 9 quadrics associated with the facets of the 3-cube: a 2  (2 , 0 , 0) 23 + pp 23 − p 2 p 3  (0 , 0 , 0) 2 a 23 a 23 | 1 + pp 123 + p 1 p 23 − p 2 p 13 − p 12 p 3 S 200   a 2 ( − 2 , 0 , 0) 23 | 1 + p 1 p 123 − p 12 p 13 .... and two other such weight components There are 12 trinomials associated with the edge of the 3-cube:   (1 , 1 , 0) a 13 a 23 + a 12 | 3 p − a 12 p 3 (1 , − 1 , 0) a 13 | 2 a 23 + a 12 | 3 p 2 − a 12 p 23   S 110   ( − 1 , 1 , 0) a 13 a 23 | 1 + a 12 | 3 p 1 − a 12 p 13   ( − 1 , − 1 , 0) a 13 | 2 a 23 | 1 + a 12 | 3 p 12 − a 12 p 123 .... and two other such weight components The variety V ( J 3 ) is the Lagrangian Grassmannian in P 13 , which has dimension 6 and degree 16. It is arithmetically Gorenstein. Intersections with subspaces P 8 are canonical curves of genus 9 .

3-cube Of most interest are the 12 edge trinomials: p 1 a 23 − pa 23 | 1 − a 12 a 13 p 2 a 13 − pa 13 | 2 − a 12 a 23 p 3 a 12 − pa 12 | 3 − a 23 a 13 p 12 a 13 − p 1 a 13 | 2 − a 12 a 23 | 1 p 12 a 23 − p 2 a 23 | 1 − a 12 a 13 | 2 p 13 a 12 − p 1 a 12 | 3 − a 13 a 23 | 1 p 13 a 23 − p 3 a 23 | 1 − a 13 a 12 | 3 p 23 a 12 − p 2 a 12 | 3 − a 23 a 13 | 2 p 23 a 13 − p 3 a 13 | 2 − a 23 a 12 | 3 p 123 a 12 − p 12 a 12 | 3 − a 23 | 1 a 13 | 2 p 123 a 13 − p 13 a 13 | 2 − a 23 | 1 a 12 | 3 p 123 a 23 − p 23 a 23 | 1 − a 12 | 3 a 13 | 2 p 3 p 13 a 12 | 3 p 23 p 123 a 23 a 13 | 2 a 23 | 1 a 13 p 12 p 2 a 12 p p 1

Gaussoid Axioms 2 n − 2 symbols a ij | K . Following Lnˇ � n � Let A be the set of eniˇ cka 2 and Mat´ uˇ s, a subset G of A is a gaussoid on [ n ] if it satisfies: 1. { a ij | L , a ik | jL } ⊂ G implies { a ik | L , a ij | kL } ⊂ G , 2. { a ij | kL , a ik | jL } ⊂ G implies { a ij | L , a ik | L } ⊂ G , 3. { a ij | L , a ik | L } ⊂ G implies { a ij | kL , a ik | jL } ⊂ G , � � 4. { a ij | L , a ij | kL } ⊂ G implies a ik | L ∈ G or a jk | L ∈ G . These axioms are known as 1. semigraphoid , 2. intersection , 3. converse to intersection , 4. weak transitivity .

Gaussoid Axioms 2 n − 2 symbols a ij | K . Following Lnˇ � n � Let A be the set of eniˇ cka 2 and Mat´ uˇ s, a subset G of A is a gaussoid on [ n ] if it satisfies: 1. { a ij | L , a ik | jL } ⊂ G implies { a ik | L , a ij | kL } ⊂ G , 2. { a ij | kL , a ik | jL } ⊂ G implies { a ij | L , a ik | L } ⊂ G , 3. { a ij | L , a ik | L } ⊂ G implies { a ij | kL , a ik | jL } ⊂ G , � � 4. { a ij | L , a ij | kL } ⊂ G implies a ik | L ∈ G or a jk | L ∈ G . These axioms are known as 1. semigraphoid , 2. intersection , 3. converse to intersection , 4. weak transitivity . Theorem The following are equivalent for a set G of 2 -faces of the n-cube: (a) G is a gaussoid, i.e. the four axioms above are satisfied for G . (b) G is compatible with the quadratic edge trinomials in J n .

Duality and Minors Let G be any gaussoid on [ n ]. The dual of G is G ∗ = � � a ij | L : a ij | K ∈ G and L = [ n ] \ ( { i , j } ∪ K ) . Fix an element u ∈ [ n ]. The marginalization equals � � G\ u = a ij | K ∈ G : u �∈ { i , j } ∪ K . The conditioning equals � � G / u = a ij | K \{ u } : a ij | K ∈ G and u ∈ K . Think of operations on sets of 2-faces of the n -cube. Proposition If G is a gaussoid on [ n ] , and u ∈ [ n ] , then G ∗ , G\ u and G / u are gaussoids on [ n ] \{ u } . The following duality relation holds: � ∗ = G ∗ / u � ∗ = G ∗ \ u . � � G\ u and G / u If G is realizable (with Σ positive definite) then so are G ∗ , G\ u , G / u.

A Pinch of Representation Theory Fix the Lie group G = ( SL 2 ( C )) n . Write V i ≃ C 2 for the defining representation of the i -th factor. The irreducible G -modules are n � S d 1 d 2 ··· d n = Sym d i ( V i ) , i =1 Proposition G acts on the space W pr spanned by the principal minors and the spaces W ij ap spanned by almost-principal minors. As G-modules, W pr ≃ ⊗ n W ij i =1 V i and ap ≃ ⊗ k ∈ [ n ] \{ i , j } V k for 1 ≤ i < j ≤ n. This defines the G -action and Z n -grading on our polynomial ring C [ p , a ]. i , j W ij The formal character of C [ p , a ] 1 = W pr ⊕ � ap is the sum of weights: � n i =1 ( x i + x − 1 k ∈ [ n ] \{ i , j } ( x k + x − 1 ) + � � k ) i 1 ≤ i < j ≤ n

Commutative Algebra The number of linearly independent quadrics in the ideal J n equals � n ⌊ n 2 ⌋ n − 3 � n � � n � � � � 3 n − 2 3 k ( n − k )( n − k − 1) k 3 n − 2 k + 2 + 2 2 k 2 k k =0 k =2 Derived via the lowering and raising operators in the Lie algebra g . Conjecture These quadrics generate J n . Proposition The number of face trinomials and edge trinomials equals � n � � n � 2 n − 2 + 12 · 2 n − 3 = 2 n − 3 n ( n − 1)(2 n − 3) . 2 3 These trinomials generate the image of J n in C [ p , a ± ] .

4-cube p 3 p 13 a 12 | 3 p 23 p 123 a 13 | 2 a 23 | 1 a 23 a 13 p 12 p 2 a 12 p p 1 There are 16 principal and 24 almost principal minors. They span C [ p , a ] 1 = S 1111 ⊕ S 1100 ⊕ S 1010 ⊕ S 1001 ⊕ S 0110 ⊕ S 0101 ⊕ S 0011 . The space of quadrics has dimension 820. As G -module, C [ a , p ] 2 ≃ S 2222 ⊕ S 2211 ⊕ S 2121 ⊕ S 2112 ⊕ S 1221 ⊕ S 1212 ⊕ S 1122 ⊕ 2 S 2200 ⊕ 2 S 2020 ⊕ 2 S 2002 ⊕ 2 S 0220 ⊕ 2 S 0202 ⊕ 2 S 0022 ⊕ 2 S 2110 ⊕ 2 S 2101 ⊕ 2 S 2011 ⊕ 2 S 1210 ⊕ 2 S 1201 ⊕ 2 S 0211 ⊕ 2 S 1120 ⊕ 2 S 1021 ⊕ 2 S 0121 ⊕ 2 S 1102 ⊕ 2 S 1012 ⊕ 2 S 0112 ⊕ 3 S 1111 ⊕ 3 S 1100 ⊕ 3 S 1010 ⊕ 3 S 1001 ⊕ 3 S 0110 ⊕ 3 S 0101 ⊕ 3 S 0011 ⊕ 7 S 0000 . The 226-dimensional submodule ( J 4 ) 2 of quadrics in our ideal equals S 2200 ⊕ S 2020 ⊕ S 2002 ⊕ S 0220 ⊕ S 0202 ⊕ S 0022 ⊕ S 2110 ⊕ S 2101 ⊕ S 2011 ⊕ S 1210 ⊕ S 1201 ⊕ S 0211 ⊕ S 1120 ⊕ S 1021 ⊕ S 0121 ⊕ S 1102 ⊕ S 1012 ⊕ S 0112 ⊕ S 1100 ⊕ S 1010 ⊕ S 1001 ⊕ S 0110 ⊕ S 0101 ⊕ S 0011 ⊕ 4 S 0000 . Of these, 120 are trinomials: 96 edge trinomials and 24 face trinomials.