Definition of impulse response model g ( n ) : { ( n ) } Time - PowerPoint PPT Presentation

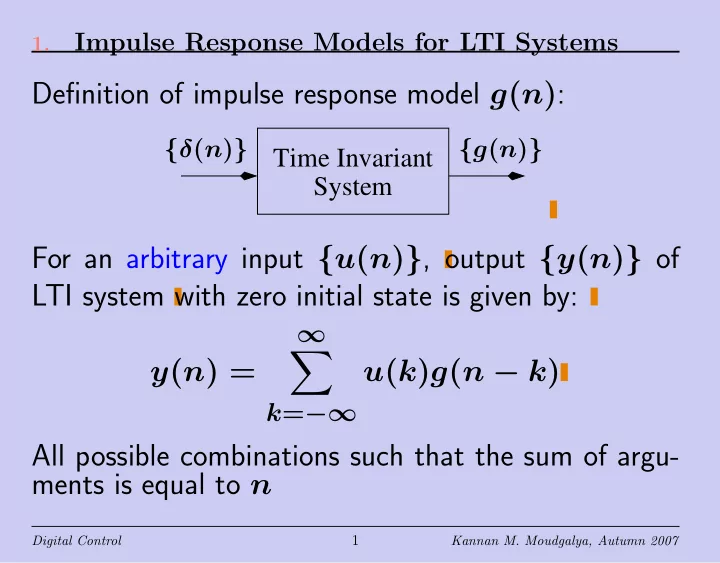
Impulse Response Models for LTI Systems 1. Definition of impulse response model g ( n ) : { δ ( n ) } Time Invariant { g ( n ) } System For an arbitrary input { u ( n ) } , output { y ( n ) } of LTI system with zero initial state is given by: ∞ � y ( n ) = u ( k ) g ( n − k ) k = −∞ All possible combinations such that the sum of argu- ments is equal to n 1 Digital Control Kannan M. Moudgalya, Autumn 2007

Importance of Impulse Response Models 2. • Impulse response has all information about LTI sys- tem • Given impulse response, can determine output due to any arbitrary input 2 Digital Control Kannan M. Moudgalya, Autumn 2007

Step Response, Relation with Impulse Response 3. The unit step response of an LTI system at zero ini- tial state { s ( n ) } is the output when { u ( n ) } = { 1( n ) } : ∞ � s ( n ) = 1( k ) g ( n − k ) k = −∞ Apply the meaning of 1( k ) : ∞ � = g ( n − k ) k =0 • This shows that the step response is the sum of impulse response. 3 Digital Control Kannan M. Moudgalya, Autumn 2007

Relation between Step and Impulse Responses 4. • We can also get impulse response from step re- sponse. δ ( n ) = 1( n ) − 1( n − 1) Using linearity and time invariance properties, g ( n ) = s ( n ) − s ( n − 1) 4 Digital Control Kannan M. Moudgalya, Autumn 2007

Causality of LTI Systems 5. • If output depends only on past inputs, called causal • If output depends on future inputs, not causal • For LTI causal systems, g ( n ) = 0 for n < 0 – Initial state is zero – No input until n = 0 - impulse input – So, impulse response can begin only from n = 0 • Signal { u ( n ) } is causal if u ( k ) = 0 for k < 0 5 Digital Control Kannan M. Moudgalya, Autumn 2007

Output of Causal Systems to Causal Signals 6. • Impulse response g ( n ) , input u ( n ) are causal: ∞ � y ( n ) = u ( k ) g ( n − k ) k = −∞ ∞ � = u ( k ) g ( n − k ) ( u ( k ) = 0 ∀ k < 0) k =0 n � = u ( k ) g ( n − k ) ( g ( k ) = 0 ∀ k < 0) k =0 6 Digital Control Kannan M. Moudgalya, Autumn 2007

Convolution Theorems 7. Convolution is Commutative: u ( n ) ∗ g ( n ) = g ( n ) ∗ u ( n ) Convolution is Associative: u ( n ) ∗ ( g 1 ( n ) ∗ g 2 ( n )) = ( u ( n ) ∗ g 1 ( n )) ∗ g 2 ( n ) Convolution Distributes over Addition: u ( n ) ∗ ( g 1 ( n ) + g 2 ( n )) = u ( n ) ∗ g 1 ( n ) + u ( n ) g 1 ( n ) u ( n ) y 2 ( n ) + u ( n ) y 1 ( n ) g 1 ( n ) + g 2 ( n ) g 2 ( n ) 7 Digital Control Kannan M. Moudgalya, Autumn 2007

External (BIBO) Stability of LTI Systems 8. If every Bounded Input produces Bounded Output, • system is externally stable • equivalently, system is BIBO stable ∞ � | g ( n ) | < ∞ ⇔ BIBO Stability n = −∞ • Don’t care about what unbounded input does... 8 Digital Control Kannan M. Moudgalya, Autumn 2007

Recall convolution example 9. ∞ � { y ( n ) } = u ( k ) { g ( n − k ) } k = −∞ { g ( n ) } = { 1 , 2 , 3 } , { u ( n ) } = { 4 , 5 , 6 } g , u start at n = 0 . They are zero for n < 0 . y (0) = u (0) g (0) = 4 y (1) = u (0) g (1) + u (1) g (0) = 13 y (2) = u (0) g (2) + u (1) g (1) + u (2) g (0) = 28 y (3) = u (1) g (2) + u (2) g (1) = 27 y (4) = u (2) g (2) = 18 All other terms that don’t appear above are zero. 9 Digital Control Kannan M. Moudgalya, Autumn 2007

Polynomial Calculation ≡ Convolution 10. Also carryout multiplication: ( u (0)+ u (1) z − 1 + u (2) z − 2 ) × ( g (0)+ g (1) z − 1 + g (2) z − 2 ) = u (0) g (0) + ( u (0) g (1) + u (1) g (0)) z − 1 + ( u (0) g (2) + u (1) g (1) + u (2) g (0)) z − 2 + ( u (1) g (2) + u (2) g (1)) z − 3 + • z a position marker - coeff. of z − i at i th instant • u (0)+ u (1) z − 1 + u (2) z − 2 - a way of represent- ing a sequence with three terms: { u (0) , u (1) , u (2) } • Even if large no. of terms, can get compact form 10 Digital Control Kannan M. Moudgalya, Autumn 2007

Definition of Z-transform 11. Z-transform of a sequence { u ( n ) } , denoted by U ( z ) , is defined as: ∞ u ( n ) z − n � U ( z ) = n = −∞ where z is such that there is absolute convergence. That is, z should be chosen so as to satisfy ∞ | u ( n ) z − n | < ∞ � n = −∞ 11 Digital Control Kannan M. Moudgalya, Autumn 2007

Important properties of transfer functions 12. Given a causal, BIBO stable system with impulse re- sponse g ( n ) • Z-transform of g ( n ) , namely G ( z ) , will have poles inside unit circle g ( n ) is a causal sequence • G ( z ) = N ( z ) D ( z ) with – N ( z ) is a polynomial of degree n – D ( Z ) is a polynomial of degree m • n ≤ m 12 Digital Control Kannan M. Moudgalya, Autumn 2007

Z-transform Theorems - Linearity 13. Given the following Z-transform pairs, u 1 ( n ) ↔ U 1 ( z ) , u 2 ( n ) ↔ U 2 ( z ) , the following relation, with arbitrary α , β , holds: Z [ α { u 1 ( n ) } + β { u 2 ( n ) } ] = αU 1 ( z ) + βU 2 ( z ) 13 Digital Control Kannan M. Moudgalya, Autumn 2007

Example 1 - Linearity 14. Find the Z-transform of u 1 ( n ) = δ ( n ) − 3 δ ( n − 2) : ∞ ∞ δ ( n ) z − n − 3 � � δ ( n − 2) z − n U 1 ( z ) = n = −∞ n = −∞ ∀ z − 1 finite = 1 − 3 z − 2 14 Digital Control Kannan M. Moudgalya, Autumn 2007

Z-transform - Shifting 15. ∞ u ( n + d ) z − n � Z [ u ( n + d )] = n = −∞ ∞ u ( n + d ) z − ( n + d ) = z d � n = −∞ = z d U ( z ) 15 Digital Control Kannan M. Moudgalya, Autumn 2007

Z-transform - Shifting 16. Example: If { u ( n ) } ↔ U ( z ) , then { u ( n + 3) } ↔ z 3 U ( z ) { u ( n − 2) } ↔ z − 2 U ( z ) 16 Digital Control Kannan M. Moudgalya, Autumn 2007

Initial value, theorem for causal signals 17. z →∞ U ( z ) = u (0) lim 17 Digital Control Kannan M. Moudgalya, Autumn 2007

Final value theorem for causal signals 18. • Under the conditions – U ( z ) converges for all | z | > 1 , – if all poles of U ( z )(1 − z − 1 ) are inside unit circle, z → 1 (1 − z − 1 ) U ( z ) k →∞ u ( k ) = lim lim 18 Digital Control Kannan M. Moudgalya, Autumn 2007

Examples for Final Value Theorem 19. Using the final value theorem, find the steady state value of (0 . 5 n − 0 . 5)1( n ) and verify. z − 0 . 5 − 0 . 5 z z (0 . 5 n − 0 . 5)1( n ) ↔ z − 1 | z | > 1 n →∞ LHS = − 0 . 5 lim 0 . 5 z z → 1 ( z − 1) RHS = − lim lim z − 1( z − 1) z → 1 = − 0 . 5 19 Digital Control Kannan M. Moudgalya, Autumn 2007

Examples for Final Value Theorem 20. Is it possible to use the final value theorem on 2 n 1( n ) ? z 2 n 1( n ) ↔ z − 2 | z | > 2 • Since RHS is valid only for | z | > 2 , the theorem cannot even be applied. • In the LHS also, there is a pole outside the unit cir- cle thereby violating the conditions of the theorem. 20 Digital Control Kannan M. Moudgalya, Autumn 2007

Z-transform of Convolution 21. If u ( n ) ↔ U ( z ) g ( n ) ↔ G ( z ) then, g ( n ) ∗ u ( n ) ↔ G ( z ) U ( z ) Recall the motivation slide for Z-transform. 21 Digital Control Kannan M. Moudgalya, Autumn 2007

Z-transform of Discrete State Space Systems 22. x ( n + 1) = Ax ( n ) + Bu ( n ) x (0) = x 0 Invalid for n = − 1 : x (0) = Ax ( − 1) + Bu ( − 1) = 0 � = x 0 The fact that it is not valid for n < 0 is not explicitly stated. But if we write it as x ( n + 1) = Ax ( n ) + Bu ( n ) + δ ( n + 1) x 0 and assume initial rest, all variables are zero until n = 0 , problem is solved. 22 Digital Control Kannan M. Moudgalya, Autumn 2007

Z-transform of Discrete State Space Systems 23. Z-transform of x ( n + 1) = Ax ( n ) + Bu ( n ) + δ ( n + 1) x 0 gives zX ( z ) = AX ( z ) + BU ( z ) + x 0 z ( zI − A ) X ( z ) = BU ( z ) + x 0 z X ( z ) = ( zI − A ) − 1 BU ( z ) + z ( zI − A ) − 1 x 0 Z-transform of y ( n ) = Cx ( n ) + Du ( n ) is Y ( z ) = CX ( z ) + DU ( z ) = C ( zI − A ) − 1 BU ( z ) + DU ( z ) + C ( zI − A ) − 1 zx (0) = [ C ( zI − A ) − 1 B + D ] U ( z ) + C ( zI − A ) − 1 zx (0) 23 Digital Control Kannan M. Moudgalya, Autumn 2007

Finding Transfer Function - an Example 24. Find the transfer function of � � � � 1 0 0 . 02 A = , B = 0 . 19801 0 . 9802 0 . 001987 � � C = 0 1 D = 0 , , G = c ( zI − A ) − 1 B � − 1 � � � � z − 1 0 0 . 02 � = 0 1 − 0 . 19801 z − 0 . 9802 0 . 001987 � � 0 1 � z − 0 . 9802 � � � 0 0 . 02 = 0 . 19801 z − 1 0 . 001987 ( z − 1)( z − 0 . 9802) 24 Digital Control Kannan M. Moudgalya, Autumn 2007

Finding Transfer Function - an Example 25. � � 0 1 � z − 0 . 9802 � � � 0 0 . 02 G = 0 . 19801 z − 1 0 . 001987 ( z − 1)( z − 0 . 9802) � � 0 . 19801 z − 1 � � 0 . 02 = 0 . 001987 ( z − 1)( z − 0 . 9802) = 0 . 001987 z + 0 . 0019732 ( z − 1)( z − 0 . 9802) z + 0 . 9931 = 0 . 001987 ( z − 1)( z − 0 . 9802) 25 Digital Control Kannan M. Moudgalya, Autumn 2007

Finding Transfer Function - an Example 26. / / U p d a t e d ( 1 8 − 7 − 0 7 ) 1 / / 4 . 4 2 3 4 F = [0 0; 1 − 0.1]; G = [ 0 . 1 ; 0 ] ; 5 C = [0 1 ] ; dt = 0 . 2 ; 6 sys = syslin ( ’ c ’ ,F ,G,C) ; 7 sysd = dscr ( sys , dt ) ; 8 H = ss2tf ( sysd ) ; 26 Digital Control Kannan M. Moudgalya, Autumn 2007