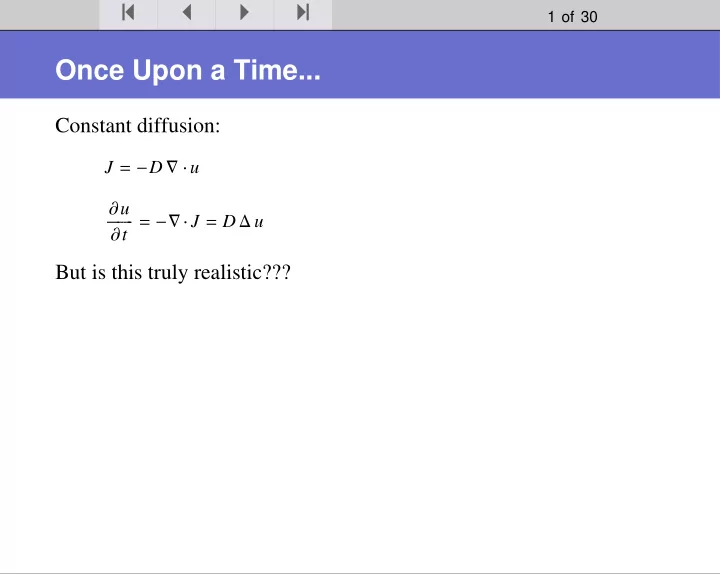
1 of 30 Once Upon a Time... Constant diffusion: J = - D u - PowerPoint PPT Presentation

« ≈ � � 1 of 30 Once Upon a Time... Constant diffusion: J = - D “ ÿ u ∑ u ÅÅÅÅÅÅÅÅÅÅ ∑ t = -“ ÿ J = D D u But is this truly realistic???

« ≈ � � 2 of 30 Problems With Constant Diffusion Any initial condition, even a point distribution, instantly "spreads out" to cover an infinite domain. Consider the one-dimensional case: l o o m o o ∑ t = D ∑ 2 u ∑ u ÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅ u H x , 0 L = d H x L n ∑ x 2 exp i y j z fl u H x , t L = j z j - z è!!!!!!!!!!!!! k { x 2 1 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅ 4 p D t 4 D t

« ≈ � � 3 of 30 Problems With Constant Diffusion 0.8 0.6 0.4 0.2 -10 -5 5 10

« ≈ � � 4 of 30 How Can We Improve This? Use a non-constant diffusion term: J = - D H u L “ ÿ u H x , t L ∑ t = -“ ÿ J = “ ÿ H D H u L “ ÿ u L ∑ u ÅÅÅÅÅÅÅÅÅÅ This makes intuitive sense - in an insect population, for example, we would expect very densely populated areas to diffuse outwards more quickly than sparsely populated areas.

« ≈ � � 5 of 30 Crap! Of course, now we need to figure out how to deal with non-constant diffusion in our solution.

« ≈ � � 6 of 30 A General Approach Rewrite our equation as ∑ t - “ ÿ H D H u L “ ÿ u L = 0 ∑ u ÅÅÅÅÅÅÅÅÅÅ We can consider this to be an example of a general class of functions of the form G H x , t , u , u x , u t , u xx , u xt , u tt L = 0

« ≈ � � 7 of 30 A General Approach The one-parameter family of stretching functions: êê = e a x x ê = e b t t êê = e c u u

« ≈ � � 8 of 30 A General Approach The one-parameter family of stretching functions: êê = e a x x ê = e b t t êê = e c u u a , b , and c are constants; e is a real parameter on some open interval that contains 1. Define G to be invariant if there exists a smooth function f H e L such that G H x ê L = f H e L G H x , t , u , u x , u t , u xx , u xt , u tt L ê , u êê , t êê , u êê x êê êê x êê êê êê , u ê , u êê x êê , u ê , u ê t êê t t x t

« ≈ � � 9 of 30 A General Approach Assume G is invariant. This gives us G H x êê L = f H e L G H x , t , u L ê , u êê , t G H e a x , e b t , e c u L = f H e L G H x , t , u L G H e a x , e b t , e c u L = f H e L H 0 L G H e a x , e b t , e c u L = 0 (Because G is homogenous.)

« ≈ � � 10 of 30 A General Approach Differentiate with respect to e : a x e a ∑ G ∑ x + b t e b ∑ G ∑ t + c u e c ∑ G ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅ ∑ u = 0 ÅÅÅ Set e = 1 (which we can do because we restrict e to a domain that contains 1): a x ∑ G ∑ x + b t ∑ G ∑ t + c u ∑ G ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅ ∑ u = 0 ÅÅÅ Clever people look at this and see that the transformation we want to use is u = t c ê b r H z L t a ê b x z = ÅÅÅÅÅÅÅÅ ÅÅÅ

« ≈ � � 11 of 30 A General Approach Verification of the transformation: a x ∑ G ∑ x + b t ∑ G ∑ t + c u ∑ G ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅ ∑ u = 0 ÅÅÅ a x ∑ G ∑ z ∑ z ∑ x + b t ∑ G ∑ z ∑ z ∑ t + c u ∑ G ∑ z ∑ z ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ∑ u = 0 ∑ z t a ê b , ∑ z 1 ÅÅÅÅÅÅÅÅÅ ∑ x = ÅÅÅÅÅÅÅÅ ÅÅÅ ÅÅÅÅÅÅÅÅÅ ∑ t = ∫

« ≈ � � 12 of 30 A General Approach What have we accomplished with all our fancy math? G H x , t , u , u x , u t , u xx , u xt , u tt L = 0 ó g H z , r , r ', r '' L = 0

« ≈ � � 13 of 30 A Specific Example Recall the problem we're actually working on: ∑ t = “ ÿ H D H u L “ ÿ u L ∑ u ÅÅÅÅÅÅÅÅÅÅ D H u L = D 0 J u N m ÅÅÅÅÅÅÅÅ u 0

« ≈ � � 14 of 30 A Specific Example Letting m = 1 gives us ∑ x J D 0 ∑ x N ∑ u ∑ t = ∑ u ∑ u ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ u 0 And because we're lazy, we'll assume D 0 ÅÅÅÅÅÅÅÅ u 0 = 1, so ∑ x J u ∑ u ∑ x N ∑ u ∑ t = ∑ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ The problem is now l ∑ x I u ∑ u ∑ x M o o m o o ∑ u ∑ ÅÅÅÅÅÅÅ ∑ t = ÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅ u H x , 0 L = d H x L n

« ≈ � � 15 of 30 A Specific Example Other assumptions: Since no organisms are being born or dying, we require for all t > 0 u H x , t L „ x = 1 ‡ ¶ -¶ and x Ø≤¶ u H x , t L = 0 lim

« ≈ � � 16 of 30 A Specific Example Check for invariance: G H x ê L = f H e L G H x , t , u , u x , u t , u xx , u xt , u tt L ê , u êê , t êê , u êê x êê êê x êê êê ê , u ê , u ê t êê , u êê x êê , u êê t t x t êê = e a x x ê = e b t t êê = e c u u êê J u êê N = e c - b ∑ u ∑ x J u ∑ u ∑ x N êê êê ∑ u ê - ∑ êê ∑ u ∑ t - e 2 c - 2 a ∑ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ∑ t ∑ x ∑ x We have invariance if c - b = 2 c - 2 a fl c = 2 a - b

« ≈ � � 17 of 30 A Specific Example u = t c ê b r H z L t a ê b x z = ÅÅÅÅÅÅÅÅ ÅÅÅ With our invariance condition, u = t H 2 a - b Lê b r H z L t a ê b x z = ÅÅÅÅÅÅÅÅ ÅÅÅ

« ≈ � � 18 of 30 A Specific Example Let's be clever: u H x , t L „ x = 1 ‡ ¶ -¶ r J x t a ê b N „ x = 1 t H 2 a - b Lê b ‡ ¶ ÅÅÅÅÅÅÅÅ ÅÅÅ -¶ r H z L „ z = 1 t H 3 a - b Lê b ‡ ¶ -¶ Time-independence requires b = 3 a Which simplifies the transformation to u = t - 1 ê 3 r H z L z = x t - 1 ê 3

« ≈ � � 19 of 30 A Specific Example l ∑ x I u ∑ u ∑ x M o o o o o ∑ u ∑ m ÅÅÅÅÅÅÅ ∑ t = ÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅ ï 3 H r r ' L ' + r + z r ' = 0 u = t - 1 ê 3 r H z L o o o o o n z = x t - 1 ê 3 This equation can be integrated to give 3 r r ' + z r = constant Take the constant to be zero; the solution is r H z L = A 2 - z 2 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅ 6

« ≈ � � 20 of 30 A Specific Example Use our conditions to clean it up: x Ø≤¶ u H x , t L = 0 lim means that l o o , † x § < A r H z L = m o o A 2 - z 2 ÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅ † x § > A n 6 0 And u H x , t L „ x = 1 ‡ ¶ -¶ means that 1 ê 3 A = J 9 2 N ÅÅÅÅÅ Now switch everything back to original coordinates.

« ≈ � � 21 of 30 A Specific Example l 6 t H A 2 t 2 ê 3 - x 2 L , † x § < A t 1 ê 3 o o u H x , t L = m o o ÅÅÅÅÅÅÅ 1 † x § > A t 1 ê 3 n 0 About time. Let's take a look!

« ≈ � � 22 of 30 A Specific Example - Pretty Pictures 0.35 0.3 0.25 0.2 0.15 0.1 0.05 -1 -0.5 0.5 1

« ≈ � � 23 of 30 A Specific Example The key feature of this solution is the sharp wave front at x f = A t 1 ê 3 This wave is moving with speed 3 A t - 2 ê 3 „ x f = 1 ÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅ ÅÅÅÅÅ „ t

« ≈ � � 24 of 30 Comparing Constant and Density-Dependent Diffusion at t = .1 0.8 0.6 0.4 0.2 -1 -0.5 0.5 1

« ≈ � � 25 of 30 Comparing Constant and Density-Dependent Diffusion at t = 10 0.08 0.06 0.04 0.02 -10 -5 5 10

« ≈ � � 26 of 30 What About the Not-Simple Case, You Ask? Recall that the general form is ∑ t = “ ÿ H D H u L “ ÿ u L ∑ u ÅÅÅÅÅÅÅÅÅÅ D H u L = D 0 J u N m ÅÅÅÅÅÅÅÅ u 0 and we assumed m = 1 for all the work we just did. Is there a general solution?

« ≈ � � 27 of 30 What About the Not-Simple Case, You Ask? Yes, and here it is: l o 1 ê m , † x § § r 0 l H t L l H t L J 1 - J r 0 l H t L N 2 N o o u H x , t L = m o o u 0 o ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ x ÅÅÅÅÅÅÅ † x § > r 0 l H t L n 0 Where 1 êH 2 + m L l H t L = J t N ÅÅÅÅÅÅÅ t 0 Q G I 1 2 M m + 3 ÅÅÅÅÅÅÅ ÅÅÅÅÅ 2 m p 1 ê 2 u 0 G I 1 2 D 0 H m + 2 L r 0 m + 1 M , t 0 = r 0 = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅ D 0 and n 0 are positive constants; Q is the initial density at the origin, and r 0 comes from requiring that the integral over the domain at all times be equal to Q .

« ≈ � � 28 of 30 Not-Simple Case, t = .1 and m = 1, 2, 3 1 0.8 0.6 0.4 0.2 -2 -1 1 2

« ≈ � � 29 of 30 Not-Simple Case, t = 10 and m = 1, 2, 3 0.4 0.3 0.2 0.1 -2 -1 1 2