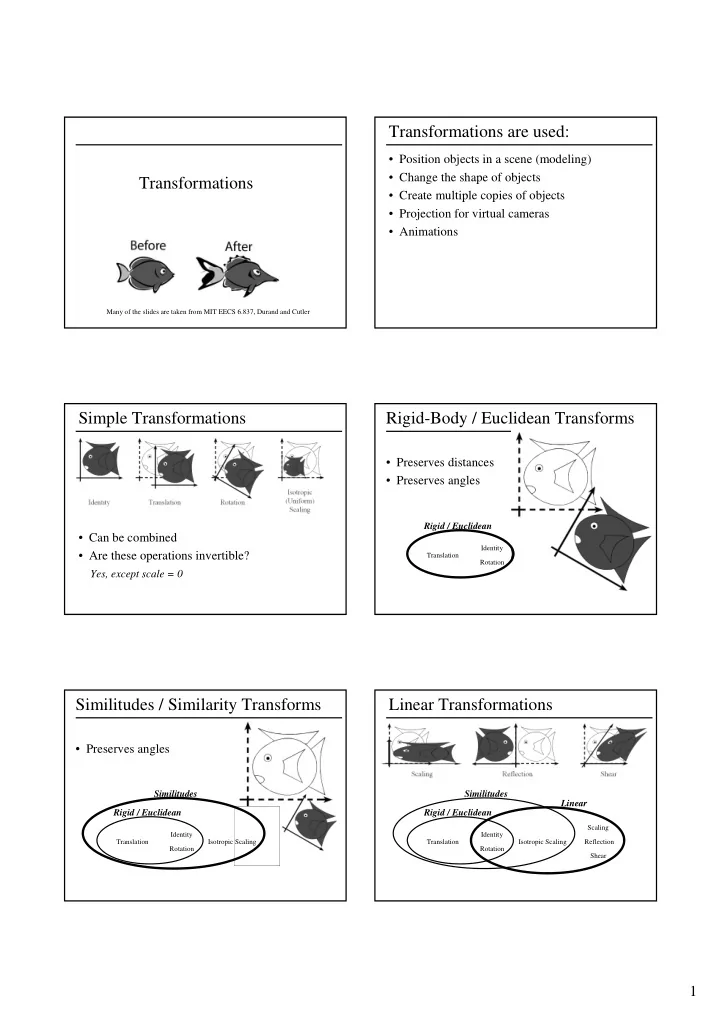
Transformations are used: Position objects in a scene (modeling) - PDF document

Transformations are used: • Position objects in a scene (modeling) • Change the shape of objects Transformations • Create multiple copies of objects • Projection for virtual cameras • Animations Many of the slides are taken from MIT EECS 6.837, Durand and Cutler Simple Transformations Rigid-Body / Euclidean Transforms • Preserves distances • Preserves angles Rigid / Euclidean • Can be combined Identity • Are these operations invertible? Translation Rotation Yes, except scale = 0 Similitudes / Similarity Transforms Linear Transformations • Preserves angles Similitudes Similitudes Linear Rigid / Euclidean Rigid / Euclidean Scaling Identity Identity Translation Isotropic Scaling Translation Isotropic Scaling Reflection Rotation Rotation Shear 1

Linear Transformations Affine Transformations • preserves • L(p + q) = L(p) + L(q) parallel lines • L(ap) = a L(p) Affine Similitudes Similitudes Linear Linear Rigid / Euclidean Rigid / Euclidean Scaling Scaling Identity Identity Translation Isotropic Scaling Reflection Translation Isotropic Scaling Reflection Rotation Rotation Shear Shear Projective Transformations Perspective Projection • preserves lines Projective Affine Similitudes Linear Rigid / Euclidean Scaling Identity Translation Isotropic Scaling Reflection Rotation Shear Perspective Outline How are Transforms Represented? • Assignment 0 Recap x’ = ax + by + c • Intro to Transformations y’ = dx + ey + f • Classes of Transformations • Representing Transformations x’ a b x c • Combining Transformations + = y f y’ d e • Change of Orthonormal Basis p’ = M p + t 2

Homogeneous Coordinates Homogeneous Coordinates • Add an extra dimension • Most of the time w = 1, and we can ignore it • in 2D, we use 3 x 3 matrices x’ a b c d x • In 3D, we use 4 x 4 matrices • Each point has an extra value, w y’ e f g h y = z’ i j k l z x’ a b c d x 1 0 0 0 1 1 y’ e f g h y = z’ i j k l z • If we multiply a homogeneous coordinate w’ m n o p w by an affine matrix , w is unchanged p’ = M p Homogeneous Visualization 3D Coordinate Systems • Right-handed coordinate system: • Divide by w to normalize (homogenize) z • W = 0? Point at infinity (direction) y y x • Left-handed coordinate system: (0, 0, 1) = (0, 0, 2) = … w = 1 (7, 1, 1) = (14, 2, 2) = … z (4, 5, 1) = (8, 10, 2) = … w = 2 x Translate ( t x , t y , t z ) 3D Transformations Translate( c,0,0 ) y • Why bother with the • In homogeneous coordinates, 3D extra dimension? p’ transformations are represented by 4x4 p Because now translations matrices. x can be encoded in the matrix! c • A point transformation is performed: 1 0 0 t x x x’ x’ x ’ a b c t x � � � � � � x 0 1 0 t y y y’ y’ = � � � � � � y ’ d e f t y z’ 0 0 1 t z z y z’ � � � � � � � z ’ g h i t z � � � � � � 1 0 0 0 0 1 1 z � � � � � � 1 0 0 0 1 1 � � � � � � 3

Scale ( s x , s y , s z ) Scale( s,s,s ) 3D Shearing p’ y • Isotropic (uniform) p 1 0 a b x x ay bz scaling: s x = s y = s z � � � � � � � � q’ � � � � � � q c 1 d 0 y cx y dz � � � � � � � � � x e f 1 0 z ex fy z � � � � � � � � � � � � � � 0 0 0 1 1 1 � � � � � � x’ s x 0 0 0 x • The change in each coordinate is a linear combination of all three. y’ 0 s y 0 0 y = • Transforms a cube into a general parallelepiped. z’ 0 0 s z 0 z 1 0 0 0 1 1 Rotation Rotation ZRotate( ) y p’ • About z axis x’ 0 0 0 x 1 • About y’ cos -sin 0 y 0 p = x axis: z’ sin cos 0 z 0 x z 1 0 0 0 1 1 0 0 x’ cos -sin x x’ cos 0 sin 0 x 0 0 y’ sin cos y = y’ 0 1 0 0 y • About 0 0 1 0 z’ z = y axis: z’ -sin 1 cos 0 z 0 0 0 1 1 1 1 0 0 0 1 1 Rotation 3D Rotation Rotate( k , ) y • To generate a rotation in 3D we have to • About ( k x , k y , k z ), a unit specify: vector on an arbitrary axis k – axis of rotation (2 d.o.f) (Rodrigues Formula) x z – amount of rotation (1 d.o.f) • Note, the axis passes through the origin. k x k x (1-c)+c k z k x (1-c)-k z s k x k z (1-c)+k y s 0 x x’ y k y k x (1-c)+k z s k z k x (1-c)+c k y k z (1-c)-k x s 0 y y’ = k z k x (1-c)-k y s k z k x (1-c)-k x s k z k z (1-c)+c 0 z z’ 1 0 0 0 1 1 where c = cos & s = sin z x 4

A counter-clockwise rotation about the z- axis: A counter-clockwise rotation about the x- axis: x ’ 1 0 0 0 x x ’ cos sin 0 0 x � � � � � � � � � � � � � � � � � � � � � y ’ 0 cos sin 0 y � � � � � � � y ’ sin cos 0 0 y � � � � � � � � � � � � � � � � � � z ’ 0 sin cos 0 z � � � � � � � � z ’ 0 0 1 0 z � � � � � � � � � � � � 1 0 0 0 1 1 � � � � � � � � � � � � 1 0 0 0 1 1 � � � � � � p ’ R ( ) p � � p ’ R ( ) p x � � z z z y y x x About Rotations A counter-clockwise rotation about the y- axis: x ’ cos 0 sin 0 x Inverse Rotation � � � � � � � � � � � � � � y ’ 0 1 0 0 y 1 � � � � � � � p R ( ) p ’ R ( ) p ’ � � � � � � z ’ sin 0 cos 0 z � � � � � � � � � � � � � � � 1 0 0 0 1 1 � � � � � � Composite Rotations p ’ R ( ) p � � y • R x , R y , and R z, can perform any rotation about an z axis passing through the origin. y x Rotation About an Arbitrary Axis Rotation About an Arbitrary Axis • Axis of rotation can be located at any point: 6 d.o.f. • Steps: • The idea : make the axis coincident with one of the – Translate P 0 to the origin. coordinate axes (z axis), rotate, and then transform – Make the axis coincident with the z -axis (for back. example): • Assume that the axis passes through the point p 0 . • Rotate about the x -axis into the xz plane. • Rotate about the y -axis onto the z -axis. z • Rotate as needed about the z -axis. p 0 • Apply inverse rotations about y and x . • Apply inverse translation. y x 5

Outline Rotation About an Arbitrary Axis • Assignment 0 Recap y y y • Intro to Transformations A p 0 B p 0 p 0 C • Classes of Transformations x x x • Representing Transformations z z z • Combining Transformations y y y • Change of Orthonormal Basis p 0 F E p 0 p 0 x x x z z z How are transforms combined? Non-commutative Composition Scale then Translate Scale then Translate: p' = T ( S p ) = TS p (5,3) (5,3) (2,2) (2,2) Scale(2,2) Translate(3,1) Scale(2,2) Translate(3,1) (1,1) (1,1) (3,1) (3,1) (0,0) (0,0) (0,0) (0,0) Use matrix multiplication: p' = T ( S p ) = TS p Translate then Scale: p' = S ( T p ) = ST p 0 0 0 1 3 2 0 2 3 TS = = 0 1 1 0 2 0 0 2 1 (8,4) (4,2) Translate(3,1) Scale(2,2) (6,2) 0 0 1 0 0 1 0 0 1 (1,1) (3,1) (0,0) Caution: matrix multiplication is NOT commutative! Non-commutative Composition Outline • Assignment 0 Recap Scale then Translate: p' = T ( S p ) = TS p • Intro to Transformations 1 0 3 2 0 0 2 0 3 • Classes of Transformations TS = 1 2 = 2 0 1 0 0 0 1 • Representing Transformations 0 0 1 0 0 1 0 0 1 • Combining Transformations Translate then Scale: p' = S ( T p ) = ST p • Change of Orthonormal Basis 2 0 0 1 0 3 2 0 6 ST = 1 = 0 2 0 0 1 0 2 2 0 0 1 0 0 1 0 0 1 6