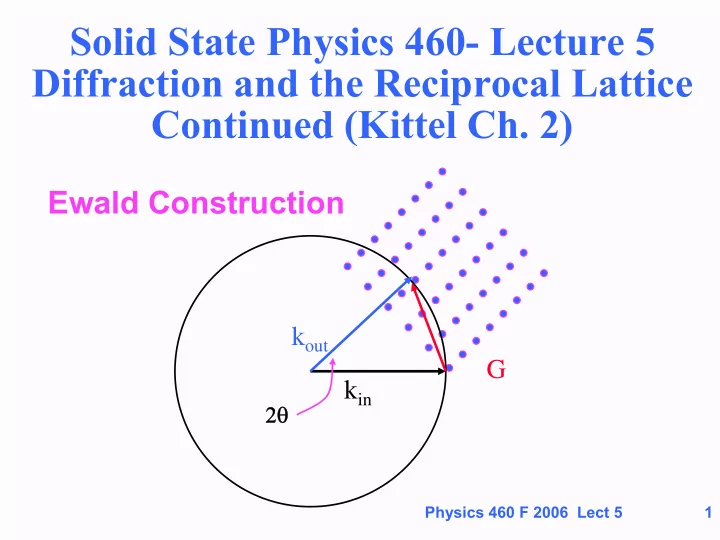
Solid State Physics 460- Lecture 5 Diffraction and the Reciprocal - PowerPoint PPT Presentation

Solid State Physics 460- Lecture 5 Diffraction and the Reciprocal Lattice Continued (Kittel Ch. 2) Ewald Construction k out G k in 2θ Physics 460 F 2006 Lect 5 1

Recall from previous lectures • Definition of a crystal – Lattice + Basis • Reciprocal lattice – Lattice in Fourier space (reciprocal space) • Diffraction from crystals – Bragg Condition – 2d sin θ = n λ • Diffraction and the reciprocal lattice • Today: • Diffraction and the reciprocal lattice continued – Ewald construction and the Brillouin Zone (BZ) Physics 460 F 2006 Lect 5 2

Recall from Summary: Real and Reciprocal lattices Lecture 3 • Crystal lattice of translations: Primitive vectors T (n 1 ,n 2 ,…) = n 1 a 1 + n 2 a 2 + n 3 a 3 • Reciprocal lattice: G (m 1 ,m 2 ,…) = m 1 b 1 + m 2 b 2 + m 3 b 3 , where b i . a j = 2 π δ ij , where δ ij = 1, δ ij = 0, i ≠ j • Any periodic function can be written f(r) = Σ G f G exp( i G . r) • Information about the basis for the actual crystal is in the values of the Fourier coefficients f G = (1/V cell ) ∫ cell d 3 r f(r) exp( - i G . r) Kittel Ch. 2 Physics 460 F 2006 Lect 5 3

Recall from Bragg Scattering Law Lecture 3 λ λ θ θ d 2 d sin θ • Condition for constructive interference (Diffraction): 2d sin θ = n λ • Maximum λ = 2d • Only waves with λ smaller than 2d can satisfy the Bragg scattering law for diffraction • For a typical crystal the maximum d ~ 0.1 – 1 nm, so that λ < ~ 0.1 – 1 nm Physics 460 F 2006 Lect 5 4

Recall from Scattering and Fourier Analysis Lecture 3 λ λ | k | = 2π/λ k in k out d • Note that k is a vector in reciprocal space with | k | = 2π/λ • The in and out waves have the form: exp( i k in . r - i ω t) and exp( i k out . r - i ω t) • If the incoming wave drives the electron density, which then radiates waves, the amplitude of the outgoing wave is proportional to: ∫ space dr n( r ) exp(i (k in - k out ) . r ) Physics 460 F 2006 Lect 5 5

Recall from Scattering and Fourier Analysis Lecture 3 λ ∆ k = G λ | k | = 2π/λ k in k out d • Define ∆ k = k in - k out • Then we know from Fourier analysis that (1/V cell ) ∫ cell d r n( r ) exp(- i ∆ k . r ) = n G only if ∆ k = G , where G is a reciprocal lattice vector • Otherwise the integral vanishes Note: These statements are for a perfect crystal of size → infinity. See prob. Kittel 2.4 for a finite crystal where the scattering is peaked at ∆ k = G with a finite width. Physics 460 F 2006 Lect 5 6

Recall from Elastic Scattering Lecture 3 λ ∆ k = G λ | k | = 2π/λ k in k out d • For elastic scattering (energy the same for in and out waves) 2 = k out 2 = | k in + G | 2 | k in | = | k out |, or k in • Then one arrives at the condition for diffraction: (using - G in expression above) G Is any one of the 2 k in . G = G 2 recip. lattice vectors • Equivalent to the Bragg condition – see next lecture Physics 460 F 2006 Lect 5 7

Ewald Construction G Is any one of the recip. lattice vectors k out • Condition for diffraction: G k in 2θ k out = k in + G and | 2 k in . G | = |G| 2 = 2 | k in | | G | sin θ • Why? ⇒ |G| = 2 | k in | | sin θ Discussed in class ( note sine function, not cosine) Physics 460 F 2006 Lect 5 8

Equivalent to Bragg Condition k out G k in • From last slide, 2θ | G | = 2 | k in | sin θ • But | k in | = 2 π / λ , and | G | = n (2 π /d), where d = spacing between planes (see homework, Kittel prob. 2-1) • ⇒ Bragg condition 2d sin θ = n λ Physics 460 F 2006 Lect 5 9

Geometric Construction of Diffraction Conditions b 2 - k out G • Recall k in – k out = G k in and |k in | = |k out | b 1 Consequence of condition • | 2 k in . G | = G 2 • The vector k in (and k out ) lies along the perpendicular bisecting plane of a G vector • One example is shown Physics 460 F 2006 Lect 5 10

Diffraction and the Brillouin Zone • Brillouin Zone - (BZ) - b 2 - k out the Wigner-Seitz cell of G the reciprocal lattice k in • Formed by perpendicular b 1 bisectors of G vectors Brillouin Zone • Special Role of Brillouin Zone • Diffraction occurs only for k on surface of Brillouin Zone • No diffraction occurs for any k inside the first Brillouin Zone • Important later in course Physics 460 F 2006 Lect 5 11

Comparison of diffraction from different lattices • The Bragg condition can also be written | G | = 2 | k in | sin θ ⇒ sin θ = (λ /4 π ) | G | • Thus the ratios of the sines of the angles for diffraction are given by: sin θ 1 / sin θ 2 = | G 1 | / | G 2 | • Each type of lattice has characteristic ratios the positions of diffraction peaks as a function of sin θ • Simple scaling with λ Physics 460 F 2006 Lect 5 12

Experimental Powder Pattern • Diffraction peaks at angles satisfying the Bragg condition • Experimental example Differences for imperfect powder averages Reciprocal Lattice units http:// www.uni-wuerzburg.de/mineralogie/crystal/teaching/teaching.html Physics 460 F 2006 Lect 5 13

Comparison of diffraction from different lattices • Ratios sin θ i / sin θ 0 = | G i | / | G 0 | , where θ 0 is the lowest angle peak (smallest G) 2 / G 0 • Easiest to give ratios of squares G i 2 Simple Cubic lattice (G in units of 2 π /a) G i ratio 2 G i 1,0,0 1 1 1,1,0 2 2 1,1,1 3 3 2,0,0 4 4 2,1,0 5 5 Physics 460 F 2006 Lect 5 14

Comparison of diffraction from different lattices - continued FCC real space lattice BCC real space lattice (G in units of 2 π /a) (G in units of 2 π /a) G i G i 2 ratio G i G i 2 ratio 1,1,1 3 1 1,1,0 2 1 2,0,0 4 4/3 2,0,0 4 2 2,2,0 8 8/3 2,1,1 6 3 3,1,1 11 11/3 2,2,0 8 4 2,2,2 12 4 3,1,0 10 5 4,0,0 16 1/3 2,2,2 12 6 Same ratios as Simple cubic! Physics 460 F 2006 Lect 5 15

Example of KCl, KBr (200) (220) (311) KBr • See Kittel Fig. 17 Ι (222) (111) • KCl and KBr have fcc structure – expect fcc “powder patterns” 2 θ • But KCl has a special feature • K+ and Cl- have the same number (200) (220) of electrons, they scatter x-rays (311) KCl almost the same ---- thus KCl has Ι • a pattern like simple cubic (222) (111) Why does this happen? 2 θ Physics 460 F 2006 Lect 5 16

Comparison of diffraction from different lattices - continued • Lower symmetry lattices • Example - Orthorhombic G = (n 1 2 π /a 1 , n 2 2 π /a 2 , n 3 2 π /a 3 ) • Lengths of G’s are in general not any special numbers since the a’s can be in any ratios • Many lines in diffraction pattern because of many different values of |G| • Hexagonal - length along c axis not related to lengths perpendicular to c axis Physics 460 F 2006 Lect 5 17

Fourier Analysis of the basis • The intensity of the diffraction at each G is proportional to the square of the amplitude of the Fourier component n G = (1/V cell ) ∫ cell dr n(r) exp(- i G . r) • It is also possible to regard the crystal density n(r) as a sum of atomic-like densities n atom (r - R i ), centered at point R i n(r) = ∑ all i n atom i (r - R i ) • Then also n G = ∑ i in cell ∫ space dr n atom i (r - R i ) exp(- i G . r) Cell Physics 460 F 2006 Lect 5 18

One atom per cell and Form Factor • Then one can set R i = 0 and n G is the Fourier transform of one atom density n G = ∫ space dr n atom (r) exp(- i G . r) n atom (r) |r| • Called Form Factor • Example in Kittel n G Values of |G| for a particular crystal |G| Physics 460 F 2006 Lect 5 19

More than one atom per cell • n G = ∑ i in cell ∫ space dr n atom i ( r - R i ) exp(- i G . r) = ∑ i in cell exp(- i G . R i ) ∫ space dr n atom i ( r - R i ) exp(- i G . (r - R i ) ) = ∑ i in cell exp(- i G . R i ) ∫ space dr n atom i ( r) exp(- i G . r) = ∑ i in cell exp(- i G . R i ) n G atom i • Interpretation: Structure Factor = atom i x phase factor exp(- iG . R i ) Form factor n G for each atom in unit cell Physics 460 F 2006 Lect 5 20

Structure factor • Often the basis contains more than one atom that is same element, e.g., diamond structure atom i = n G • Then n G atom is the same for each i and n G = ∑ i in cell exp(- i G . R i ) n G atom i atom ∑ i in cell exp(- i G . R i ) = n G • Define “pure” structure factor G = (1/N cell ) ∑ i in cell exp(- i G . R i ) S 0 where N cell = number of atoms in cell • Then n G = N 0 S 0 G n G atom NOTE - Kittel defines n G to be the “structure factor” Physics 460 F 2006 Lect 5 21

Body Centered Cubic viewed as Simple Cubic with 2 points per cell G = (1/2) ∑ i =1,2 exp(- i G . R i ) S 0 = (1/2) ( 1 + exp(- i G . R 2 ) = (1/2) exp(- i G . R 2 /2) a 3 [exp( i G . R 2 /2) + exp(- i G . R 2 /2) ] = exp(- i G . R 2 /2) cos ( G . R 2 /2) a 2 Result: If G = (v 1 v 2 v 3 ) 2 π /a a 1 |S 0 G | = 1 if sum of integers a is even Points at R 1 = (0,0,0) ; | S 0 G | = 0 if sum is odd R 2 = (1,1,1) a/2 Same as we found before! FCC reciprocal lattice Physics 460 F 2006 Lect 5 22