
Simple and Practical Algorithm for the Sparse Fourier Transform Haitham Hassanieh Piotr Indyk Dina Katabi Eric Price MIT 2012-01-19 Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 1 / 19
Outline Introduction 1 Algorithm 2 Experiments 3 Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 2 / 19
The Dicrete Fourier Transform Discrete Fourier transform: given x ∈ C n , find � x j ω ij � x i = Fundamental tool ◮ Compression (audio, image, video) ◮ Signal processing ◮ Data analysis ◮ ... FFT: O ( n log n ) time. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 4 / 19
Sparse Fourier Transform Often the Fourier transform is dominated by a small number of “peaks” ◮ Precisely the reason to use for compression. If most of mass in k locations, can we compute FFT faster? Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 5 / 19
Previous work Boolean cube: [KM92], [GL89]. What about C ? [Mansour-92]: k c log c n . Long list of other work [GGIMS02, AGS03, Iwen10, Aka10] Fastest is [Gilbert-Muthukrishnan-Strauss-05]: k log 4 n . ◮ All have poor constants, many logs. ◮ Need n / k > 40,000 or ω ( log 3 n ) to beat FFTW. ◮ Our goal: beat FFTW for smaller n / k in theory and practice. ◮ Result: n / k > 2 , 000 or ω ( log n ) to beat FFTW. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 6 / 19
Our result Simple, practical algorithm with good constants. √ kn log 3 / 2 n ) time. Compute the k -sparse Fourier transform in O ( Get � x ′ with approximation error ∞ ≤ 1 � � x ′ − � x � 2 x k � 2 k � � x − � 2 If � x is sparse, recover it exactly. Caveats: ◮ Additional � x � 2 / n Θ( 1 ) error. ◮ n must be a power of 2. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 7 / 19
Structure of this section If � x is k -sparse with known support S , find � x S exactly in O ( k log 2 n ) time. √ x approximately in � In general, estimate � O ( nk ) time. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 9 / 19
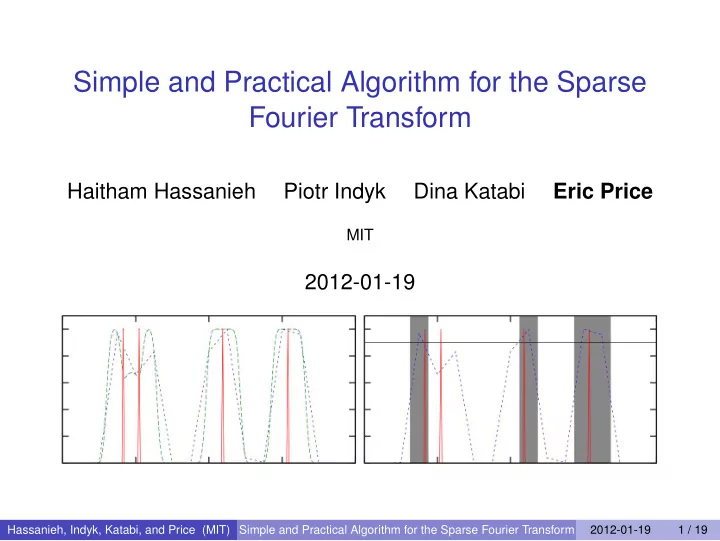
Intuition Original signal (time) Original signal (freq) n -dimensional DFT Cutoff signal (time) Cutoff signal (freq) n -dimensional DFT of first B terms. Cutoff signal (time) Cutoff signal, subsampled (freq) B -dimensional DFT of first B terms. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 10 / 19
Framework Cutoff signal (time) Cutoff subsampled signals (freq) “Hashes” into B buckets in B log B time. Issues: ◮ “Hashing” needs a random hash function ⋆ Access x ′ t = ω − at x σ t , so � x ′ t = � x σ − 1 t + a [GMS-05] ◮ Collisions ⋆ Have B > 4 k , repeat O ( log n ) times and take median. [Count-Sketch, CCF02] ◮ Leakage ◮ Finding the support. [Porat-Strauss-12], talk at 9:45am. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 11 / 19
Leakage Cutoff signal (time) Cutoff, subsampled signals (freq) � 1 i < B Let F i = be the “boxcar” filter. (Used in 0 otherwise [GGIMS02,GMS05]) Observe DFT ( F · x , B ) = subsample ( DFT ( F · x , n ) , B ) = subsample ( � F ∗ � x , B ) . DFT � F of boxcar filter is sinc, decays as 1 / i . Need a better filter F ! Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 12 / 19
Filters Filter (time) Filter (freq) 2.0 25 20 1.5 15 1.0 10 0.5 5 0.0 0 0 20 40 60 80 100 Bin Observe subsample ( � F ∗ � x , B ) in O ( B log B ) time. Needs for F : ◮ supp ( F ) ∈ [ 0 , B ] F | < δ = 1 / n Θ( 1 ) except “near” 0. ◮ | � ◮ � F ≈ 1 over [ − n / 2 B , n / 2 B ] . Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 13 / 19
Filters Filter (time) Filter (freq) 1.0 18 16 0.8 14 12 0.6 10 8 0.4 6 4 0.2 2 0.0 0 0 20 40 60 80 100 Bin Observe subsample ( � F ∗ � x , B ) in O ( B log B ) time. Needs for F : ◮ supp ( F ) ∈ [ 0 , B ] F | < δ = 1 / n Θ( 1 ) except “near” 0. ◮ | � ◮ � F ≈ 1 over [ − n / 2 B , n / 2 B ] . Gaussians: � ◮ Standard deviation σ = B / log n � ◮ DFT has � σ = ( n / B ) log n ◮ Nontrivial leakage into O ( log n ) buckets. ◮ But likely trivial contribution to correct bucket. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 13 / 19
Filters Filter (time) Filter (freq) 1.0 80 70 0.8 60 50 0.6 40 0.4 30 20 0.2 10 0.0 0 0 50 100 150 200 Bin Observe subsample ( � F ∗ � x , B ) in O ( B log B ) time. Needs for F : ◮ supp ( F ) ∈ [ 0 , B log n ] ◮ | � F | < δ = 1 / n Θ( 1 ) except “near” 0. ◮ � F ≈ 1 over [ − n / 2 B , n / 2 B ] . Gaussians: � � ◮ Standard deviation σ = ✘✘✘✘ ✘ B / log n B · log n � � ✘ ◮ DFT has � σ = ✘✘✘✘✘ ( n / B ) log n ( n / B ) / log n ◮ Nontrivial leakage into 0 buckets. ◮ But likely trivial contribution to correct bucket. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 13 / 19
Filters Filter (time) Filter (freq) 1.0 80 70 0.8 60 50 0.6 40 0.4 30 20 0.2 10 0.0 0 0 50 100 150 200 Bin � Let G be Gaussian with σ = B log n H be box-car filter of length n / B . Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 14 / 19
Filters Filter (time) Filter (freq) 0.10 1.2 0.08 1.0 0.06 0.8 0.04 0.6 0.02 0.4 0.00 0.2 0.02 0.0 0 50 100 150 200 Bin � Let G be Gaussian with σ = B log n H be box-car filter of length n / B . Use � F = � G ∗ H . ◮ F = G · � H , so supp ( F ) ⊂ [ 0 , B log n ] . F | < 1 / n Θ( 1 ) outside − n / B , n / B . ◮ | � F | = 1 ± 1 / n Θ( 1 ) within n / 2 B , n / B . ◮ | � Hashes correctly to one bucket, leaks to at most 1 bucket. Replace Gaussians with “Dolph-Chebyshev window functions”: factor 2 improvement. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 14 / 19
Algorithm to estimate � x S For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Algorithm to estimate � x S For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Algorithm to estimate � x S For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Algorithm to estimate � x S For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Algorithm in general For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Algorithm in general For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. To find S : choose all that map to the top 2 k values. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Algorithm in general For O ( log n ) different permutations of � x , compute subsample ( � F ∗ � x , B ) . Estimate each x i as median of values it maps to. To find S : choose all that map to the top 2 k values. nk / B candidates to update at each iteration: total √ ( nk nk log 3 / 2 n B + B log n ) log n = time. Hassanieh, Indyk, Katabi, and Price (MIT) Simple and Practical Algorithm for the Sparse Fourier Transform 2012-01-19 15 / 19
Recommend
More recommend