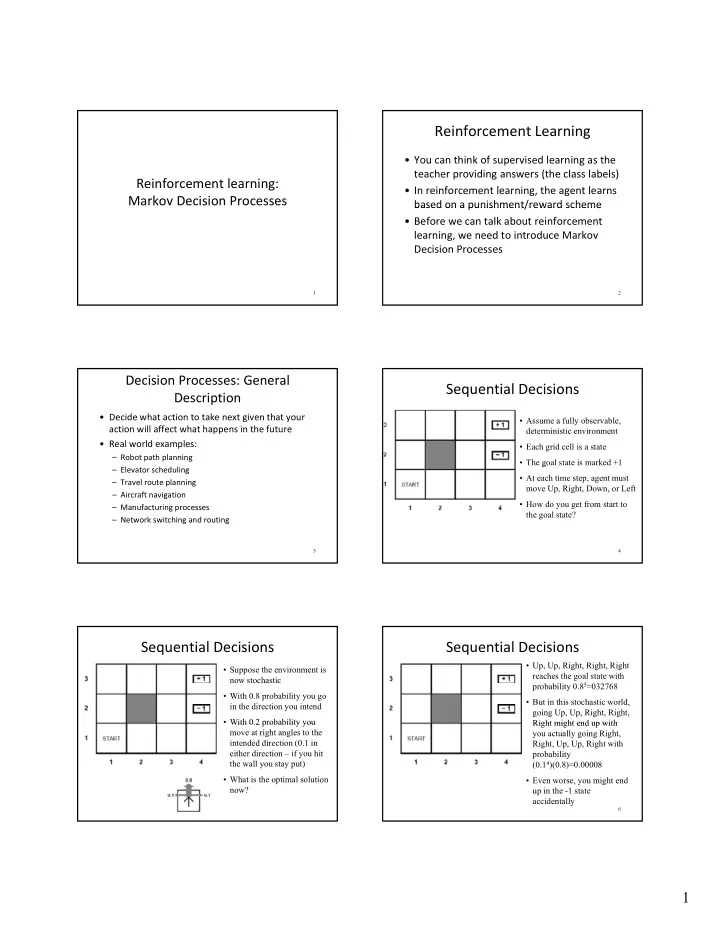
Reinforcement Learning You can think of supervised learning as the - PDF document

Reinforcement Learning • You can think of supervised learning as the teacher providing answers (the class labels) Reinforcement learning: • In reinforcement learning, the agent learns Markov Decision Processes based on a punishment/reward scheme based on a punishment/reward scheme • Before we can talk about reinforcement learning, we need to introduce Markov Decision Processes 1 2 Decision Processes: General Sequential Decisions Description • Decide what action to take next given that your • Assume a fully observable, action will affect what happens in the future deterministic environment • Real world examples: • Each grid cell is a state – Robot path planning • The goal state is marked +1 g – Elevator scheduling • At each time step, agent must – Travel route planning move Up, Right, Down, or Left – Aircraft navigation • How do you get from start to – Manufacturing processes the goal state? – Network switching and routing 3 4 Sequential Decisions Sequential Decisions • Up, Up, Right, Right, Right • Suppose the environment is reaches the goal state with now stochastic probability 0.8 5 =032768 • With 0.8 probability you go • But in this stochastic world, in the direction you intend going Up, Up, Right, Right, • With 0 2 probability you With 0.2 probability you Right might end up with Right might end up with move at right angles to the you actually going Right, intended direction (0.1 in Right, Up, Up, Right with either direction – if you hit probability the wall you stay put) (0.1 4 )(0.8)=0.00008 • What is the optimal solution • Even worse, you might end now? up in the -1 state accidentally 6 1

Transition Model Markov Property Example Suppose • Transition model: a specification of the outcome s 2 s 3 probabilities for each action in each possible state s 0 = (1,1), s 1 = (1,2), s 2 = (1,3) • T( s , a , s’ ) = probability of going to state s’ if you are in s 1 state s and do action a • The transitions are Markovian ie. the probability of If I go right from state s 2 , the s 0 s 2 reaching state s from s depends only on s and not on the reaching state s’ from s depends only on s and not on the probability of going to s 3 only history of earlier states (aka The Markov Property) depends on the fact that I am at • Mathematically: state s 2 and not the entire state Suppose you visited the following states in chronological history {s 0 , s 1 , s 2 } order: s 0 , …, s t P(s t+1 | a, s 0 , …, s t ) = P(s t+1 | a, s t ) 7 8 The Reward Function Utility Function Example R(4,3) = +1 (Agent wants to get here) • Depends on the sequence of states (known R(4,2) = ‐ 1 (Agent wants to avoid this as the environment history) R(s) = ‐ 0.04 (for all other states) • At each state s , the agent receives a reward U(s 1 , …, s n ) = R(s 1 ) + … + R(s n ) R(s) which may be positive or negative (but R(s) which may be positive or negative (but must be bounded) If the states an agent goes through • For now, we’ll define the utility of an are Up, Up, Right, Right, Right, the environment history as the sum of the utility of this environment history is: -0.04-0.04-0.04-0.04-0.04+1 rewards received 9 10 Utility Function Example Markov Decision Process If there’s no uncertainty, then the agent would find The specification of a sequential decision problem the sequence of actions that maximizes the sum of for a fully observable environment with a the rewards of the visited states Markovian transition model and additive rewards is called a Markov Decision Process (MDP) A MDP h An MDP has the following components: th f ll i t 1. A finite set of states S along with an initial state S 0 2. A finite set of actions A 3. Transition Model: T(s, a, s’) = P( s’ | a, s ) 4. Reward Function: R(s) 11 12 2

Solutions to an MDP A Policy • Why is the following not a satisfactory • Policy: mapping from a state to an action solution to the MDP? • Need this to be defined for all states so [1,1] ‐ Up that the agent will always know what to do [1,2] ‐ Up [ , ] p • Notation: • Notation: [1,3] ‐ Right – π denotes a policy [2,3] ‐ Right – π (s) denotes the action recommended by the [3,3] ‐ Right policy π for state s 13 14 Optimal Policy Optimal Policy Example • There are obviously many different policies for an MDP R(s)=-0.04 • Some are better than others. The “best” one is called the optimal policy π * (we will define best more precisely in later slides) • Note: every time we start at the initial state and execute a policy we get a different environment history (due to the policy, we get a different environment history (due to the stochastic nature of the environment) • This means we get a different utility every time we execute a policy • Need to measure expected utility ie. the average of the utilities of the possible environment histories generated by the policy Notice the tradeoff between risk and reward! 15 16 Roadmap for the Next Few Slides Finite/Infinite Horizons • Finite horizon: fixed time N after which nothing We need to describe how to compute matters (think of this as a deadline) optimal policies • Suppose our agent starts at (3,1), R(s)= ‐ 0.04, and N=3. Then to get to the +1 state, agent must go 1. Before we can do that, we need to define up. the utility of a state the utility of a state • If N=100, agent can take the safe route around If N 100 t t k th f t d 2. Before we can do (1), we need to explain stationarity assumption 3. Before we can do (2), we need to explain finite/infinite horizons 17 18 3

Nonstationary Policies Utility of a State Sequence • Nonstationary policy: the optimal action in a Under stationarity, there are two ways to assign given state changes over time utilities to sequences: • With a finite horizon, the optimal policy is 1. Additive rewards: The utility of a state sequence nonstationary is: • With an infinite horizon there is no incentive to • With an infinite horizon, there is no incentive to U(s 0 , s 1 , s 2 , …) = R(s 0 ) + R(s 1 ) + R(s 2 ) + … behave differently in the same state at different 2. Discounted rewards: The utility of a state times sequence is: • With an infinite horizon, the optimal policy is U(s 0 , s 1 , s 2 , …) = R(s 0 ) + γ R(s 1 ) + γ 2 R(s 2 ) + … stationary • We will assume infinite horizons Where 0 ≤ γ ≤ 1 is the discount factor 19 20 The Discount Factor Utilities We assume infinite horizons. This means that if the • Describes preference for current rewards over agent doesn’t get to a terminal state, then future rewards environmental histories are infinite, and utilities with • Compensates for uncertainty in available time additive rewards are infinite. How do we deal with this? (models mortality) Discounted rewards makes utility finite. • Eg Being promised $10000 next year is only • Eg. Being promised $10000 next year is only Assuming largest possible reward is R max and γ < 1, A i l t ibl d i R d 1 worth 90% of being promised $10000 now • γ near 0 means future rewards don’t mean ∞ ∑ = γ ( , , ,...) t ( ) U s s s R s anything 0 1 2 t = 0 t • γ = 1 makes discounted rewards equivalent to ∞ ∑ R additive rewards ≤ γ = max t R max − γ ( 1 ) = 0 t 21 22 The Optimal Policy Computing Optimal Policies • Given a policy π , we write the expected • A policy π generates a sequence of states sum of discounted rewards obtained as: • But the world is stochastic, so a policy π has ⎡ ∑ ∞ ⎤ a range of possible state sequences, each γ π ( ) | t E ⎢ R s ⎥ t of which has some probability of occurring of which has some probability of occurring ⎣ ⎣ = 0 ⎦ ⎦ 0 t t • The value of a policy is the expected sum of • An optimal policy π * is the policy that discounted rewards obtained maximizes the expected sum above ⎡ ∞ ⎤ ∑ π * = γ π arg max ( ) | t E ⎢ R s ⎥ t ⎣ ⎦ π = 0 t 23 24 4

The Optimal Policy Rewards vs Utilities • For every MDP, there exists an optimal policy • What’s the difference between R(s) the • There is no better option (in terms of expected reward for a state and U(s) the utility of a sum of rewards) than to follow this policy state? • How do you calculate this optimal policy? Can’t – R(s) – the short term reward for being in s ( ) g evaluate all policies…too many of them – U(s) – The long ‐ term total expected reward for • First, need to calculate the utility of each state the sequence of states starting at s (not just • Then use the state utilities to select an optimal the reward for state s) action in each state 25 26 Utilities in the Maze Example Utilities in the Maze Example Start at state (1,1). Let’s Start at state (1,1). Let’s suppose we choose the choose the action Up. action Up. Prob of moving right U(1,1) = R(1,1) + ... U(1,1) = R(1,1) + 0.8*U(1,2) + 0.1*U(2,1) + 0.1*U(1,1) Reward for current state Prob of moving up Prob of moving left (into the wall) and staying put 27 Utilities in the Maze Example The Utility of a State If we choose action a at state s, expected future rewards (discounted) are: ∑ = + γ ( ) ( ) ( , , ' ) ( ' ) U s R s T s a s U s ' s Now let’s throw in the discounting factor Reward at current state s Probability of moving from state s to state s’ U(1,1) = R(1,1) + γ * 0.8*U(1,2) + γ * 0.1*U(2,1) + by doing action a γ * 0.1*U(1,1) Expected sum of future Expected sum of future discounted rewards discounted rewards starting at state s starting at state s’ 29 5