MontyHall MontyHall Conditional Conditional Probability - PowerPoint PPT Presentation

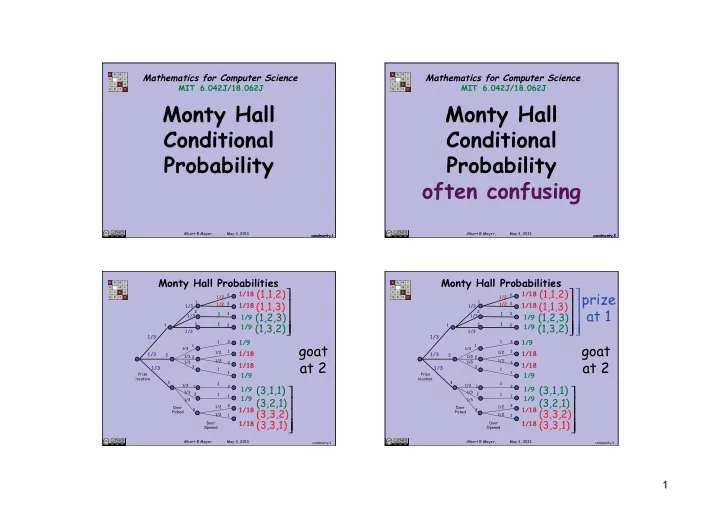
Mathematics for Computer Science Mathematics for Computer Science MIT 6.042J/18.062J MIT 6.042J/18.062J Monty Hall Monty Hall Conditional Conditional Probability Probability often confusing Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.1 condmonty.1 condmonty.2 condmonty.2 Monty Hall Probabilities Monty Hall Probabilities    (1,1,2) (1,1,2) 1/18 1/18 2 2 prize 1/2 1/2    1 1 1/2 3 1/18 (1,1,3) 1/2 3 1/18 (1,1,3) 1/3 1/3 2  2   at 1 1 3 1 3 1/3 (1,2,3) 1/3 (1,2,3) 1/9 1/9    3 1 3 1 1 2 1/9 (1,3,2)  1 2 1/9 (1,3,2)   1/3 1/3 1/3 1/3 1/9 1/9 1 3 1 3 1 1 goat goat 1/3 1/3 1 1 1/18 1/18 1/2 1/2 1/3 1/3 2 2 1/3 1/3 2 2 1/2 1/2 1/3 1/3 3 at 2 3 at 2 1/18 1/18 3 3 1/3 1/3 1 1 1 1 Prize 1/9 Prize 1/9 location location 3 3 1 1 1/3 1/3 1 2 1 2 1/9 (3,1,1)  1/9 (3,1,1)  1/3 1/3 2 2 1 1 1 1 1/9 1/9   1/3 (3,2,1) 1/3 (3,2,1) 2 2 1/2 1/2 Door Door 1/18 1/18 3 3   (3,3,2) (3,3,2) Picked Picked 1/2 1/2 1 1   1/18 (3,3,1) 1/18 (3,3,1) Door  Door  Opened Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.3 condmonty.4 1

Monty Hall Probabilities Conditional Probability : Monty Hall  (1,1,2) 1/18 2 prize 1/2  1 1/2 3 (1,1,3) 1/18 1/3 2 at 1  1 3 (1,2,3) 1/3 1/9 Pr[ prize at 1 | goat at 2] 1  3 1 2 1/9 (1,3,2)  1/3 1/3 3 1/9 1 1 1/3 1 1/2 1/18 = 1 1/3 2 1/3 2 1/2 1/3 3 1/18 3 1/3 Really! 1 1 Prize 1/9 location 3 1 1/3 1 2 1/9 2 1/3 2 1 1 1/9 1/3 2 Door 1/2 1/18 3 Picked 1/2 1 1/18 Door Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.8 condmonty.5 condmonty.5 Monty Hall Probabilities Conditional Probability : Monty Hall  (1,1,2) ] 1/18 2 prize 1/2  1 1/2 3 1/18 (1,1,3) 1/3 2  at 1 1 3 1/3 (1,2,3) 1/9  Pr[ prize at 1 | Carol opens 2] 3 1 ] 1 2 1/9 (1,3,2)  1/3 1/3 1/9 1 3 1 Carol 1/3 1 1/18 1/2 1/3 = 1 2 1/3 2 1/2 1/3 3 1/18 opens 2 3 1/3 Likewise! 1 1 Prize 1/9 location 3 1 1/3 1 2 ] 1/9 (3,1,1) 2 1/3 2 1 1 1/9 1/3 2 1/2 Door 1/18 3 ] (3,3,2) Picked 1/2 1 1/18 Door Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.9 condmonty.10 condmonty.10 2

Monty Hall Probabilities Monty Hall Probabilities  ]  ] (1,1,2) (1,1,2) 1/18 1/18 2 2 1/2 1/2  ]  ] 1 1 1/2 3 (1,1,3) 1/2 3 (1,1,3) 1/18 1/18 1/3 1/3  2 2  1 1 3 3 1/3 1/9 1/3 1/9   1  1 3 3  1 2 1 2 1/9 1/9 goat goat 1/3 1/3 1/3 ] 1/3 ] (2,1,3) (2,1,3) 3 1/9 3 1/9 1 1 at 2 at 2 1 1 1/3 1/3 1 1 1/2 1/18 1/2 1/18 1/3 1/3 & 2 2 1/3 1/3 2 2 1/2 1/2 1/3 3 1/3 3 1/18 1/18 picked 1 picked 1 3 3 1/3 1/3 1 1 1 1 Prize 1/9 Prize 1/9 location location 3 ] 3 ] 1 1  1/3 (3,1,2) 1/3 (3,1,2) 1 2 1 2  1/9 1/9 1/3 1/3 2 1 2 1 1 1  1/9 1/9  1/3 1/3 2 2 Door 1/2 Door 1/2  1/18 1/18  3 3 Picked Picked 1/2 1/2 1 1     1/18 1/18 Door Door Opened Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.13 condmonty.14 Monty Hall Probabilities Conditional Probability : Monty Hall (1,1,2) 1/18 2 1/2 1 1/2 3 1/18 (1,1,3) 1/3 Pr[ prize at 1 | picked 1 & 2 1 3 1/3 1/9 3 1 1 2 1/9 goat goat at 2] 1/3 1/3 1/9 1 3 at 2 1 1/3 = 1 1 1/18 1/2 1/3 & 2 1/3 2 1/2 1/3 3 1/18 picked 1 3 1/3 Also! 1 1 Prize 1/9 location 2 3 1 1/3 (3,1,2) 1 2 1/9 1/3 2 1 1 1/9 1/3 2 1/2 Door 1/18 3 Picked 1/2 1 1/18 Door Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.15 condmonty.16 condmonty.16 3

Stick or Switch? Conditional Probability : Monty Hall Seems the contestant may as well So until now, we have stick , since the probabili ty is 1/2 been conditioning on given what he knows when he the wrong events —a chooses. Wait! contestant common blunder. knows more than what door he picked & where a goat is, Using the correct one: he knows what door Carol opened! Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.21 condmont .21 condmonty condmont y.22 .22 Monty Hall Probabilities Monty Hall Probabilities 1/18 (1,1,2) ] 1/18 (1,1,2) ]] 2 2 1/2 1/2 1/18 (1,1,3) ] 1/18 (1,1,3) ] 1 1 1/2 3 1/2 3 1/3 1/3 1/9 ] opened 2 2 2 1 3 1 3 1/3 1/3 1/9 3 1 3 1 1 2 1/9 1 2 1/9 1/3 1/3 1/9 (2,1,3) ] 1/9 (2,1,3) ] 1/3 1/3 1 3 1 3 1 1 1/3 1/3 1 1 1/18 1/18 1/2 1/2 1/3 1/3 2 2 1/3 1/3 2 2 1/2 1/2 1/3 1/3 3 3 1/18 1/18 picked 1 picked 1 3 3 1/3 1/3 1 1 1 1 Prize 1/9 Prize 1/9 location location 1/9 (3,1,2) ] 3 3 1/9 (3,1,2) ]] 1 1 1/3 1/3 1 2 1 2 1/3 1/3 2 2 1 1 1 1 1/9 1/9 1/3 1/3 ] 2 2 1/2 1/2 Door Door 1/18 1/18 3 3 Picked Picked 1/2 1/2 1 1 1/18 1/18 Door Door Opened Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.23 condmonty.24 4

Monty Hall Probabilities Monty Hall Probabilities ] ] ] ] (1,1,2) (1,1,2) 1/18 1/18 2 2 1/2 1/2 ] 1 1 1/2 3 (1,1,3) 1/2 3 1/18 1/18 1/3 1/3 2 2 1 1 3 3 1/3 1/9 1/3 1/9 ] opened 2 opened 2 1 1 3 3 1 2 1 2 1/9 1/9 1/3 1/3 1/3 ] 1/3 (2,1,3) 3 1/9 3 1/9 1 1 1 1 1/3 1/3 1 1 1/2 1/18 & 1/2 1/18 & 1/3 1/3 2 2 1/3 1/3 2 2 1/2 1/2 1/3 3 1/3 3 1/18 1/18 picked 1 picked 1 3 3 1/3 1/3 1 1 1 1 Prize 1/9 Prize 1/9 location location 3 ] 3 ] ] ] 1 1 1/3 (3,1,2) 1/3 (3,1,2) 1 2 1 2 1/9 1/9 1/3 1/3 2 1 2 1 1 1 1/9 1/9 1/3 1/3 2 ] 2 Door 1/2 Door 1/2 1/18 1/18 3 3 Picked Picked 1/2 1/2 1 1 1/18 1/18 Door Door Opened Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.25 condmonty.26 Monty Hall Probabilities Conditional Probability : Monty Hall (1,1,2) 1/18 2 1/2 1 1/2 3 1/18 1/3 2 1 3 1/3 1/9 opened 2 3 1 prize at 1 1 2 1/9 1/3 1/3 1/9 1 3 1 1/3 1 1/18 & 1/2 1/3 2 1/3 2 1/2 [ picked 1 & opened 2 ] = 1/3 3 1/18 picked 1 3 1/3 1 1 Prize 1/9 location { (1,1,2),(3,1,2) } 3 1 1/3 (3,1,2) 1 2 1/9 1/3 2 1 1 1/9 1/3 2 1/2 Door 1/18 3 Picked 1/2 1 1/18 Door Opened Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.27 condmonty.29 condmonty.29 5

Conditional Probability : Monty Hall Conditional Probability : Monty Hall Pr[ prize at 1 | picked 1 & Pr[ prize at 1 | picked 1 & opened 2] opened 2] 1 / 18 [ picked 1 & opened 2 ] = = { (1,1,2),(3,1,2) } 1 / 18 + 1 / 9 X X Pr=1/18 Pr=1/9 Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.30 condmonty.30 condmonty.31 condmonty.31 Stick or Switch? Conditional Probability : Monty Hall Pr[ prize at 1 | picked 1 & Pr[ prize at 1 | picked 1 & opened 2] opened 2] 1 / 18 = 1 1 / 18 = 1 = = 1 / 18 + 1 / 9 3 1 / 18 + 1 / 9 3 = Pr[sticking wins] = Pr[sticking wins] Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.32 condmonty.32 condmonty.33 condmonty.33 6

Switch! The 4 Step Method By conditioning on everything It’s easy to how so many the contestant knows, we’ve smart people get confused by finally confirmed what we Monty Hall. learned earlier: 2 Pr[switching wins] = 3 Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.34 condmont .34 condmonty.35 The 4 Step Method The 4 Step Method It’s easy to how so many It’s easy to how so many smart people get confused by smart people get confused by Monty Hall. Finding the right Monty Hall. Finding the right event to condition on can be event to condition on can be tricky. tricky. The 4 step method is a good fall back approach. Albert R Meyer, May 3, 2013 Albert R Meyer, May 3, 2013 condmonty.36 condmonty.37 7

MIT OpenCourseWare http://ocw.mit.edu 6.042J / 18.062J Mathematics for Computer Science Spring 20 15 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.