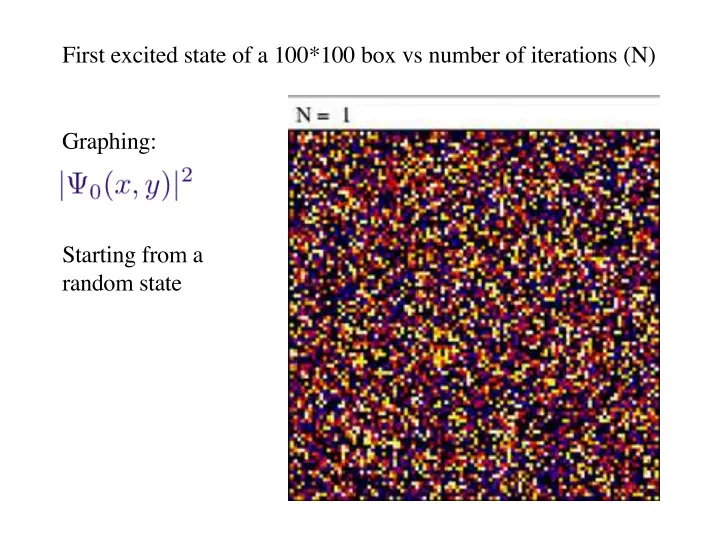
First excited state of a 100*100 box vs number of iterations (N) - PowerPoint PPT Presentation

First excited state of a 100*100 box vs number of iterations (N) Graphing: Starting from a random state

Second excited state of a 100*100 box vs number of iterations (N) Graphing: Starting from a random state

The first excited state should be doubly-degenerate Ø Lanczos only gives one state out of a degenerate multiplet Go back to the Krylov space If states k, j are degenerate, we have a term For any m, this vector points in the same direction in the subspace spanned by Acting with H cannot “ separate ” degenerate states Since the Lanczos basis spans the same Krylov space, we only get one state out of a degenerate multiplet of states Ø the particular linear combination depends on the initial state Numerical round-off errors can lead to apparent degeneracies (multiple copies of the same state). This indicates that the scheme breaks down as the basis becomes non-orthogonal.

Example in two dimensions: box with open boundaries (open corresponds to hard walls) Constructing State n stored in f1(nx*ny) labeling for 4*4 elements State constructed in f2(nx*ny) t = hopping (kinetic) matrix element - consider hopping into all boxes j subroutine hoperation(f1,f2) f2(:)=vpot(:)*f1(:) do j=1,nx*ny x=1+mod(j-1,nx) y=1+(j-1)/nx if (x.ne.1) f2(j-1)=f2(j-1)-t*f1(j) if (x.ne.nx) f2(j+1)=f2(j+1)-t*f1(j) if (y.ne.1) f2(j-nx)=f2(j-nx)-t*f1(j) if (y.ne.ny) f2(j+nx)=f2(j+nx)-t*f1(j) enddo

One step in the iteration of the a and b coefficients here m=n+1 if (m==1) then call hoperation(f0,f1) aa(0)=dot_product(f0,f1) f1=f1-aa(0)*f0 nn(1)=dot_product(f1,f1) else call hoperation(f1,f2) The method of aa(m-1)=dot_product(f1,f2)/nn(m-1) bb(m-2)=nn(m-1)/nn(m-2) constructing f2=f2-aa(m-1)*f1-bb(m-2)*f0 the normalized nn(m)=dot_product(f2,f2) states directly f0=f1 is very similar f1=f2 (program on-line) endif

The full basis and Hamiltonian construction Random initial state do i=1,n psi(i)=rand()-0.5d0 enddo norm=1.d0/sqrt(dot_product(psi,psi)) psi(:)=psi(:)*norm niter Lanczos steps and diagonalize Perform niter f0(:)=psi(:) nn(0)=1.d0 Do m=1,niter perform code on previous page enddo d(:)=aa(:) e(:)=sqrt(bb(:)) call diatri(niter,d,e,eig,states )

Calculation of the states In order to calculate states (wave functions) we have to perform another Lanczos procedure, since we have not saved all the states |f n > If we want the m-th lowest state, we transform with the m-th eigenvector obtained in the diagonalization. The eigenvectors are in the matrix states ; vec=states(:,m vec=states(:,m ) f0=psi f0=psi Normalized states psi=psi*vec(0) psi=psi*vec(0) call hoperation(n,f0,f1) call hoperation(n,f0,f1) f1=f1 f1=f1-aa(0)*f0 aa(0)*f0 psi=psi+vec(1)*f1/sqrt(nn(1)) psi=psi+vec(1)*f1/sqrt(nn(1)) do i=2,niter do i=2,niter-1 call hoperation(n,f1,f2) call hoperation(n,f1,f2) f2=f2-aa(i f2=f2 aa(i-1)*f1 1)*f1-bb(i bb(i-2)*f0 2)*f0 psi=psi+vec(i)*f2/sqrt(nn(i)) psi=psi+vec(i)*f2/sqrt(nn(i)) f0=f1 f0=f1 f1=f2 f1=f2 enddo enddo