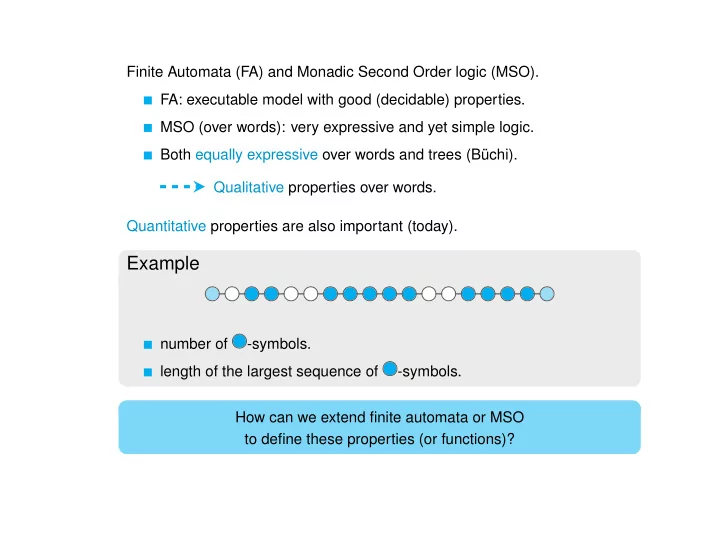
example
play

Example number of -symbols. length of the largest sequence of - PowerPoint PPT Presentation

Feb 03, 2023 •311 likes •630 views

Finite Automata (FA) and Monadic Second Order logic (MSO). FA: executable model with good (decidable) properties. MSO (over words): very expressive and yet simple logic. Both equally expressive over words and trees (Bchi). Qualitative

  1. Finite Automata (FA) and Monadic Second Order logic (MSO). FA: executable model with good (decidable) properties. MSO (over words): very expressive and yet simple logic. Both equally expressive over words and trees (Büchi). Qualitative properties over words. Quantitative properties are also important (today). Example number of -symbols. length of the largest sequence of -symbols. How can we extend finite automata or MSO to define these properties (or functions)?

  2. Weighted automata General automata framework to define quantitative properties over words. (Boolean) automata, Probabilistic automata, Distance automata, Multiplicity automata, etc... Extension of finite automata with weights from a fix semiring.

  3. Semiring (reminder) Definition A (commutative) semiring is an algebraic structure S = ( S , ⊕ , ⊙ , 0 , 1 ) where: ( S , ⊕ , 0 ) and ( S , ⊙ , 1 ) are commutative monoids, multiplication distributes over addition, and 0 ⊙ s = s ⊙ 0 = 0 for each s ∈ S . Example Natural numbers: ( N , + , ⋅ , 0 , 1 ) . Boolean: ({ true , false } , ∨ , ∧ , false , true ) . Min-plus: ( N ∞ , min , + , ∞ , 0 ) . Max-plus: ( N −∞ , max , + , −∞ , 0 ) .

  4. Weighted automata (definition) Fix a semiring S and a finite alphabet Γ . Definition A weighted automata over S and Γ is a tuple A = ( Γ , S , Q , E , I , F ) : E ∶ Q × Γ × Q → S is the transition relation ( p a / s � → q ), and I , F ∶ Q → S is the initial and final function. Semantics A run ρ of A over a 1 . . . a n ∈ Γ ∗ is: � → q 1 � → ⋯ a n / s n � → q n a 1 / s 1 a 2 / s 2 ρ = q 0 The weight of run ρ of A : n ⊙ weight ( ρ ) = I ( q 0 ) ⊙ s i ⊙ F ( q n ) i = 1 A defines the function ⟦ A ⟧ ∶ Γ ∗ → S : ⊕ ⟦ A ⟧( w ) = weight ( ρ ) ρ ∈ Run A ( w )

  5. Weighted automata (examples) Over ( N , + , ⋅ , 0 , 1 ) a , b / 1 a , b / 1 a / 3 f ( w ) = 3 ⋅ ∣ w ∣ a + 4 ⋅ ∣ w ∣ b b / 4 Over ( N ∞ , min , + , ∞ , 0 ) a / 1 a / 0 f ( w ) = min {∣ w ∣ a , ∣ w ∣ b } b / 0 b / 1 Over ( N −∞ , max , + , −∞ , 0 ) f ( w ) = maximum length of all infix sequences of b ’s a , b / 0 b / 1 a , b / 0 b / 1 a / 0

  6. What is a good logic to define quantitative properties? Weighted MSO (Droste & Gastin 2005) Disadvantages: Semantical definition of valid formulas. Inherits the undecidability results of weighted automata. We want a quantitative logic that: 1. has a simple and purely syntactical definition, 2. as expressive as weighted automata, and 3. with good decidability properties.

  7. We propose: Quantitative Monadic Second Order Logic (QMSO) 1. General framework for adding quantitative properties to any boolean logic. 2. Subfragments of QMSO capture different subclasses of WA. 3. Subfragments of QMSO with good decidability properties. More results in the paper: Evalution of QMSO with respect to counting complexity classes.

  8. Quantitative Monadic Second-Order Logic Cristian Riveros University of Oxford Stephan Kreutzer Technische Universität Berlin LICS 2013

  9. Outline QMSO and WA QMSO and subclasses of WA Beyond WA Conclusions

  10. Quantitative Monadic Second Order Logic (QMSO) For each w ∈ Γ ∗ , we represent w ∶ = ({ 1 , . . . , ∣ w ∣} , ≤ , { P a } a ∈ Γ ) . Syntax of QMSO [ S , Γ ] ∶ = P a ( x ) ∣ x ≤ y ∣ x ∈ X ∣ ϕ ∨ ϕ ∣ ¬ ϕ ∣ ∃ x . ϕ ∣ ∃ X . ϕ ϕ ∶ = ϕ ∣ s ∈ S ∣ θ ⊕ θ ∣ θ ⊙ θ ∣ Σ x . θ ∣ Π x . θ ∣ Σ X . θ θ Semantic of QMSO [ S , Γ ] if ( w , σ ) ⊧ ϕ ⟦ ϕ ⟧( w , σ ) ∶ = { 1 0 otherwise ⟦ s ⟧( w , σ ) ∶ = s ⟦ θ 1 ⊕ θ 2 ⟧( w , σ ) ∶ = ⟦ θ 1 ⟧( w , σ ) ⊕ ⟦ θ 2 ⟧( w , σ ) ⟦ Π x . θ ( x )⟧( w , σ ) ∶ = ⊙ ⟦ θ ( x )⟧( w , σ [ x → i ]) i ∈ dom ( w ) ∶ = ⊕ ⟦ θ ( X )⟧( w , σ [ X → I ]) ⟦ Σ X . θ ( X )⟧( w , σ ) I ⊆ dom ( w )

  11. Quantitative Monadic Second Order Logic (QMSO) The syntax of QMSO [ S , Γ ] depends on the semiring. Syntax of QMSO [( N , + , ⋅ , 0 , 1 ) , Γ ] ∶ = P a ( x ) ∣ x ≤ y ∣ x ∈ X ∣ ϕ ∨ ϕ ∣ ¬ ϕ ∣ ∃ x . ϕ ∣ ∃ X . ϕ ϕ ∶ = ϕ ∣ s ∈ N ∣ θ + θ ∣ θ ⋅ θ ∣ Σ x . θ ∣ Π x . θ ∣ Σ X . θ θ Syntax of QMSO [( N ∞ , min , + , ∞ , 0 ) , Γ ] P a ( x ) ∣ x ≤ y ∣ x ∈ X ∣ ϕ ∨ ϕ ∣ ¬ ϕ ∣ ∃ x . ϕ ∣ ∃ X . ϕ ϕ ∶ = ϕ ∣ s ∈ N ∞ ∣ min { θ, θ } ∣ θ + θ ∣ Min x . θ ∣ Σ x . θ ∣ Min X . θ ∶ = θ Syntax of QMSO [( N −∞ , max , + , −∞ , 0 ) , Γ ] P a ( x ) ∣ x ≤ y ∣ x ∈ X ∣ ϕ ∨ ϕ ∣ ¬ ϕ ∣ ∃ x . ϕ ∣ ∃ X . ϕ ϕ ∶ = ϕ ∣ s ∈ N −∞ ∣ max { θ, θ } ∣ θ + θ ∣ Max x . θ ∣ Σ x . θ ∣ Max X . θ θ ∶ =

  12. Examples of QMSO formulas Over ( N , + , ⋅ , 0 , 1 ) f ( w ) = 3 ⋅ ∣ w ∣ a + 4 ⋅ ∣ w ∣ b Σ x . ( 3 ⋅ P a ( x ) + 4 ⋅ P b ( x ) ) Over ( N ∞ , min , + , ∞ , 0 ) f ( w ) = min {∣ w ∣ a , ∣ w ∣ b } min { Σ x . P a ( x ) ↦ 1 , Σ x . P b ( x ) ↦ 1 } P a ( x ) ↦ 1 ∶ = min { P a ( x ) + 1 , ¬ P a ( x ) } . where Over ( N −∞ , max , + , −∞ , 0 ) f ( w ) = maximum length of all infix sequences of b ’s Max x . ( Σ y . interval b ( x , y ) ↦ 1 ) interval b ( x , y ) ∶ = x ≤ y ∧ ∀ z . ( x ≤ z ∧ z ≤ y ) → P b ( z ) . where

  13. Subfragments of QMSO 1. QMSO ( Op ) restricted to operators Op ⊆ {⊕ , ⊙ , Σ x , Π x , Σ X } . ⊕ = semiring addition ⊙ = semiring multiplication Σ x = first-order addition Π x = first-order multiplication Σ X = second-order addition Example Full QMSO ∶ = QMSO ( Σ X , Π x , Σ x , ⊕ , ⊙ )

  14. Subfragments of QMSO 1. QMSO ( Op ) restricted to operators Op ⊆ {⊕ , ⊙ , Σ x , Π x , Σ X } . 2. Alternation and Nesting of semiring quantifiers. Example QMSO ( Σ X Σ x Π x , ⊕ , ⊙ ) : Σ X . ( Σ y . Π z . ϕ ( X , z )) ⊕ ( Π z 1 . Π z 2 . θ ( X , z 1 , z 2 )) QMSO ( Σ x Π 1 x , ⊕ , ⊙ ) : Σ x . ( Σ y . Π z . ϕ ( x , y , z )) ⊙ ( Π z . θ ( x , z )) QMSO ( Π n x , ⊕ , ⊙ ) , n ∈ N : Π x 1 . ⋯ Π x n . θ ( x 1 , . . . , x n )

  15. QMSO and weighted automata QMSO is too expressive to capture weighted automata! Over ( N , + , ⋅ , 0 , 1 ) ⟦ Π x . Π y . 2 ⟧( w ) = 2 ∣ w ∣ 2 . For every weighted automata A over ( N , + , ⋅ , 0 , 1 ) : ⟦A⟧( w ) ∈ 2 O (∣ w ∣)

  16. QMSO and weighted automata QMSO is too expressive to capture weighted automata! Definition Quantitative Iteration Logic (QIL) ∶ = QMSO ( Σ X , x Π 1 x , ⊕ , ⊙ ) . Theorem A function f ∶ Γ ∗ → S is definable by a weighted automaton over S and Γ if, and only if, f is definable by a formula in QIL [ S , Γ ] . Weighted Automata ≡ QIL .

  17. Undecidable properties of QIL Quantitative generalization of classical decision problems: Equivalence: ⟦ θ 1 ⟧( w ) = ⟦ θ 2 ⟧( w ) for all w ∈ Γ ∗ , Containment: ⟦ θ 1 ⟧( w ) ≤ ⟦ θ 2 ⟧( w ) for all w ∈ Γ ∗ . Proposition The following problems are undecidable: 1. Containment of formulas in QMSO ( Σ x Π 1 x , ⊕ , ⊙ ) over ( N , + , ⋅ , 0 , 1 ) . 2. Equivalence and containment of formulas in QMSO ( Σ x Π 1 x , ⊕ , ⊙ ) over ( N ∞ , min , + , ∞ , 0 ) .

  18. Outline QMSO and WA QMSO and subclasses of WA Beyond WA Conclusions

  19. Different fragments of QMSO captures different subclasses of WA Classes of Weighted Automata (WA) depending on the ambiguity: Deterministic WA (DWA). Unambiguous WA ( unamb - WA): ∣ Run A ( w )∣ ≤ 1 for all w ∈ Σ ∗ Finite Ambiguous WA ( fin - WA): ∣ Run A ( w )∣ < k for all w ∈ Σ ∗ Polynomially Ambiguous WA ( poly - WA): ∣ Run A ( w )∣ ∈ O (∣ w ∣ k ) DWA ⊊ unamb - WA ⊊ fin - WA ⊊ poly - WA ⊊ WA

  20. Unambiguous and finitely ambiguous weighted automata are captured by QMSO Subfragment QMSO ( Op , ⊕ b ) : ⊕ -operator is restricted to a “ base ” level. Example ( Π x . P a ( x ) ⊕ P b ( x )) ⊙ ( Π x . ∃ z . x ≤ z ∧ P a ( z )) QMSO ( Π 1 x , ⊕ b , ⊙ ) ∈ ( Π x . P a ( x ) ⊕ P b ( x )) ⊕ ( Π x . ∃ z . x ≤ z ∧ P a ( z )) QMSO ( Π 1 x , ⊕ b , ⊙ ) ∉

  21. Unambiguous and finitely ambiguous weighted automata are captured by QMSO Subfragment QMSO ( Op , ⊕ b ) : ⊕ -operator is restricted to a “ base ” level. Theorem ≡ QMSO ( Π 1 x , ⊕ b , ⊙ ) unamb - WA ≡ QMSO ( Π 1 x , ⊕ , ⊙ ) fin - WA Proof idea. From QMSO ( Π 1 x , ⊕ b , ⊙ ) to unamb - WA: Exploit unambiguity to express formulas of the form Π x . ⊕ ⊙ ϕ i , j ( x ) . i ∈ I j ∈ J From QMSO ( Π 1 x , ⊕ , ⊙ ) to fin - WA: Use disambiguation theorem presented in Klimann et all, 2004.

  22. Polynomial ambiguous weighted automata are also captured by QMSO Theorem poly - WA ≡ QMSO ( Σ x Π 1 x , ⊕ , ⊙ ) Proof idea. From poly - WA to QMSO ( Σ x Π 1 x , ⊕ , ⊙ ) : Exploit structural properties of the components of a poly - WA.

  23. Which fragment captures deterministic weighted automata? The forward-iterator ( ⋅ ) → and the backward-iterator ( ⋅ ) ← n ⟦ θ → ⟧( w , σ ) ⟦ θ ⟧( w [ 1 .. i ] , σ ) = ⊙ i = 1 n ⟦ θ ← ⟧( w , σ ) ⟦ θ ⟧( w [ i .. n ] , σ ) = ⊙ i = 1 Over ( N ∞ , min , + , ∞ , 0 ) f ( w ) = number of prefixes of w that satisfy ϕ . ( min { ϕ + 1 , ¬ ϕ }) → .

Recommend

More recommend