CSCI 3210: Computational Game Theory Inefficiency of Equilibria - PDF document

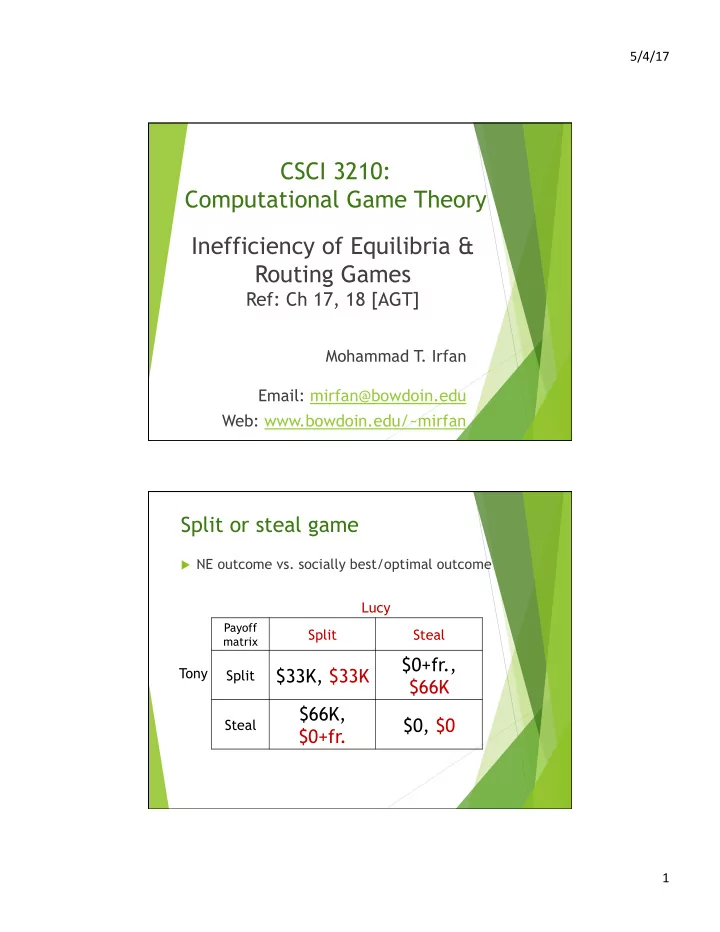
5/4/17 CSCI 3210: Computational Game Theory Inefficiency of Equilibria & Routing Games Ref: Ch 17, 18 [AGT] Mohammad T . Irfan Email: mirfan@bowdoin.edu Web: www.bowdoin.edu/~mirfan Split or steal game u NE outcome vs. socially best/optimal outcome Lucy Payoff Split Steal matrix $0+fr., Tony $33K, $33K Split $66K $66K, $0, $0 Steal $0+fr. 1

5/4/17 Prisoner's "dilemma" game u Again: NE outcome vs socially optimal outcome Suspect 2 Payoff Not Confess Confess matrix Not 1, 1 10, 0 Suspect 1 Confess 0, 10 5, 5 Confess Costs (negative of payoffs) Measuring the inefficiency of NE u What is the objective function to compare different outcomes? u Utilitarian u Egalitarian u How to deal with multiplicity of NE? u Inefficiency of which NE? u Price of anarchy vs. price of stability 2

5/4/17 Price of Anarchy (PoA) u PoA = Worst objective function value of a NE Objective function value of optimal outcome Price of Stability (PoS) u PoS = Best objective function value of a NE Objective function value of optimal outcome 3

5/4/17 Example u Calculate PoA and PoS Suspect 2 Payoff Not Confess Confess matrix Not 1, 1 10, 0 Suspect 1 Confess 0, 10 5, 5 Confess Costs (negative of payoffs) Example u Calculate PoA and PoS Column player Payoff L R matrix 21, -1 10, 0 U Row player 100, 10 7, 8 D Costs (negative of payoffs) 4

5/4/17 PoA vs. PoS u Consider costs u PoA and PoS will be >= 1 u PoA = PoS when all NE have the same cost (e.g., unique NE) u In general, PoA >= PoS u PoA: worst case guarantee in a system of independent agents u PoS: measures benefit of a protocol or proposed outcome Pigou's example u Assume one unit of traffic from s to t u Objective function: average travel time x = amount of traffic on edge u NE: all traffic in lower edge. Avg cost = 1. u Optimal: ½ and ½ . Avg cost = ½ * 1 + ½ * ½ . u PoA, PoS = ? 5

5/4/17 Routing Games Model: nonatomic selfish routing u Multicommodity flow network u Directed network with multiple (source, sink) pairs u Each (source, sink) pair is called a commodity u r i amount of traffic for each commodity i u Each edge e has a delay or cost function c e u Every car going through an edge gets same delay u Cost of a path = sum of edge costs u Note: cost doesn't depend on identity of players u Congestion games 6

5/4/17 Equilibrium flow u Let f be a feasible flow (combining all commodities) u f is equilibrium flow if u A commodity uses a path P in its flow within f => All detours have higher (or equal) delay equilibrium flow More complex graphs t 1 s 1 s 2 t 2 u What is the traffic flow on an (s,t) path? u Amount of traffic using that path fully (not partially) to go from s à t u What's the cost (or delay) of a path? u Total delay on that path – traffic using part of that path also contribute to delay 7

5/4/17 Cost of an (s,t) path u Sum of edge costs (or delays) on that path flow on edge e cost function path flow of edge e (all the flows, not just on P) Cost of a flow u Cost (or delay) of a flow = sum of (cost of each path * flow on that path) = sum of (cost of each edge * flow on that edge) flow on edge e flow cost function of edge e 8

5/4/17 Example: nonlinear Pigou u Consider large number p; 1 unit of traffic equilibrium flow u Equilibrium: All down. cost = 1. u Optimal: ε up, (1- ε ) down PoA à + ∞ u Cost = ε * 1 + (1- ε ) * (1- ε ) p à 0 Example: Braess' paradox u 1 unit of traffic ½ equilibrium flow ½ PoA = 1 Equilibrium cost = ½ * ( ½ + 1) + ½ * (1 + ½ ) =3/2 9

5/4/17 Braess' paradox u New super highway between v and w PoA = 4/3 • Equilibrium cost = 1 + 1 = 2 • Optimal: ½ and ½ (ignore superhighway) Another model: atomic selfish routing u Restricted version of multicommodity flow u r i amount of traffic for each commodity i u Each s à t flow must go through a single path (difference with nonatomic selfish routing) u Each player/commodity chooses the minimum delay path w.r.t. others' choices u Equilibrium flow: No better path for any player 10

5/4/17 Drawback of the atomic model u There may not exist any equilibrium flow u 2 players: both s à t u r 1 = 1, r 2 = 2 u Proof: If player 2 goes s à t, then player 1's BR is s à v à w à t, to which player 2's BR is s à w à t. (and so on) Nonatomic model: equilibrium existence u Prove that equilibrium flow exists 11

5/4/17 Price of anarchy: nonatomic u Consider linear cost functions only u Pigou's example gives a lower bound of 4/3 x = amount of traffic on edge u NE: all traffic in lower edge. Avg cost = 1. u Optimal: ½ and ½ . Avg cost = ½ * 1 + ½ * ½ = 3/4. u PoA = 1 / (3/4) = 4/3 Surprise! u Price of anarchy for any nonatomic routing game with linear costs <= 4/3 12