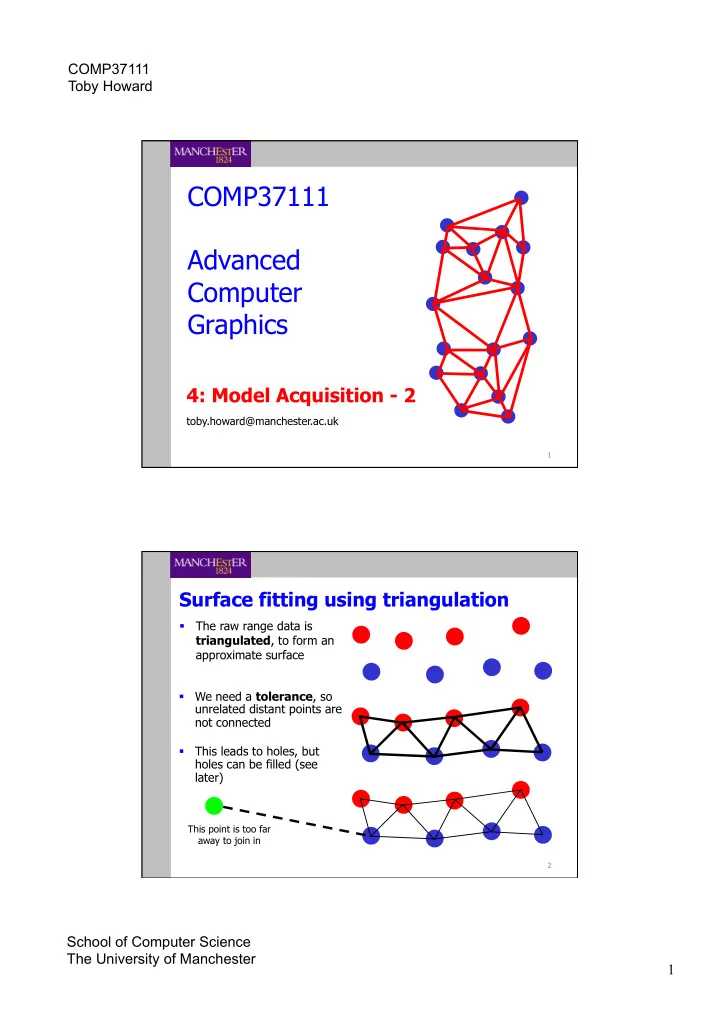
COMP37111 Advanced Computer Graphics 4: Model Acquisition - 2 - PDF document

COMP37111 Toby Howard COMP37111 Advanced Computer Graphics 4: Model Acquisition - 2 toby.howard@manchester.ac.uk 1 Surface fitting using triangulation § The raw range data is triangulated , to form an approximate surface § We need a tolerance , so unrelated distant points are not connected § This leads to holes, but holes can be filled (see later) This point is too far away to join in 2 School of Computer Science The University of Manchester 1

COMP37111 Toby Howard How to triangulate? § We can guess a simple algorithm to triangulate this: § But what about this point set (more likely): 3 Example point set 4 School of Computer Science The University of Manchester 2

COMP37111 Toby Howard Example point set 0.001565 26.307560 151.121063 91.730026 106.553444 43.791836 9.408923 135.772949 135.859283 186.938583 76.700417 103.883278 166.193069 6.914422 10.692327 105.940041 134.229874 1.539637 76.683128 13.368447 83.497200 137.354538 117.795326 186.087296 169.233383 105.385757 18.392979 130.783798 83.199867 140.238113 182.064163 152.439606 52.490597 9.492903 147.216385 65.646843 126.527718 151.282089 198.207474 73.067734 49.407776 196.510056 144.532089 150.671173 130.303711 14.537176 126.326942 176.941437 54.541992 87.282280 153.298950 95.546356 47.554886 54.981369 71.852997 33.301441 97.303474 179.531250 181.841629 12.112865 180.930618 100.904587 103.258392 63.806587 197.328430 98.795334 53.228905 18.146580 189.552856 14.749815 100.141418 76.828430 55.416359 182.763489 105.949471 92.889168 188.195984 10.016797 152.302856 154.040909 165.563461 25.073074 3.173540 137.691055 173.649429 125.908684 147.244904 145.082397 199.891586 177.714447 46.638973 61.264366 70.203049 102.654739 118.222717 169.196304 82.416153 168.302124 53.863453 5 83.078918 107.460800 93.583473 A triangulation algorithm Convex hull 6 School of Computer Science The University of Manchester 3

COMP37111 Toby Howard Examples of triangulations 7 Triangulation § This is a hard problem § Many possible solutions for a given set § What makes a particular solution “desirable” ? § Regularity: roughly similar-sized triangles § No “degenerate” triangles ( v1==v2 (==v3) ) § Speed of algorithm (time/space complexity) 8 School of Computer Science The University of Manchester 4

COMP37111 Toby Howard Delaunay Triangulation § Invented by Boris Delaunay in 1934 § A special kind of triangulation… § …with some useful properties 9 Delaunay Triangulation properties § The boundary of the triangulation is the convex hull of the points § The circumcircle of each triangle overlaps no other triangles § Triangles have the largest possible interior angles (so long, thin, triangles are rare) § A Deluanay triangulation of a point set P is a triangulation where every edge E is a “Delaunay edge” 10 School of Computer Science The University of Manchester 5

COMP37111 Toby Howard Delauney edges Examples of § Given a set of points P possible circles though P 1 P 2 § An edge P 1 P 2 is a “Delaunay edge”… P 1 P 2 § …IFF it is possible to draw a circle through P 1 P 2 such that the circle contains no other vertices from P 11 Let’s look a Delaunay edge at a few edges… A B a Delaunay edge NOT a Delaunay edge: it’s impossible to draw a circle passing through edge AB which doesn’t enclose any other vertices 12 School of Computer Science The University of Manchester 6

COMP37111 Toby Howard Delaunay triangle § Following the definition of a Delaunay edge, a triangle T is called a Delaunay triangle IFF its circumcircle does not enclose any other vertices in P T 1 T 2 § T 1 is not a Delaunay triangle. But T 2 is. 13 Delaunay Triangle algorithm Create a big dummy triangle that surrounds the § T 1 entire point set. Mark all P i as “not done”. Then: T 2 T 3 1. Choose a random “not done” point P i , and T find a triangle T which encloses it. 2. Split T into smaller triangles T 1 ,T 2 ,T 3 with P i as a vertex. 3. For each triangle, check its circumcircle to see if it is Delaunay. If it is, OK. If it isn’t, swap edges around (the fiddly bit, details ignored) until it is. T 1 4. Mark P i “done”. P i T 2 T 3 5. Repeat from step 1 until all P i are “done”. T § Efficiency of algorithm is crucial for huge datasets 14 School of Computer Science The University of Manchester 7

COMP37111 Toby Howard Delaunay triangulation result … compared to some random triangulations: 15 Delaunay Triangulation applets § http://www.cs.cornell.edu/home/chew/Delaunay.html § Comparison of different algorithms: http://goanna.cs.rmit.edu.au/~gl/research/ comp_geom/delaunay/delaunay.html (excellent example of algorithms with different complexities) § http://www.cse.unsw.edu.au/~lambert/java/3d/ delaunay.html 16 School of Computer Science The University of Manchester 8

COMP37111 Toby Howard Laser scanning Raw range data 17 Laser scanning Triangulated range data 18 School of Computer Science The University of Manchester 9

COMP37111 Toby Howard Mesh simplification § In many cases we have too much data § Space complexity § Time complexity § Difficult to render in real-time § So we simplify the mesh by removing vertices, but preserving shape § Many methods have been developed, still ongoing field of research § The following example uses “Quadratic Edge Collapse” – see “Surface Simplification Using Quadratic Error Metrics, http://www1.cs.columbia.edu/~cs4162/html05s/garland97.pdf (the paper itself is not examinable). 19 Simplification by edge collapse § We collapse edges between P1 and P2 into a single point and adjust triangulation § We select candidate points based on an estimation of error – for example || P2-P1 ||, but many different approaches used to quantify error P2 P1 20 School of Computer Science The University of Manchester 10

COMP37111 Toby Howard Simplification by edge collapse § P1 and P2 are removed and replaced by their mid-point M § The two green triangles will be removed § Edges which previously connected to P1 or P2 will be moved to M (and duplicates removed) M P2 P1 21 Simplification by edge collapse § The resulting mesh retains its convex hull § Changes are localised within the mesh § The key to the success of the method is the computation of a suitable error metric for vertices, for choosing which to collapse M 22 School of Computer Science The University of Manchester 11

COMP37111 Toby Howard FOR YOU TO DO Example of Simplification These simplification Triangles = 25000 examples were produced using Meshlab (meshlab.sourceforge.net) Download it and try some simplification experiments with its sample objects 23 Example of Simplification Triangles = 12000 24 School of Computer Science The University of Manchester 12

COMP37111 Toby Howard Example of Simplification Triangles = 6000 25 Example of Simplification Triangles = 3000 26 School of Computer Science The University of Manchester 13

COMP37111 Toby Howard Example of Simplification Triangles = 500 27 Surface fitting Raw range data Approximated surface 28 School of Computer Science The University of Manchester 14

COMP37111 Toby Howard Integration of texture www.impactstudiostv.com 29 Integration of texture http://www.impactstudiostv.com 30 School of Computer Science The University of Manchester 15

COMP37111 Toby Howard Solving the occlusion problem § Left: photograph of model § Right: reconstruction: graphics.stanford.edu/papers/volrange/ occlusions lead to sparse range data 31 Solving the occlusion problem § Most models self-occlude… § … so no single range image can capture a model § Parts of the captured model will be missing § We need to take multiple range images and combine them… how? § Basic approach: § Sets of range data are registered § Data is filtered § Attempt to estimate a new “ideal” surface that is “closest” to as many range points as possible § Remesh “ideal” surface into triangles § Paper: “ Zippered Polygon Meshes from Range Images ” (required reading, examinable) 32 School of Computer Science The University of Manchester 16

COMP37111 Toby Howard Case Study: Digital Michelangelo Project § Stanford University, from 1999 and ongoing graphics.stanford.edu/projects/mich/ § Scan depth resolution = 0.1mm § Scan sample resolution = 0.29mm 33 34 School of Computer Science The University of Manchester 17

COMP37111 Toby Howard Remote rendering of large data sets ScanView: graphics.stanford.edu/software/scanview FOR YOU TO DO : download Scanview and try it 35 Scanview: remote rendering of large data sets internet Secure server Client Server returns high-res rendering as a texture Local interaction Client requests Computes with free high-res rendering, high-res low-res model sending parameters rendering on demand internet 36 School of Computer Science The University of Manchester 18

COMP37111 Toby Howard Filling in holes § A different method for dealing with holes caused by occlusions is “volumetric diffusion” § http://graphics.stanford.edu/papers/holefill-3dpvt02 37 Acquired model: 1mm Photograph of original resolution, 4m polygons 38 School of Computer Science The University of Manchester 19