Applications of Renormalization Group Methods in Nuclear Physics 3 - PowerPoint PPT Presentation

Applications of Renormalization Group Methods in Nuclear Physics – 3 Dick Furnstahl Department of Physics Ohio State University HUGS 2014

Outline: Lecture 3 Lecture 3: Effective field theory Recap from lecture 2: How SRG works Motivation for nuclear effective field theory Chiral effective field theory Universal potentials from RG evolution Extra: Quantitative measure of perturbativeness

Outline: Lecture 3 Lecture 3: Effective field theory Recap from lecture 2: How SRG works Motivation for nuclear effective field theory Chiral effective field theory Universal potentials from RG evolution Extra: Quantitative measure of perturbativeness

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Flow equations in action: NN only In each partial wave with ǫ k = � 2 k 2 / M and λ 2 = 1 / √ s dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ ) + ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q

Basics: SRG flow equations [e.g., see arXiv:1203.1779] Transform an initial hamiltonian, H = T + V , with U s : H s = U s HU † s ≡ T + V s , where s is the flow parameter . Differentiating wrt s : dH s η s ≡ dU s ds U † s = − η † ds = [ η s , H s ] with s . η s is specified by the commutator with Hermitian G s : η s = [ G s , H s ] , which yields the unitary flow equation ( T held fixed), dH s ds = dV s ds = [[ G s , H s ] , H s ] . Very simple to implement as matrix equation (e.g., MATLAB) G s determines flow = ⇒ many choices ( T , H D , H BD , . . . )

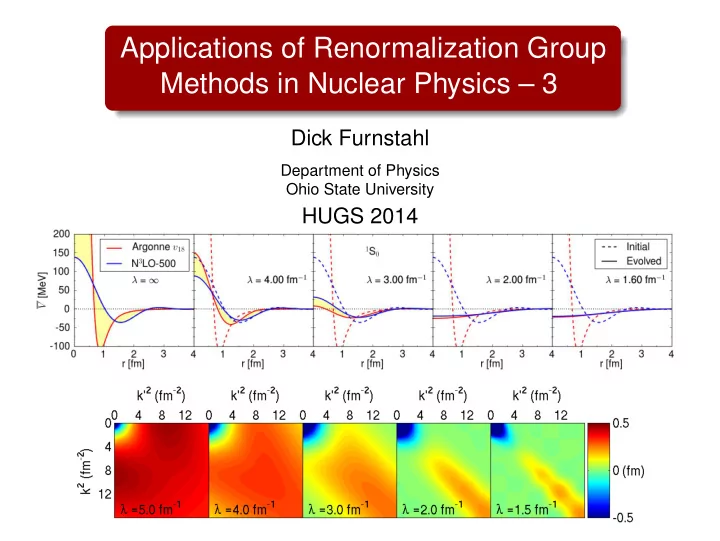
SRG flow of H = T + V in momentum basis → H s = U s HU † Takes H − s in small steps labeled by s or λ √ dH s ds = dV s λ 2 = 1 / ds = [[ T rel , V s ] , H s ] with T rel | k � = ǫ k | k � and s For NN, project on relative momentum states | k � , but generic dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ )+ ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q V λ = 3 . 0 ( k , k ′ ) V λ = 2 . 5 ( k , k ′ ) 1st term 2nd term First term drives 1 S 0 V λ toward diagonal: V λ ( k , k ′ ) = V λ = ∞ ( k , k ′ ) e − [( ǫ k − ǫ k ′ ) /λ 2 ] 2 + · · ·

SRG flow of H = T + V in momentum basis → H s = U s HU † Takes H − s in small steps labeled by s or λ √ dH s ds = dV s λ 2 = 1 / ds = [[ T rel , V s ] , H s ] with T rel | k � = ǫ k | k � and s For NN, project on relative momentum states | k � , but generic dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ )+ ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q V λ = 2 . 5 ( k , k ′ ) V λ = 2 . 0 ( k , k ′ ) 1st term 2nd term First term drives 1 S 0 V λ toward diagonal: V λ ( k , k ′ ) = V λ = ∞ ( k , k ′ ) e − [( ǫ k − ǫ k ′ ) /λ 2 ] 2 + · · ·

SRG flow of H = T + V in momentum basis → H s = U s HU † Takes H − s in small steps labeled by s or λ √ dH s ds = dV s λ 2 = 1 / ds = [[ T rel , V s ] , H s ] with T rel | k � = ǫ k | k � and s For NN, project on relative momentum states | k � , but generic dV λ � d λ ( k , k ′ ) ∝ − ( ǫ k − ǫ k ′ ) 2 V λ ( k , k ′ )+ ( ǫ k + ǫ k ′ − 2 ǫ q ) V λ ( k , q ) V λ ( q , k ′ ) q V λ = 2 . 0 ( k , k ′ ) V λ = 1 . 5 ( k , k ′ ) 1st term 2nd term First term drives 1 S 0 V λ toward diagonal: V λ ( k , k ′ ) = V λ = ∞ ( k , k ′ ) e − [( ǫ k − ǫ k ′ ) /λ 2 ] 2 + · · ·

Outline: Lecture 3 Lecture 3: Effective field theory Recap from lecture 2: How SRG works Motivation for nuclear effective field theory Chiral effective field theory Universal potentials from RG evolution Extra: Quantitative measure of perturbativeness

“Traditional” nucleon-nucleon interaction (from T. Papenbrock)

Local nucleon-nucleon interaction for non-rel S-eqn Depends on spins and isospins of nucleons; non-central longest-range part is one-pion-exchange potential � e − m π r � 3 3 ( 3 σ 1 · ˆ r σ 2 · ˆ V π ( r ) ∝ ( τ 1 · τ 2 ) r − σ 1 · σ 2 )( 1 + m π r + ( m π r ) 2 ) + σ 1 · σ 2 r Characterize operator structure of shorter-range potential central, spin-spin, non-central tensor and spin-orbit { 1 , σ 1 · σ 2 , S 12 , L · S , L 2 , L 2 σ 1 · σ 2 , ( L · S ) 2 } ⊗ { 1 , τ 1 · τ 2 } 200 S=1, T=0 deuteron proton-neutron 100 L = 0 relative state V(r) (MeV) S=0,T=1 Tensor = ⇒ deuteron wf is 0 mixed S ( L = 0) and D ( L = 2) Argonne v18 -100 Non-zero The quantum numbers of the deuteron -200 quadrupole have the deepest potential well! moment -300 0 1 2 3 4 5 6 r (fm)

Problems with Phenomenological Potentials The best potential models can describe with χ 2 / dof ≈ 1 all of the NN data (about 6000 points) below the pion production threshold. So what more do we need? Some drawbacks: Usually have very strong repulsive short-range part = ⇒ requires special (non-systematic) treatment in many-body calculations (e.g. nuclear structure). Difficult to estimate theoretical errors and range of applicability. Three-nucleon forces (3NF) are largely unconstrained and unsystematic models. How to define consistent 3NF’s and operators (e.g., meson exchange currents)? Models are largely unconnected to QCD (e.g., chiral symmetry). Don’t connect NN and other strongly interacting processes (e.g., ππ and π N ). Lattice QCD will be able to predict NN, 3N observables for high pion masses. How to extrapolate to physical pion masses? Alternative: Use Chiral Effective Field Theory (EFT)

QCD and Nuclear Forces Quarks and gluons are the fundamental QCD dof’s, but . . . At low energies (low resolution), use “collective” degrees of freedom = ⇒ (colorless) hadrons. Which ones?

Different EFTs depending on scale of interest LQCD scale& separa)on& constituent quarks ab initio Resolution CI DFT collective models