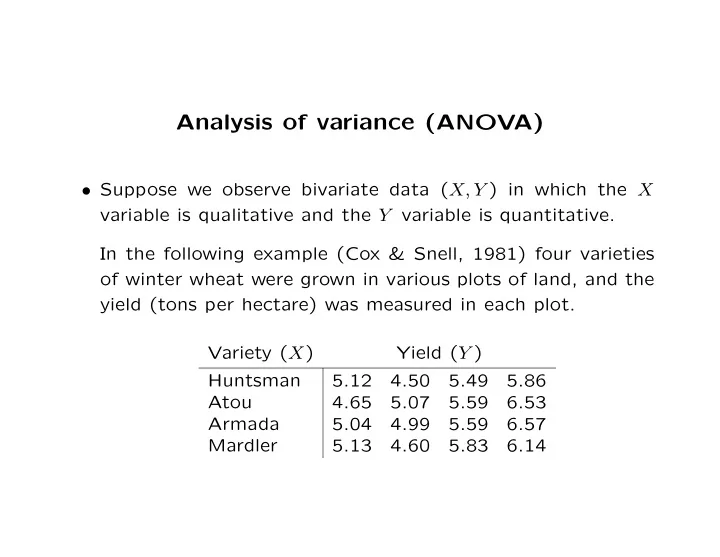

Analysis of variance (ANOVA) • Suppose we observe bivariate data ( X, Y ) in which the X variable is qualitative and the Y variable is quantitative. In the following example (Cox & Snell, 1981) four varieties of winter wheat were grown in various plots of land, and the yield (tons per hectare) was measured in each plot. Variety ( X ) Yield ( Y ) Huntsman 5.12 4.50 5.49 5.86 Atou 4.65 5.07 5.59 6.53 Armada 5.04 4.99 5.59 6.57 Mardler 5.13 4.60 5.83 6.14
The X variable is the type of wheat, which is qualitative, and in this context is called a factor. Specifically, it is a four level factor, since there are four types of wheat. In general, we will use m to denote the number of levels of the factor. All 16 data values are assumed to be independent. The four values in a given row are independent and identically distributed (iid), and are referred to as replicates. Note that this implies a key assumption – it is assumed that the mean and variance within each row are fixed. Our primary interest will be whether the means for different rows (different varieties of wheat) differ. This would imply that some varieties of wheat are better than others. The analysis is easiest when we assume that the variances for all rows are the same.
This type of data is called a balanced one-way layout. The term “balance” refers to the fact that there are the same number of observations in every row. The term “one-way” refers to the fact that there is only one X variable. • Our notation for this type of data will be Y ij , where i = 1 , 2 , 3 , 4 indicates the type of wheat (i.e. 1 = Huntsman, 2 = Atou, 3 = Armada, 4 = Mardler), and j indexes the replicates. Thus, Y 11 = 5 . 12, Y 12 = 4 . 50, Y 21 = 4 . 65, Y 44 = 6 . 14, etc. Additional notation: Y i · = � j Y ij is the sum of all values in the i th row, n is the number of values in each row (4 in the example above), ¯ Y i · = Y i · /n is the average value in the i th row, Y ·· = � ij Y ij is the sum of all observations, and ¯ Y ·· = Y ·· /mn is the overall (“grand”) mean.
All of these values can be displayed in an ANOVA table: ¯ Variety ( X ) Yield ( Y ) Y i · Y i · Huntsman 5.12 4.50 5.49 5.86 20.97 5.24 Atou 4.65 5.07 5.59 6.53 21.84 5.46 Armada 5.04 4.99 5.59 6.57 22.19 5.55 Mardler 5.13 4.60 5.83 6.14 21.70 5.43 86.7 5.42 where the values in the lower right are Y ·· = 86 . 7 and ¯ Y ·· = 5 . 42. • Analysis of variance (ANOVA) specifies the following simple model for these data:
Y ij = µ + α i + ǫ ij . The constant values µ, α 1 , α 2 , α 3 , and α 4 are unknown pa- rameters of the population, and the random variables ǫ ij are iid errors with mean 0 and a common unknown variance σ 2 . For example, the model gives the following for certain specific data points: = µ + α 1 + ǫ 11 Y 11 = µ + α 1 + ǫ 14 Y 14 Y 23 = µ + α 2 + ǫ 23 Y 42 = µ + α 4 + ǫ 42 .
• One difficulty with the above model is that different values of µ and the α i will give the same mean values for every data point. Specifically, if we replace µ with µ + c and replace each α i with α i − c , the means will not change. When this occurs the parameters are said to be unidentified. To estimate the parameters, we must impose a constraint. In the present situation, the constraint will be � i α i = 0. This allows the α i to be interpreted as “deviations from the mean” – if α 2 = 3, then Atou wheat yields on average three tons more than the overall mean, and if α 4 = − 2, Mardler wheat yields on average two tons less than the overall mean. • In order to estimate the population parameters, we use the same “sum of squared residuals” function that was used for simple linear regression:
α i ) 2 . � ( Y ij − ˆ µ − ˆ ij As with simple linear regression, our estimates will be the val- ues that we get by searching for the values of ˆ µ , ˆ α 1 , . . . , ˆ α 4 that make the sum of squared residuals as small as possi- ble. Without derivation, the following are the least squares parameter estimates: Y i · − ¯ ¯ ˆ = α i Y ·· ¯ ˆ = µ Y ·· For the example given above we get
α 1 ˆ = − 0 . 176 ˆ = 0 . 041 α 2 ˆ = 0 . 129 α 3 ˆ = 0 . 006 α 4 ˆ µ = 5 . 42 Also by analogy with simple linear regression, we can define fitted values ˆ Y ij = ˆ µ + ˆ α i residuals
r ij = Y ij − ˆ µ − ˆ α i , and an estimate of the standard deviation �� r 2 ˆ σ = ij / ( mn − m ) . i • Since EY i 1 = · · · = EY in = µ + α i , it follows that E ¯ Y i · = µ + α i . Similarly, E ¯ Y ·· = µ + � i α i /m = µ . Thus E ˆ α i = µ + α i − µ = α i , so ˆ α i is unbiased. Similarly it can be shown that ˆ µ is unbiased.
• The variance of each ˆ α i can be calculated directly: var(¯ Y i · − ¯ var(ˆ α i ) = Y ·· ) var(¯ Y i · ) + var(¯ Y ·· ) − 2cov(¯ Y i · , ¯ = Y ·· ) σ 2 /n + σ 2 /mn − 2cov( Y i · , Y ·· ) /n 2 m = σ 2 /n + σ 2 /mn − 2cov( Y i · , Y i · ) /n 2 m = σ 2 /n + σ 2 /mn − 2 nσ 2 /n 2 m = σ 2 /n + σ 2 /mn − 2 σ 2 /mn = σ 2 /n − σ 2 /mn = σ 2 · m − 1 = mn .
• Based on the variance formula for ˆ α i , we can carry out hy- pothesis tests. For example, to test α 2 = 0 versus α 2 > 0, the test statistic would be � mn T = ˆ α 2 σ · m − 1 . ˆ When α 2 = 0 (the null hypothesis) T has a t m ( n − 1) distribu- tion. In ANOVA problems it is common for m ( n − 1) to be small, so the normal approximation should not generally be used. In the above example, we get ˆ σ = . 71, so the (two sided) test statistics and p-values are as follows:
Parameter Estimate | T | p-value α 1 -0.176 0.57 .58 α 2 0.041 0.13 .90 0.129 0.42 .68 α 3 0.006 0.02 .98 α 4 So in the example, none of the coefficients are significantly different from zero – we can not confidently conclude that any variety of wheat is better than the others. As we have seen previously, the test statistic − T can be used to test the alternative hypothesis α 2 < 0, and the test statistic | T | can be used to test the alternative hypothesis α 2 � = 0. • We can also use the standard deviation formula to get a CI for any of the α i ’s. Since
� mn � � Q ( . 025) ≤ ˆ α 2 − α 2 P · m − 1 ≤ Q ( . 975) = . 95 , σ ˆ where Q is the t m ( n − 1) quantile function, it follows that � � m − 1 m − 1 = . 95 . P ˆ α 2 − ˆ σQ ( . 975) ≤ α 2 ≤ ˆ α 2 + ˆ σQ ( . 975) mn mn The confidence intervals for the example are: α 1 ( − . 84 , . 48) α 2 ( − . 62 , . 70) α 3 ( − . 53 , . 79) α 4 ( − . 65 , . 67).
• As with simple linear regression, we have a “sum of squares law”: SSTO = SSE + SSR Y ij ) 2 + Y ·· ) 2 Y ·· ) 2 , ( Y ij − ¯ ( Y ij − ˆ (ˆ Y ij − ¯ � � � = ij ij ij where SSR and SSE are uncorrelated. We can define “mean squares”: Sum of Squares DF Mean square SSTO mn-1 SSTO / (mn-1) SSR m-1 SSR / (m-1) SSE m(n-1) SSE / (m(n-1))
Large values of SSR and small values of SSE suggest a good fit to the model. Therefore F = MSR/MSE can be used to test the fit of the model. F has a F distribution with ( m − 1 , m ( n − 1)) degrees of freedom. In the example, the sums of squares are SSTO= 6 . 2350, SSR= 0 . 1975, and SSE= 6 . 0374. The mean squares are MSTO= 0 . 5196, MSR= 0 . 0658, and MSE= 0 . 5031. The F statistic is F = . 13079, which gives an insignficant p-value of around . 94. Thus there is no evidence that any type of wheat has greater or lesser yield than any other.
Unabalanced one-way layout • The balanced one way layout can easily be generalized to the unbalanced case, where differing numbers of replicates are made for different factor levels. In this case, we use n i to denote the number of replicates for factor level i , and let N = � i n i denote the total number of observations. The definitions of Y i · and Y ·· are the same as in the balanced case, but now we have ¯ Y i · = Y i · /n i and ¯ Y ·· = Y ·· /N . µ , ˆ The definitions of ˆ α i , ˆ Y ij , and r ij are the same as in the balanced case.
In the unbalanced one-way ANOVA, the α i are identified by requiring � n i α i = 0 . i The standard deviation estimate becomes: �� r 2 ˆ σ = ij / ( N − m ) . ij The variance of ˆ α i becomes: α i ) = σ 2 (1 /n i − 1 /N ) = σ 2 N − n i Var(ˆ . Nn i
The test statistic for a hypothesis test α i = 0 versus α i > 0 is � Nn i T = ˆ α i / ˆ σ, N − n i which has a t N − m distribution. Since � � � Q ( . 025) ≤ ˆ α i − α i Nn i ≤ Q ( . 975) = . 95 , P · ˆ σ N − n i where Q is the t N − m quantile function, it follows that
� � � � N − n i N − n i P α i − ˆ ˆ σQ ( . 975) ≤ α i ≤ ˆ α i + ˆ σQ ( . 975) = . 95 . Nn i Nn i • The sum of squares law is the same as in the balanced case, however the degrees of freedom must be generalized: Sum of Squares DF Mean square SSTO N-1 SSTO / (N-1) SSR m-1 SSR / (m-1) SSE N-m SSE / (N-m) Note that for everything above, the formulas for the balanced case are special cases of the formulas for the unbalanced case, replacing n i with n , and nm with N .
Recommend
More recommend