13. Graphs Notation, Representation, Graph Traversal (DFS, BFS), - PowerPoint PPT Presentation

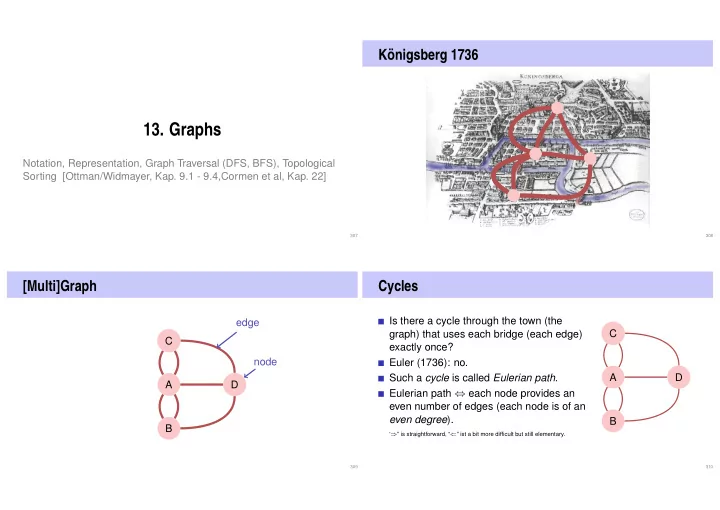
K¨ onigsberg 1736 13. Graphs Notation, Representation, Graph Traversal (DFS, BFS), Topological Sorting [Ottman/Widmayer, Kap. 9.1 - 9.4,Cormen et al, Kap. 22] 307 308 [Multi]Graph Cycles Is there a cycle through the town (the edge graph) that uses each bridge (each edge) C C exactly once? node Euler (1736): no. Such a cycle is called Eulerian path . A D A D Eulerian path ⇔ each node provides an even number of edges (each node is of an even degree ). B B ‘ ⇒ ” is straightforward, “ ⇐ ” ist a bit more difficult but still elementary. 309 310

Notation Notation 1 1 A directed graph consists of a set V = { v 1 , . . . , v n } of nodes ( Vertices) and a set E ⊆ V × V of Edges. The same edges may not be contained more than once. 2 3 2 3 1 2 4 5 4 5 undirected directed 5 3 4 V = { 1 , 2 , 3 , 4 , 5 } V = { 1 , 2 , 3 , 4 , 5 } loop E = {{ 1 , 2 } , { 1 , 3 } , { 2 , 3 } , { 2 , 4 } , E = { (1 , 3) , (2 , 1) , (2 , 5) , (3 , 2) , { 2 , 5 } , { 3 , 4 } , { 3 , 5 } , { 4 , 5 }} (3 , 4) , (4 , 2) , (4 , 5) , (5 , 3) } 311 312 Notation Notation An undirected graph consists of a set V = { v 1 , . . . , v n } of nodes a An undirected graph G = ( V, E ) without loops where E comprises and a set E ⊆ {{ u, v }| u, v ∈ V } of edges. Edges may bot be all edges between pairwise different nodes is called complete . contained more than once. 22 1 1 5 2 5 2 3 4 3 4 a complete undirected graph undirected graph 22 As opposed to the introductory example – it is then called multi-graph. 313 314

Notation Notation A weighted graph G = ( V, E, c ) is a graph G = ( V, E ) with an edge A graph where V can be partitioned into disjoint sets U and W such weight function c : E → ❘ . c ( e ) is called weight of the edge e . that each e ∈ E provides a node in U and a node in W is called bipartite . 2 5 1 1 4 4 4 2 3 1.5 0 3 315 316 Notation Notation For directed graphs G = ( V, E ) For directed graphs G = ( V, E ) w ∈ V is called adjacent to v ∈ V , if ( v, w ) ∈ E Predecessors of v ∈ V : N − ( v ) := { u ∈ V | ( u, v ) ∈ E } . In-Degree : deg − ( v ) = | N − ( v ) | , Successors : N + ( v ) := { u ∈ V | ( v, u ) ∈ E } Out-Degree : deg + ( v ) = | N + ( v ) | p 3 s 2 p 2 v w v deg − ( v ) = 3 , deg + ( v ) = 2 deg − ( w ) = 1 , deg + ( w ) = 1 s 1 p 1 N + ( v ) N − ( v ) 317 318

Notation Relationship between node degrees and number of edges For undirected graphs G = ( V, E ) : w ∈ V is called adjacent to v ∈ V , if { v, w } ∈ E Neighbourhood of v ∈ V : N ( v ) = { w ∈ V |{ v, w } ∈ E } For each graph G = ( V, E ) it holds Degree of v : deg( v ) = | N ( v ) | with a special case for the loops: 1 � v ∈ V deg − ( v ) = � increase the degree by 2 . v ∈ V deg + ( v ) = | E | , for G directed 2 � v ∈ V deg( v ) = 2 | E | , for G undirected. v w deg( v ) = 5 deg( w ) = 2 319 320 Paths Connectedness Path : a sequence of nodes � v 1 , . . . , v k +1 � such that for each An undirected graph is called connected , if for eacheach pair i ∈ { 1 . . . k } there is an edge from v i to v i +1 . v, w ∈ V there is a connecting path. Length of a path: number of contained edges k . A directed graph is called strongly connected , if for each pair Weight of a path (in weighted graphs): � k v, w ∈ V there is a connecting path. i =1 c (( v i , v i +1 )) (bzw. � k i =1 c ( { v i , v i +1 } ) ) A directed graph is called weakly connected , if the corresponding undirected graph is connected. Simple path : path without repeating vertices 321 322

Simple Observations Cycles Cycle : path � v 1 , . . . , v k +1 � with v 1 = v k +1 generally: 0 ≤ | E | ∈ O ( | V | 2 ) Simple cycle : Cycle with pairwise different v 1 , . . . , v k , that does connected graph: | E | ∈ Ω( | V | ) not use an edge more than once. complete graph: | E | = | V |· ( | V |− 1) (undirected) Acyclic : graph without any cycles. 2 Maximally | E | = | V | 2 (directed ), | E | = | V |· ( | V | +1) (undirected) Conclusion: undirected graphs cannot contain cycles with length 2 2 (loops have length 1) 323 324 Representation using a Matrix Representation with a List Many graphs G = ( V, E ) with nodes Graph G = ( V, E ) with nodes v 1 . . . , v n stored as adjacency matrix 1 2 3 4 5 v 1 , . . . , v n provide much less than n 2 A G = ( a ij ) 1 ≤ i,j ≤ n with entries from { 0 , 1 } . a ij = 1 if and only if edge edges. Representation with adjacency from v i to v j . list : Array A [1] , . . . , A [ n ] , A i comprises a 2 2 3 linked list of nodes in N + ( v i ) .   1 2 0 1 1 1 0   1 2 0 0 0 0 0 3 4 5   3   0 1 0 1 1     3 0 0 0 0 0 5 4 5 4 0 0 1 0 1 5 4 Memory Consumption Θ( | V | + | E | ) . Memory consumption Θ( | V | 2 ) . A G is symmetric, if G undirected. 325 326

Runtimes of simple Operations Depth First Search Operation Matrix List Θ(deg + v ) Find neighbours/successors of v ∈ V Θ( n ) Θ( n 2 ) find v ∈ V without neighbour/successor Θ( n ) Θ(deg + v ) ( u, v ) ∈ E ? Θ(1) Θ(1) Θ(1) Insert edge Θ(deg + v ) Θ(1) Delete edge 327 328 Graph Traversal: Depth First Search Colors Follow the path into its depth until nothing is left to visit. a a c c b b Adjazenzliste Conceptual coloring of nodes g a c e f b d h i white: node has not been discovered yet. grey: node has been discovered and is marked for traversal / e e f f c e e d d f b b h being processed. black: node was discovered and entirely processed. f d i g g h h i i e Order a, b, c, f, d, e, g, h, i 329 330

Algorithm Depth First visit DFS-Visit( G, v ) Algorithm Depth First visit DFS-Visit( G ) Input: graph G = ( V, E ) Input: graph G = ( V, E ) , Knoten v . foreach v ∈ V do v.color ← grey v.color ← white foreach w ∈ N + ( v ) do if w.color = white then foreach v ∈ V do DFS-Visit( G, w ) if v.color = white then DFS-Visit(G,v) v.color ← black Depth First Search starting from node v . Running time (without Depth First Search for all nodes of a graph. Running time: Θ( | V | + � recursion): Θ(deg + v ) v ∈ V (deg + ( v ) + 1)) = Θ( | V | + | E | ) . 331 332 Interpretation of the Colors Breadth First Search When traversing the graph, a tree (or Forest) is built. When nodes are discovered there are three cases White node: new tree edge Grey node: Zyklus (“back-egde”) Black node: forward- / cross edge 333 334

Graph Traversal: Breadth First Search (Iterative) BFS-Visit( G, v ) Input: graph G = ( V, E ) Follow the path in breadth and only then descend into depth. Queue Q ← ∅ v.color ← grey a a c c b b Adjazenzliste enqueue ( Q, v ) g while Q � = ∅ do a c e f b d h i w ← dequeue ( Q ) foreach c ∈ N + ( w ) do e e f f d d c f e b b h i if c.color = white then c.color ← grey f d enqueue ( Q, c ) g g i i h h e w.color ← black Order a, b, d, e, c, f, g, h, i Algorithm requires extra space of O ( | V | ) . 335 336 Main program BFS-Visit( G ) Topological Sorting Input: graph G = ( V, E ) foreach v ∈ V do v.color ← white foreach v ∈ V do if v.color = white then BFS-Visit(G,v) Breadth First Search for all nodes of a graph. Running time: Θ( | V | + | E | ) . Evaluation Order? 337 338

Topological Sorting (Counter-)Examples Topological Sorting of an acyclic directed graph G = ( V, E ) : Unterhose Hose 1 Bijective mapping ord : V → { 1 , . . . , | V |} 2 5 Socken Schuhe Mantel such that ord( v ) < ord( w ) ∀ ( v, w ) ∈ E. Unterhemd Pullover Uhr 3 4 Identify i with Element v i := ord 1 ( i ) . Topological sorting � = A possible toplogical sorting of the graph: Cyclic graph: cannot be sorted topologically. Unterhemd,Pullover,Unterhose,Uhr,Hose,Mantel,Socken,Schuhe � v 1 , . . . , v | V | � . 339 340 Observation Inductive Proof Opposite Direction Base case ( n = 1 ): Graph with a single node without loop can be sorted topologically, set ord( v 1 ) = 1 . Theorem A directed graph G = ( V, E ) permits a topological sorting if and only Hypothesis: Graph with n nodes can be sorted topologically Step ( n → n + 1 ): if it is acyclic. 1 G contains a node v q with in-degree deg − ( v q ) = 0 . Otherwise iteratively Proof “ ⇒ ”: If G contains a cycle it cannot permit a topological follow edges backwards – after at most n + 1 iterations a node would be sorting, because in a cycle � v i 1 , . . . , v i m � it would hold that revisited. Contradiction to the cycle-freeness. Graph without node v q and without its edges can be topologically sorted v i 1 < · · · < v i m < v i 1 . 2 by the hypothesis. Now use this sorting and set ord( v i ) ← ord( v i ) + 1 for all i � = q and set ord( v q ) ← 1 . 341 342