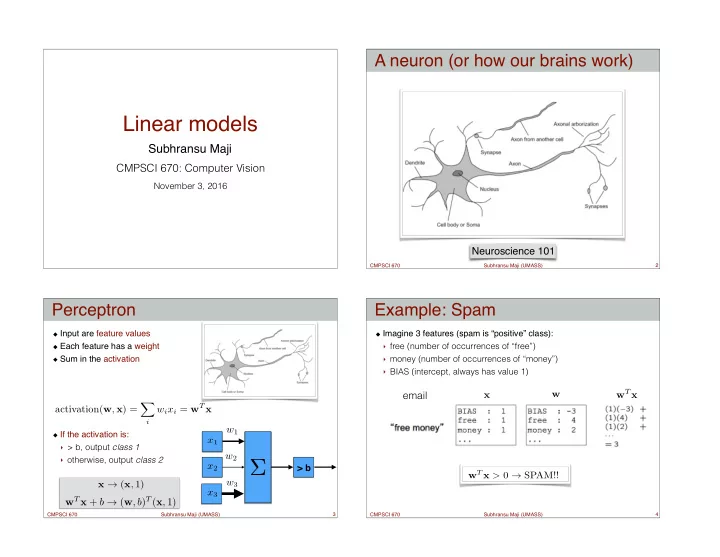

A neuron (or how our brains work) Linear models Subhransu Maji CMPSCI 670: Computer Vision November 3, 2016 Neuroscience 101 CMPSCI 670 Subhransu Maji (UMASS) 2 Perceptron Example: Spam Input are feature values Imagine 3 features (spam is “positive” class): Each feature has a weight ‣ free (number of occurrences of “free”) Sum in the activation ‣ money (number of occurrences of “money”) ‣ BIAS (intercept, always has value 1) w T x email w x X w i x i = w T x activation( w , x ) = i w 1 If the activation is: x 1 ‣ > b, output class 1 w 2 ‣ otherwise, output class 2 Σ x 2 > b w T x > 0 → SPAM!! x → ( x , 1) w 3 x 3 w T x + b → ( w , b ) T ( x , 1) CMPSCI 670 Subhransu Maji (UMASS) 3 CMPSCI 670 Subhransu Maji (UMASS) 4
Geometry of the perceptron Learning a perceptron Input: training data ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) In the space of feature vectors ‣ examples are points (in D dimensions) Perceptron training algorithm [Rosenblatt 57] ‣ an weight vector is a hyperplane (a D-1 dimensional object) w ← [0 , . . . , 0] Initialize ‣ One side corresponds to y=+1 for iter = 1,…,T y i x ‣ Other side corresponds to y=-1 w ‣ for i = 1,..,n x i Perceptrons are also called as linear classifiers • predict according to the current model ⇢ if w T x i > 0 +1 y i = ˆ if w T x i ≤ 0 w − 1 • if , no change y i = ˆ y i y i = − 1 • else, w ← w + y i x i w T x = 0 error driven, online, activations increase for +, randomize CMPSCI 670 Subhransu Maji (UMASS) 5 CMPSCI 670 Subhransu Maji (UMASS) 6 Properties of perceptrons Limitations of perceptrons Separability: some parameters will classify Convergence: if the data isn’t separable, the training data perfectly the training algorithm may not terminate ‣ noise can cause this ‣ some simple functions are not Convergence: if the training data is separable then the perceptron training will eventually separable (xor) converge [Block 62, Novikoff 62] Mediocre generation: the algorithm Mistake bound: the maximum number of finds a solution that “barely” separates mistakes is related to the margin the data assuming, || x i || ≤ 1 Overtraining: test/validation accuracy rises and then falls 1 #mistakes < δ 2 ‣ Overtraining is a kind of overfitting ⇥ y i w T x i ⇤ δ = max w min ( x i ,y i ) such that, || w || = 1 CMPSCI 670 Subhransu Maji (UMASS) 7 CMPSCI 670 Subhransu Maji (UMASS) 8
Overview Learning as optimization Linear models ‣ Perceptron: model and learning algorithm combined as one 1 [ y n w T x n < 0] + λ R ( w ) X min ‣ Is there a better way to learn linear models? w n We will separate models and learning algorithms fewest mistakes ‣ Learning as optimization } model design ‣ Surrogate loss function The perceptron algorithm will find an optimal w if the data is separable ‣ Regularization ‣ efficiency depends on the margin and norm of the data ‣ Gradient descent } optimization However, if the data is not separable, optimizing this is NP-hard ‣ Batch and online gradients ‣ i.e., there is no efficient way to minimize this unless P=NP ‣ Subgradient descent ‣ Support vector machines CMPSCI 670 Subhransu Maji (UMASS) 9 CMPSCI 670 Subhransu Maji (UMASS) 10 Learning as optimization Learning as optimization hyperparameter hyperparameter 1 [ y n w T x n < 0] + λ R ( w ) 1 [ y n w T x n < 0] + λ R ( w ) X X min min w w n n fewest mistakes simpler model fewest mistakes simpler model In addition to minimizing training error, we want a simpler model The questions that remain are: ‣ Remember our goal is to minimize generalization error ‣ What are good ways to adjust the optimization problem so that there are efficient algorithms for solving it? ‣ Recall the bias and variance tradeoff for learners ‣ What are good regularizations R( w ) for hyperplanes? We can add a regularization term R( w ) that prefers simpler models ‣ Assuming that the optimization problem can be adjusted ‣ For example we may prefer decision trees of shallow depth appropriately, what algorithms exist for solving the regularized Here λ is a hyperparameter of optimization problem optimization problem? CMPSCI 670 Subhransu Maji (UMASS) 11 CMPSCI 670 Subhransu Maji (UMASS) 12
Convex surrogate loss functions Weight regularization Zero/one loss is hard to optimize What are good regularization functions R( w ) for hyperplanes? concave ‣ Small changes in w can cause large changes in the loss We would like the weights — Surrogate loss: replace Zero/one loss by a smooth function ‣ To be small — ➡ Change in the features cause small change to the score ‣ Easier to optimize if the surrogate loss is convex convex ➡ Robustness to noise Examples: y ← w T x ‣ To be sparse — 9 y = +1 ˆ Zero/one Hinge 8 ➡ Use as few features as possible Logistic Exponential 7 ➡ Similar to controlling the depth of a decision tree Squared 6 This is a form of inductive bias Prediction 5 4 3 2 1 0 − 2 − 1.5 − 1 − 0.5 0 0.5 1 1.5 2 2.5 3 Loss CMPSCI 670 Subhransu Maji (UMASS) 13 CMPSCI 670 Subhransu Maji (UMASS) 14 Weight regularization Contours of p-norms convex for p ≥ 1 Just like the surrogate loss function, we would like R( w ) to be convex Small weights regularization sX R (norm) ( w ) = X w 2 R (sqrd) ( w ) = w 2 d d d d Sparsity regularization X R (count) ( w ) = not convex 1 [ | w d | > 0] d Family of “p-norm” regularization ! 1 /p X R (p-norm) ( w ) = | w d | p d http://en.wikipedia.org/wiki/Lp_space CMPSCI 670 Subhransu Maji (UMASS) 15 CMPSCI 670 Subhransu Maji (UMASS) 16
Contours of p-norms General optimization framework hyperparameter not convex for 0 ≤ p < 1 X y n , w T x n � � min ` + � R ( w ) w n p = 2 surrogate loss regularization 3 Select a suitable: ‣ convex surrogate loss ‣ convex regularization Counting non-zeros: Select the hyperparameter λ Minimize the regularized objective with respect to w p = 0 This framework for optimization is called Tikhonov regularization or generally Structural Risk Minimization (SRM) X R (count) ( w ) = 1 [ | w d | > 0] d http://en.wikipedia.org/wiki/Tikhonov_regularization http://en.wikipedia.org/wiki/Lp_space CMPSCI 670 Subhransu Maji (UMASS) 17 CMPSCI 670 Subhransu Maji (UMASS) 18 Optimization by gradient descent Choice of step size Good step size Convex function The step size is important — ‣ too small: slow convergence p 1 g ( k ) r p F ( p ) | p k p 1 p 2 ‣ too large: no convergence compute gradient at the current location p 2 η 1 p 3 A strategy is to use large step sizes initially step size η 1 p 3 p 4 p k +1 ← p k − η k g ( k ) and small step sizes later: p 5 p 6 η 2 p 4 take a step down the gradient η t ← η 0 / ( t 0 + t ) p 5 p 6 η 3 local optima = global optima There are methods that converge faster by Non-convex function Bad step size adapting step size to the curvature of the function η 1 p 1 p 2 ‣ Field of convex optimization p 3 p 4 local optima p 5 p 6 global optima http://stanford.edu/~boyd/cvxbook/ CMPSCI 670 Subhransu Maji (UMASS) 19 CMPSCI 670 Subhransu Maji (UMASS) 20
Example: Exponential loss Batch and online gradients X L ( w ) = L n ( w ) objective exp( − y n w T x n ) + λ X 2 || w || 2 L ( w ) = objective n n w ← w − η d L gradient descent d L X − y n x n exp( − y n w T x n ) + λ w d w d w = gradient n batch gradient online gradient X ! − y n x n exp( − y n w T x n ) + λ w w ← w − η update X ! d L n ✓ d L n ◆ w ← w − η n w ← w − η d w d w n regularization term loss term w ← (1 − ηλ ) w w ← w + cy n x n sum of n gradients gradient at n th point update weight after you see all points update weights after you see each point high for misclassified points shrinks weights towards zero similar to the perceptron update rule! Online gradients are the default method for multi-layer perceptrons CMPSCI 670 Subhransu Maji (UMASS) 21 CMPSCI 670 Subhransu Maji (UMASS) 22 Subgradient Example: Hinge loss ` (hinge) ( y, w T x ) = max(0 , 1 − y w T x ) max(0 , 1 − y n w T x n ) + λ X 2 || w || 2 L ( w ) = objective z n d L − 1 [ y n w T x n ≤ 1] y n x n + λ w X d w = subgradient n z X ! 1 − 1 [ y n w T x n ≤ 1] y n x n + λ w w ← w − η update subgradient n The hinge loss is not differentiable at z=1 regularization term loss term Subgradient is any direction that is below the function w ← w + η y n x n w ← (1 − ηλ ) w For the hinge loss a possible subgradient is: ⇢ if y w T x > 1 0 y n w T x n ≤ 1 d ` hinge only for points shrinks weights towards zero = d w otherwise − y x perceptron update y n w T x n ≤ 0 CMPSCI 670 Subhransu Maji (UMASS) 23 CMPSCI 670 Subhransu Maji (UMASS) 24
Recommend
More recommend