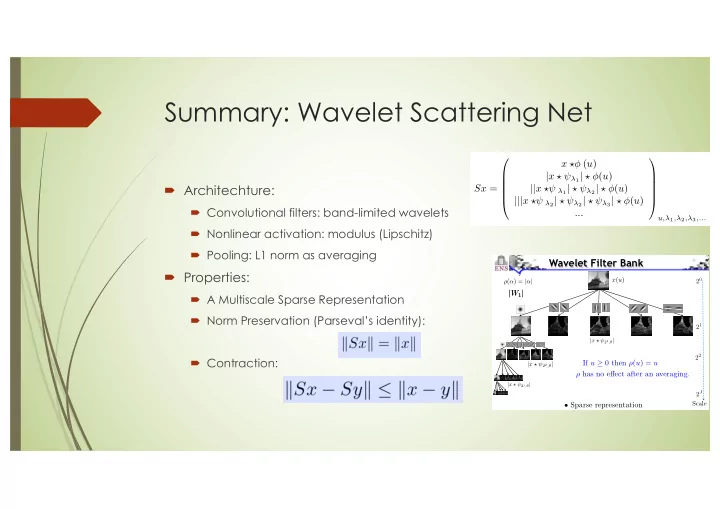
Summary: Wavelet Scattering Net x ( u ) | x 1 | ( u ) - PowerPoint PPT Presentation

Summary: Wavelet Scattering Net   x ⇤� ( u ) | x ⇤ ⇥ λ 1 | ⇤ � ( u )   ´ Architechture:   || x ⇤⇥ λ 1 | ⇤ ⇥ λ 2 | ⇤ � ( u ) Sx =     ||| x ⇤⇥ λ 2 | ⇤ ⇥ λ 2 | ⇤ ⇥ λ 3 | ⇤ � ( u )   ´ Convolutional filters: band-limited wavelets ... u, λ 1 , λ 2 , λ 3 ,... ´ Nonlinear activation: modulus (Lipschitz) is ´ Pooling: L1 norm as averaging Wavelet Filter Bank k ´ Properties: x ( u ) 2 0 ρ ( α ) = | α | k | W 1 | | W 1 | ´ A Multiscale Sparse Representation )) ´ Norm Preservation (Parseval’s identity): 2 1 k | x ? 2 1 , θ | 2 2 ´ Contraction: If u ≥ 0 then ρ ( u ) = u | x ? 2 2 , θ | Sx ρ has no e ff ect after an averaging. | x ? 2 j , θ | 2 J • Sparse representation Scale

Invariants/Stability of Scattering Net ´ Translation Invariance: • The average | x ? λ 1 | ? � ( t ) is invariant to small translations relatively to the support of φ . Z φ → 1 | x ? λ 1 | ? � ( t ) = lim | x ? λ 1 ( u ) | du = k x ? λ 1 k 1 ´ Stable Small Deformations:

Feature Extraction

Digit Classification: MNIST Joan Bruna Supervised y = f ( x ) S J x x Linear classifier Invariants to specific deformations Invariants to translations Separates di ff erent patterns Linearises small deformations No learning Classification Errors Training size Conv. Net. Scattering 50000 0 . 4% 0 . 4% LeCun et. al.

Other Invariants? General Convolutional Neural Networks?

Rotation and Scaling Invariance Laurent Sifre UIUC database: 25 classes Scattering classification errors Training Scat. Translation 20 20 %

Deep Convolutional Trees x J ( u, k J ) x 2 ( u, k 2 ) x ( u ) x 1 ( u, k 1 ) ρ L J classification ρ L 1 k 1 k 2 x j = ρ L j x j − 1 L j is composed of convolutions and subs samplings: ⇣ ⌘ x j ( u, k j ) = ⇢ x j − 1 ( · , k ) ? h k j ,k ( u ) No channel communication: what limitations ?

Deep Convolutional Networks x J ( u, k J ) x 2 ( u, k 2 ) x ( u ) x 1 ( u, k 1 ) ρ L J classification ρ L 1 k 1 k 2 x j = ρ L j x j − 1 • L j is a linear combination of convolutions and subsampling: ⇣ X ⌘ x j ( u, k j ) = ⇢ x j − 1 ( · , k ) ? h k j ,k ( u ) k sum across channels What is the role of channel connections ? Linearize other symmetries beyond translations.

Rotation Invariance • Channel connections linearize other symmetries. | W 1 | θ | x ? 2 1 , θ | 2 J | x ? 2 2 , θ | x ? � J | x ? 2 3 , θ | Scale • Invariance to rotations are computed by convolutions along the rotation variable θ with wavelet filters. ⇒ invariance to rigid mouvements.

Wavelet Transform on a Group Laurent Sifre • Roto-translation group G = { g = ( r, t ) ∈ SO (2) × R 2 } ( r, t ) . x ( u ) = x ( r − 1 ( u − t )) Z 0 � 1 g ) dg 0 X ( g 0 ) φ ( g • Averaging on G : X ~ φ ( g ) = G ✓ ◆ X ~ φ ( g ) • Wavelet transform on G : W 2 X = . X ~ ψ λ 2 ( g ) λ 2 ,g translation roto-translation | W 1 | | W 2 | | x ? 2 j r ( t ) | = X j ( r, t ) | X j ~ ψ λ 2 ( r, t ) | x x ? � ( t ) X j ~ φ ( r, t )

Wavelet Transform on a Group Laurent Sifre • Roto-translation group G = { g = ( r, t ) ∈ SO (2) × R 2 } ( r, t ) . x ( u ) = x ( r − 1 ( u − t )) Z 0 � 1 g ) dg 0 X ( g 0 ) φ ( g • Averaging on G : X ~ φ ( g ) = G ✓ ◆ X ~ φ ( g ) • Wavelet transform on G : W 2 X = . X ~ ψ λ 2 ( g ) λ 2 ,g scalo-roto-translation translation + renormalization = X (2 j , r, t ) | W 1 | | W 2 | | x ? 2 j r ( t ) | | X ~ ψ λ 2 (2 j , r, t ) | x x ? � ( t ) X ~ φ (2 j , r, t )

Rotation and Scaling Invariance Laurent Sifre UIUC database: 25 classes Scattering classification errors Training Translation Transl + Rotation + Scaling 20 20 % 2% 0.6 %

Wiatowski-Bolcskei’15 ´ Scattering Net by Mallat et al. so far ´ Wavelet Linear filter ´ Nonlinear activation by modulus ´ Average pooling ´ Generalization by Wiatowski-Bolcskei’15 ´ Filters as frames ´ Lipschitz continuous Nonlinearities ´ General Pooling: Max/Average/Nonlinear, etc.

Generalization of Wiatowski-Bolcskei’15 Scattering networks ([ Mallat, 2012 ], [ Wiatowski and HB, 2015 ]) || f ∗ g λ ( k ) 1 | ∗ g λ ( l ) 2 | || f ∗ g λ ( p ) 1 | ∗ g λ ( r ) 2 | · ∗ χ 3 · ∗ χ 3 | f ∗ g λ ( k ) 1 | | f ∗ g λ ( p ) 1 | · ∗ χ 2 · ∗ χ 2 feature map f · ∗ χ 1 feature vector Φ ( f ) General scattering networks guarantee [ Wiatowski & HB, 2015 ] - (vertical) translation invariance - small deformation sensitivity essentially irrespective of filters, non-linearities, and poolings!

Wavelet basis -> filter frame Building blocks Basic operations in the n -th network layer ´ g λ ( k ) pool. non-lin. n . . f . g λ ( r ) pool. non-lin. n Filters : Semi-discrete frame Ψ n := { χ n } [ { g λ n } λ n ∈ Λ n k f ⇤ g λ n k 2  B n k f k 2 A n k f k 2 2  k f ⇤ χ n k 2 X 8 f 2 L 2 ( R d ) 2 + 2 , λ n ∈ Λ n e.g.: Structured filters

Frames: random or learned filters Building blocks Building blocks Basic operations in the n -th network layer Basic operations in the n -th network layer g λ ( k ) g λ ( k ) pool. pool. non-lin. non-lin. n n . . . . f f . . g λ ( r ) g λ ( r ) pool. non-lin. pool. non-lin. n n Filters : Semi-discrete frame Ψ n := { χ n } [ { g λ n } λ n ∈ Λ n Filters : Semi-discrete frame Ψ n := { χ n } [ { g λ n } λ n ∈ Λ n k f ⇤ g λ n k 2  B n k f k 2 k f ⇤ g λ n k 2  B n k f k 2 X A n k f k 2 2  k f ⇤ χ n k 2 X 8 f 2 L 2 ( R d ) A n k f k 2 2  k f ⇤ χ n k 2 8 f 2 L 2 ( R d ) 2 + 2 , 2 + 2 , λ n ∈ Λ n λ n ∈ Λ n e.g.: Unstructured filters e.g.: Learned filters

Nonlinear activations Building blocks Basic operations in the n -th network layer g λ ( k ) pool. non-lin. n . . f . g λ ( r ) pool. non-lin. n Non-linearities : Point-wise and Lipschitz-continuous 8 f, h 2 L 2 ( R d ) k M n ( f ) � M n ( h ) k 2  L n k f � h k 2 , ) Satisfied by virtually all non-linearities used in the deep learning literature ! ReLU: L n = 1 ; modulus: L n = 1 ; logistic sigmoid: L n = 1 4 ; ...

Pooling Building blocks Basic operations in the n -th network layer g λ ( k ) pool. non-lin. n . . f . g λ ( r ) pool. non-lin. n Pooling : In continuous-time according to f 7! S d/ 2 P n ( f )( S n · ) , n where S n � 1 is the pooling factor and P n : L 2 ( R d ) ! L 2 ( R d ) is R n -Lipschitz-continuous ) Emulates most poolings used in the deep learning literature ! e.g.: Pooling by sub-sampling P n ( f ) = f with R n = 1 e.g.: Pooling by averaging P n ( f ) = f ⇤ φ n with R n = k φ n k 1

Vertical translation invariance Theorem (Wiatowski and HB, 2015) Assume that the filters, non-linearities, and poolings satisfy B n  min { 1 , L − 2 n R − 2 n } , 8 n 2 N . Let the pooling factors be S n � 1 , n 2 N . Then, ✓ k t k ◆ ||| Φ n ( T t f ) � Φ n ( f ) ||| = O , S 1 . . . S n for all f 2 L 2 ( R d ) , t 2 R d , n 2 N . The condition B n  min { 1 , L − 2 n R − 2 n } , 8 n 2 N , is easily satisfied by normalizing the filters { g λ n } λ n ∈ Λ n .

Vertical translation invariance Theorem (Wiatowski and HB, 2015) Assume that the filters, non-linearities, and poolings satisfy B n  min { 1 , L − 2 n R − 2 n } , 8 n 2 N . Let the pooling factors be S n � 1 , n 2 N . Then, ✓ k t k ◆ ||| Φ n ( T t f ) � Φ n ( f ) ||| = O , S 1 . . . S n for all f 2 L 2 ( R d ) , t 2 R d , n 2 N . ) Features become more invariant with increasing network depth !

Vertical translation invariance Theorem (Wiatowski and HB, 2015) Assume that the filters, non-linearities, and poolings satisfy B n  min { 1 , L − 2 n R − 2 n } , 8 n 2 N . Let the pooling factors be S n � 1 , n 2 N . Then, ✓ ◆ k t k ||| Φ n ( T t f ) � Φ n ( f ) ||| = O , S 1 . . . S n for all f 2 L 2 ( R d ) , t 2 R d , n 2 N . Full translation invariance : If lim n →∞ S 1 · S 2 · . . . · S n = 1 , then n →∞ ||| Φ n ( T t f ) � Φ n ( f ) ||| = 0 lim

Philosophy behind invariance results Mallat’s “horizontal” translation invariance [ Mallat, 2012 ]: ∀ f ∈ L 2 ( R d ) , ∀ t ∈ R d J →∞ ||| Φ W ( T t f ) − Φ W ( f ) ||| = 0 , lim - features become invariant in every network layer, but needs J → ∞ - applies to wavelet transform and modulus non-linearity without pooling “Vertical” translation invariance: n →∞ ||| Φ n ( T t f ) − Φ n ( f ) ||| = 0 , ∀ f ∈ L 2 ( R d ) , ∀ t ∈ R d lim - features become more invariant with increasing network depth - applies to general filters, general non-linearities, and general poolings

Non-linear deformations Non-linear deformation ( F τ f )( x ) = f ( x − τ ( x )) , where τ : R d → R d For “small” τ :

Non-linear deformations Non-linear deformation ( F τ f )( x ) = f ( x − τ ( x )) , where τ : R d → R d For “large” τ :

Deformation sensitivity for signal classes Consider ( F τ f )( x ) = f ( x − τ ( x )) = f ( x − e − x 2 ) f 1 ( x ) , ( F τ f 1 )( x ) x f 2 ( x ) , ( F τ f 2 )( x ) x For given τ the amount of deformation induced can depend drastically on f ∈ L 2 ( R d )