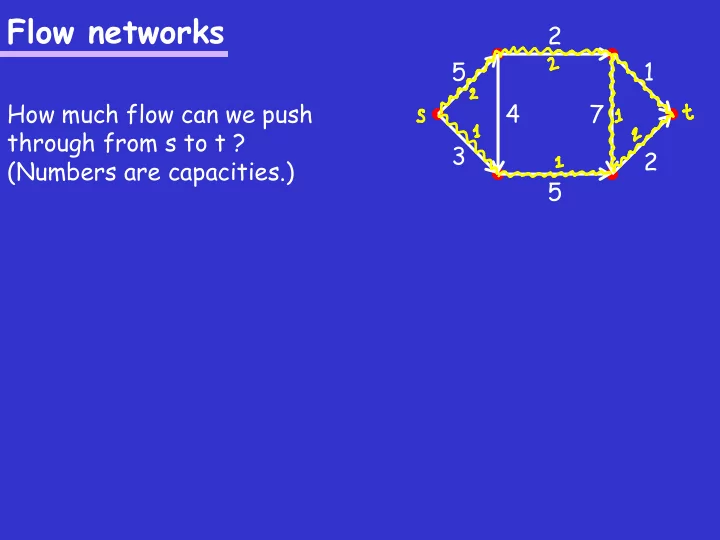
Flow networks 2 5 1 How much flow can we push 4 7 through from - PowerPoint PPT Presentation

Flow networks 2 5 1 How much flow can we push 4 7 through from s to t ? 3 2 (Numbers are capacities.) 5

2 Flow networks 5 1 s 4 7 t 3 2 5 Def: A flow network is a directed graph G=(V,E) where edges have capacities c:E->R + . There are two specified vertices s (source) and t (sink). A flow f:E->R must satisfy: • Capacity constraint : for every edge e: f(e) · c(e) • Flow conservation : for every v in V-{s,t}:  e out of v f(e) =  e into v f(e) The value of the flow is:  e out of s f(e) -  e into s f(e)

Maximum flow problem Input: 2 5 1 a flow network G=(V,E), with capacities c, the source s and sink t s 4 7 t Output: 3 2 5 a maximum-value flow Algorithm ?

Maximum flow problem – Ford-Fulkerson “Def”: 2 5 1 Given a flow f, an augmenting path is a path s=v 1 , v 2 , …, v k =t such that s 4 2 t f(v i ,v i+1 ) < c(v i ,v i+1 ) for i=1,…,k -1 3 7 5 Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson “Def”: 2 5 1 Given a flow f, an augmenting path is a path s=v 1 , v 2 , …, v k =t such that s 4 2 t f(v i ,v i+1 ) < c(v i ,v i+1 ) for i=1,…,k -1 3 7 5 How to find augmenting paths ? Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson “Def”: 2 5 1 Given is G=(V,E), c, f. The residual graph has edges s 4 2 t weighted by the residual capacities , 3 7 i.e. c f (e) = c(e)-f(e) 5 Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson “Def”: 2 5 1 Given is G=(V,E), c, f. The residual graph has edges s 4 2 t weighted by the residual capacities , 3 7 i.e. c f (e) = c(e)-f(e) 5 Idea: Find an s-t path in the residual graph! Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson Consider this input: 1000 1000 s 1 t 1000 1000 Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson Consider this input: 1000 1000 s 1 t Need to refine the definition of augmenting paths and 1000 1000 residual graph. Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson Refined def: 1000 1000 Given is G=(V,E), c, f. The residual graph G f =(V,E’) s 1 t contains the following edges: 1000 1000 • forward edge : if e 2 E and f(e) < c(e) then include e in E’ with weight c f (e) = c(e)-f(e), • backward edge : if e=(u,v) 2 E with f(e)>0 then include (v,u) in E’ with weight c f (v,u) = f(u,v).

Maximum flow problem – Ford-Fulkerson Ford-Fulkerson ( G=(V,E), c, s, t ) 1. For every edge e let f(e)=0 2. Construct the residual graph G f 3. While exists s-t path in G f do 4. Let p be an s-t path in G f 5. Let d=min e in p c f (e) 6. For every e on p do 7. If e is a forward edge then 8. f(e)+=d 9. else 10. f(reverse(e))-=d 11. Update G f (construct new G f ) 12.Return f

Maximum flow problem – Ford-Fulkerson Ford-Fulkerson ( G=(V,E), c, s, t ) Running 1. For every edge e let f(e)=0 time: 2. Construct the residual graph G f 3. While exists s-t path in G f do 4. Let p be an s-t path in G f 5. Let d=min e in p c f (e) 6. For every e on p do 7. If e is a forward edge then 8. f(e)+=d 9. else 10. f(reverse(e))-=d 11. Update G f (construct new G f ) 12.Return f

Maximum flow problem – Ford-Fulkerson Consider this input: 1000 1000 s 1 t 1000 1000

Maximum flow problem – Ford-Fulkerson Lemma: 2 5 1 Ford-Fulkerson works. s 4 7 t 3 7 5 Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Maximum flow problem – Ford-Fulkerson Lemma: 2 5 1 Ford-Fulkerson works. s 4 7 t Def: 3 7 Given G=(V,E), c. An s-t cut of G is 5 a subset of vertices S s.t. s 2 S and t 2 S C . Its value is  e out of S c(e)

Maximum flow problem – Ford-Fulkerson Lemma: 2 5 1 Ford-Fulkerson works. s 4 7 t 3 7 The Max-flow min-cut theorem: 5 Let min-cut(G) be the minimal value of an s-t cut of G. Then: f is a maximum flow iff value(f)=min-cut(G)

Improving Ford-Fulkerson Can find better paths to reduce 2 the running time? 5 1 s 4 7 t 3 7 5 Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Improving Ford-Fulkerson Can find better paths to reduce 2 the running time? 5 1 - many ways, will discuss two: s 4 7 t - Scaling paths 3 2 5 - BFS Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Improving Ford-Fulkerson Can find better paths to reduce 2 the running time? 5 1 - many ways, will discuss two: s 4 7 t - Scaling paths 3 2 5 Ford-Fulkerson ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augmenting path p do 3. Augment flow f along p 4. Return f

Improving Ford-Fulkerson Can find better paths to reduce 2 the running time? 5 1 - many ways, will discuss two: s 4 7 t - Scaling paths 3 2 5 - BFS Thm: Edmonds-Karp takes O(|V||E|) iterations. Running time of Edmonds-Karp: Edmonds-Karp ( G=(V,E), c, s, t ) 1. Initialize flow f to 0 2. While exists augm. path p (check with BFS) do 3. Augment flow f along p 4. Return f

Applications of Network Flows • multiple sources, multiple sinks s 1 t 1 t 2 s 2 t 3 s 3 t 4

Applications of Network Flows • how to find minimum cut 2 5 1 s 4 7 t 3 7 5

Applications of Network Flows • maximum number of edge-disjoint s-t paths s t

Applications of Network Flows • maximum bipartite matching

Applications of Network Flows • maximum bipartite matching

Applications of Network Flows • maximum weighted (perfect) bipartite matching 7 5 2 3 4 4 1 6 3 8

Introduction to Linear Programming Consider the Diet problem: - n food items, m nutrients - for every nutrient: the daily quota b j - for each item: cost per pound c i - for every item and nutrient: how much of the nutrient in a pound of item: a i,j

Introduction to Linear Programming A linear program looks like this: Find x 1 , x 2 , …, x m which • maximize c 1 x 1 + c 2 x 2 + … + c m x m • and satisfy these constraints: a 1,1 x 1 + a 1,2 x 2 + … + a 1,m x m · b 1 a 2,1 x 1 + a 2,2 x 2 + … + a 2,m x m · b 2 … a n,1 x 1 + a n,2 x 2 + … + a n,m x m · b n

Introduction to Linear Programming A linear program in compressed form: Given a vector c in R m , a vector b in R n and a matrix A in R n x m , find a vector x in R m which satisfies xA T · b and maximizes cx T . Thm: Exists a polynomial-time algorithm solving linear programs. Caveat: Sometimes need integer programs (no algorithm for integer programs is likely to exist) !