Elliptic curve arithmetic 2 1 ECC school, Nijmegen, 9-11 - PowerPoint PPT Presentation

Elliptic curve arithmetic 𝑄 2 𝑄 1 ECC school, Nijmegen, 9-11 November 2017 Wouter Castryck 𝑄 1 + 𝑄 2

Tangent-chord arithmetic on cubic curves

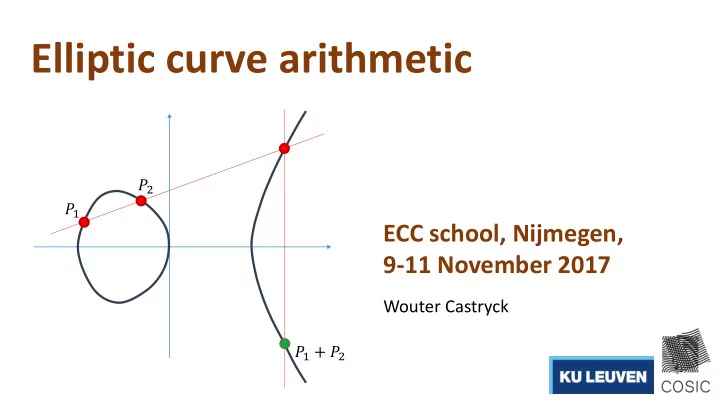
Introduction Consequence of Bézout ’s theorem: on a cubic curve 𝐷 ∶ 𝑔 𝑦, 𝑧 = σ 𝑗+𝑘=3 𝑏 𝑗𝑘 𝑦 𝑗 𝑧 𝑘 = 0 , new points can be constructed from known points using tangents and chords. Pierre de Fermat 𝑔 𝑦, 𝑧 = 0 This principle was already known to 17 th century natives like Fermat and Newton . Isaac Newton

Introduction This construction was known to respect the base field . This means: if 𝑔 𝑦, 𝑧 ∈ 𝑙[𝑦, 𝑧] with 𝑙 some field, and one starts from points having coordinates in 𝑙 , then new points obtained through the tangent-chord method also have coordinates in 𝑙 . 𝑔 𝑦, 𝑧 = 0 Informal reason: Consider two points on the 𝑦 -axis 𝑄 1 = 𝑏, 0 and 𝑄 2 = (𝑐, 0) . 𝑄 1 Then the “ chord ” is 𝑧 = 0 . 𝑄 2 The intersection is computed by 𝑔 𝑦, 0 = 𝑦 − 𝑏 ⋅ 𝑦 − 𝑐 ⋅ linear factor always has a root over 𝒍 !

Introduction Thus: tangents and chords give some sort of composition law on the set of 𝑙 -rational points of a cubic curve. Later it was realized that by adding in a second step, this gives the curve an abelian group structure! only after an incredible historical detour which took more than 200 years … choose a base point 𝑄 𝑄 1 + 𝑄 2 𝑃 𝑄 2𝑄 2 commutativity : 𝑄 1 + 𝑄 2 = 𝑄 2 + 𝑄 1 Henri Poincaré 𝑄 associativity : 1 𝑄 1 + 𝑄 2 + 𝑄 3 = 𝑄 1 + (𝑄 2 + 𝑄 3 ) neutral element : 𝑄 + 𝑃 = 𝑄 inverse element : First formalized by Poincaré in 1901. ∃ −𝑄 ∶ 𝑄 + −𝑄 = 𝑃

Introduction 𝑨 = 0 Conditions for this to work: 1) One should work projectively (as opposed to affinely): Homogenize 𝑔 𝑦, 𝑧 = σ 𝑗+𝑘=3 𝑏 𝑗𝑘 𝑦 𝑗 𝑧 𝑘 to 𝐺 𝑦, 𝑧, 𝑨 = σ 𝑗+𝑘=3 𝑏 𝑗𝑘 𝑦 𝑗 𝑧 𝑘 𝑨 3−𝑗−𝑘 and consider points 𝑦: 𝑧: 𝑨 ≠ (0: 0: 0) , up to scaling. Two types of points: affine points points at infinity 𝑨 ≠ 0 : the point is of the form (𝑦: 𝑧: 1) 𝑨 = 0: points of the form (𝑦: 𝑧: 0) up to scaling. But then 𝑦, 𝑧 is an affine point! (Up to three such points.)

Introduction Conditions for this to work:  2) The curve should be smooth , meaning that 𝑔 = 𝜖𝑔 𝜖𝑦 = 𝜖𝑔 𝜖𝑧 = 𝜖𝑔 𝜖𝑨 = 0  has no solutions. This ensures that every point 𝑄 has a well-defined tangent line 𝑈 ∶ 𝜖𝑔 𝜖𝑦 𝑄 ⋅ 𝑦 + 𝜖𝑔 𝜖𝑧 𝑄 ⋅ 𝑧 + 𝜖𝑔 𝜖𝑨 𝑄 ⋅ 𝑨 = 0. 

Introduction Conditions for this to work: 3) 𝑃 should have coordinates in 𝑙 , in order for the arithmetic to work over 𝑙 . 𝑃 Definition: an elliptic curve over 𝑙 is a smooth projective cubic curve 𝐹/𝑙 equipped with a 𝑙 -rational base point 𝑃 . (Caution: there exist more general and less general definitions.) Under these assumptions we have as wanted: Tangent-chord arithmetic turns 𝐹 into an abelian group with neutral element 𝑃 . The set of 𝑙 -rational points 𝐹(𝑙) form a subgroup.

Exercises 1) Describe geometrically what it means to invert a point 𝑄 , i.e. to find a point −𝑄 such that 𝑄 + −𝑄 = 𝑃 . 2) Why does this construction simplify considerably if 𝑃 is a flex (= point at which its tangent line meets the curve triply)? 3) If 𝑃 is a flex then 𝑃 3𝑄 ≔ 𝑄 + 𝑄 + 𝑄 = 𝑃 if and only if 𝑄 is a flex. Explain why.

On the terminology “ elliptic curves”

On the terminology In the 18 th century, unrelated to all this, Fagnano and Euler revisited the unsolved problem of determining the circumference of an ellipse. ? Giulio Fagnano They got stuck on difficult integrals, now called elliptic integrals . Leonhard Euler

On the terminology In the 19 th century Abel and Jacobi studied the inverse functions of elliptic integrals. 𝑢 = 𝑔(𝑡) ? Niels H. Abel When viewed as complex functions, they observed doubly periodic behaviour: there exist 𝜕 1 , 𝜕 2 ∈ 𝐃 such that 𝑔 𝑨 + 𝜇 1 𝜕 1 + 𝜇 2 𝜕 2 = 𝑔 𝑨 for all 𝜇 1 , 𝜇 2 ∈ 𝐚 . Compare to: sin 𝑦 + 𝜇 ⋅ 2𝑙𝜌 = sin 𝑦 for all 𝜇 ∈ 𝐚, etc. Carl G. Jacobi Such generalized trigonometric functions became known as elliptic functions .

On the terminology In other words: elliptic functions on 𝐃 are well-defined modulo 𝐚𝜕 1 + 𝐚𝜕 2 . Mid 19 th century Weierstrass classified all elliptic functions for any given 𝜕 1 , 𝜕 2 , and used this to define a biholomorphism 𝜕 2 𝐃/(𝐚𝜕 1 + 𝐚𝜕 2 ) → 𝐹: 𝑨 ↦ (℘ 𝑨 , ℘′ 𝑨 ) 𝜕 1 to a certain algebraic curve 𝐹 … … which he called an elliptic curve! Note that 𝐃/(𝐚𝜕 1 + 𝐚𝜕 2 ) is an abelian group, almost by definition. The biholomorphism endows 𝐹 with the same group structure … … where it turns out to correspond to tangent-chord arithmetic! Karl Weierstrass

Weierstrass curves and their arithmetic

Weierstrass curves 𝑃 = (0: 1: 0) 𝑨 = 0 The concrete type of elliptic curves found by Weierstrass now carry his name. They are the most famous shapes of elliptic curves. Assume char 𝑙 ≠ 2,3 . Definition: a Weierstrass elliptic curve is defined by 𝑧 2 𝑨 = 𝑦 3 + 𝐵𝑦𝑨 2 + 𝐶𝑨 3 𝑧 2 = 𝑦 3 + 𝐵𝑦 + 𝐶 where 𝐵, 𝐶 ∈ 𝑙 satisfy 4𝐵 3 + 27𝐶 2 ≠ 0 . The base point 𝑃 is the unique point at infinity. (typical plot for 𝑙 = 𝐒 ) Can be shown: up to “ isomorphism ” every elliptic curve is Weierstrass.

Weierstrass curves Note: 𝑃 1) the lines through 𝑃 = (0: 1: 0) are the vertical lines (except for the line at infinity 𝑨 = 0 ). 2) The equation 𝑧 2 = 𝑦 3 + 𝐵𝑦 + 𝐶 is symmetric in 𝑧 . 𝑄 (𝑦, 𝑧) This gives a first feature: inverting a point on a Weierstrass curve is super easy! Indeed: if 𝑄 = (𝑦, 𝑧) is an affine point then (𝑦, −𝑧) −𝑄 = 𝑦, −𝑧 .

Weierstrass curves What about point addition? Write 𝑄 1 + 𝑄 2 = 𝑦 3 , 𝑧 3 . Line through 𝑄 1 = (𝑦 1 , 𝑧 1 ) and 𝑄 2 = (𝑦 2 , 𝑧 2 ) is 𝑄 𝜇 = 𝑧 2 −𝑧 1 𝑧 − 𝑧 1 = 𝜇 𝑦 − 𝑦 1 2 where 𝑦 2 −𝑦 1 . 𝑄 1 Substituting 𝑧 ← 𝑧 1 + 𝜇 𝑦 − 𝑦 1 in the curve equation 𝑦 3 + 𝐵𝑦 + 𝐶 − 𝑧 2 = 0 : 2 = 0 . 𝑦 3 + 𝐵𝑦 + 𝐶 − 𝑧 1 + 𝜇 𝑦 − 𝑦 1 𝑦 3 − 𝜇 2 𝑦 2 + ⋯ = 0 . 𝑦 3 + 𝐵𝑦 + 𝐶 − (𝜇 2 𝑦 2 + ⋯ ) = 0 . So, sum of the roots is 𝜇 2 . But 𝑦 1 , 𝑦 2 are roots! 𝑄 1 + 𝑄 We find: ቊ 𝑦 3 = 𝜇 2 − 𝑦 1 − 𝑦 2 2 𝑧 3 = −𝑧 1 − 𝜇(𝑦 3 − 𝑦 1 )

Weierstrass curves 𝑃 where 𝜇 = 𝑧 2 −𝑧 1 𝑦 2 −𝑦 1 . But what if 𝑦 1 = 𝑦 2 ? 𝑄 𝑄 2 Two cases: Either 𝑧 1 = 𝑧 2 ≠ 0 , i.e. 𝑄 1 = 𝑄 2 = 𝑄 . In this case we need to replace 𝜇 by 2 +2𝐵𝑦 1 𝑄 𝜇 = 3𝑦 1 1 . 2𝑧 1 2𝑄 Or 𝑧 1 = −𝑧 2 , in which case 𝑄 1 + 𝑄 2 = 𝑃 . We find: ቊ 𝑦 3 = 𝜇 2 − 𝑦 1 − 𝑦 2 Conclusion : formulas for computing on a Weierstrass curve are not too bad, but case distinctive. 𝑧 3 = −𝑧 1 − 𝜇(𝑦 3 − 𝑦 1 )

More efficient elliptic curve arithmetic? The Weierstrass addition formulas are reasonably good for several purposes … … but can they be boosted? Huge amount of activity starting in the 1980’s. One reason: Koblitz and Miller’s suggestion to use elliptic curves in crypto! agree on 𝐹/𝐆 𝑟 and 𝑄 ∈ 𝐹(𝐆 𝑟 ) chooses secret 𝒃 ∈ 𝐚 chooses secret 𝒄 ∈ 𝐚 Victor Miller computes 𝒃𝑄 computes 𝒄𝑄 receives receives computes 𝒃 𝒄𝑄 = 𝒃𝒄𝑄 computes 𝒄 𝒃𝑄 = 𝒃𝒄𝑄 (Example: Diffie-Hellman key exchange.) Initial reason: Lenstra’s elliptic curve method (ECM) for integer factorization. Neal Koblitz

Generic methods for efficient scalar multiplication

Efficient scalar multiplication The most important operation in both (discrete-log based) elliptic curve cryptography, the elliptic curve method for integer factorization, is scalar multiplication : given a point 𝑄 and a positive integer 𝑏 , compute 𝑏𝑄 ≔ 𝑄 + 𝑄 + ⋯ + 𝑄 𝑏 times. Note: adding 𝑄 consecutively to itself 𝑏 − 1 times is not an option ! in practice 𝑏 consists of hundreds of bits!

Efficient scalar multiplication: double-and-add Much better idea: double-and-add , walking through the binary expansion of 𝑏 . Toy example: replace the 15 additions in 16𝑄 = 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 + 𝑄 by the 4 doublings in 16𝑄 = 2 2 2 2𝑄 . General method: 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑𝑸 + 𝑸 + 𝑸 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑𝑸 + 𝑸 + 𝑸 𝟑 𝟑𝑸 + 𝑸 𝟑𝑸 𝑸 + 𝑸 𝑏 = 101100010 … 0101 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑𝑸 + 𝑸 + 𝑸 𝟑(𝟑 𝟑 𝟑 𝟑𝑸 + 𝑸 + 𝑸 ) 𝟑(𝟑 𝟑 𝟑𝑸 + 𝑸 + 𝑸) 𝟑 𝟑 𝟑𝑸 + 𝑸 + 𝑸 + 𝑸 Exercise : verify that this computes 𝑏𝑄 using 𝑃(log 𝑏) additions or doublings, as opposed to 𝑃(𝑏) . double and add double double and add double double and add double double double ( Horner’s rule, basically.)