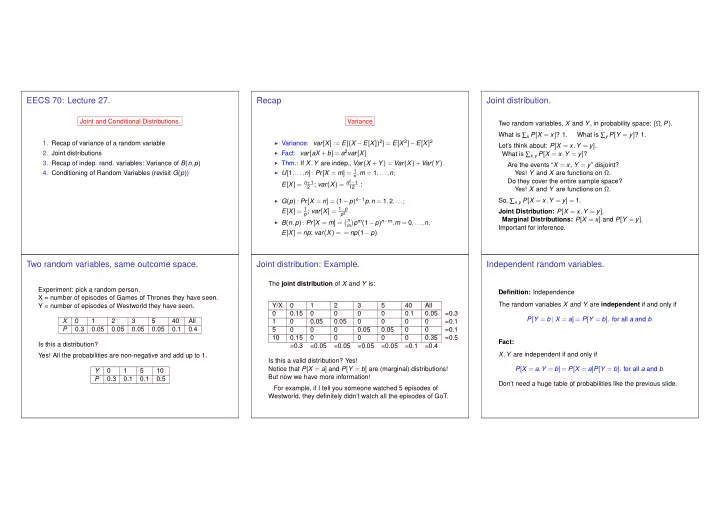

EECS 70: Lecture 27. Recap Joint distribution. Joint and Conditional Distributions. Variance Two random variables, X and Y , in probability space: (Ω , P ) . What is ∑ x P [ X = x ] ? 1. What is ∑ y P [ Y = y ] ? 1. ◮ Variance: var [ X ] := E [( X − E [ X ]) 2 ] = E [ X 2 ] − E [ X ] 2 1. Recap of variance of a random variable Let’s think about: P [ X = x , Y = y ] . ◮ Fact: var [ aX + b ] = a 2 var [ X ] 2. Joint distributions What is ∑ x , y P [ X = x , Y = y ] ? ◮ Thm.: If X , Y are indep., Var ( X + Y ) = Var ( X )+ Var ( Y ) . 3. Recap of indep. rand. variables: Variance of B ( n , p ) Are the events “ X = x , Y = y ” disjoint? ◮ U [ 1 ,..., n ] : Pr [ X = m ] = 1 4. Conditioning of Random Variables (revisit G ( p ) ) n , m = 1 ,..., n ; Yes! Y and X are functions on Ω . Do they cover the entire sample space? 2 ; var ( X ) = n 2 − 1 E [ X ] = n + 1 12 . ; Yes! X and Y are functions on Ω . ◮ G ( p ) : Pr [ X = n ] = ( 1 − p ) n − 1 p , n = 1 , 2 ,... ; So, ∑ x , y P [ X = x , Y = y ] = 1. p ; var [ X ] = 1 − p E [ X ] = 1 p 2 . Joint Distribution: P [ X = x , Y = y ] . Marginal Distributions: P [ X = x ] and P [ Y = y ] . � n p m ( 1 − p ) n − m , m = 0 ,..., n ; ◮ B ( n , p ) : Pr [ X = m ] = � m Important for inference. E [ X ] = np ; var ( X ) = = np ( 1 − p ) . Two random variables, same outcome space. Joint distribution: Example. Independent random variables. The joint distribution of X and Y is: Experiment: pick a random person. Definition: Independence X = number of episodes of Games of Thrones they have seen. The random variables X and Y are independent if and only if Y/X 0 1 2 3 5 40 All Y = number of episodes of Westworld they have seen. 0 0.15 0 0 0 0 0.1 0.05 =0.3 P [ Y = b | X = a ] = P [ Y = b ] , for all a and b . X 0 1 2 3 5 40 All 1 0 0.05 0.05 0 0 0 0 =0.1 P 0.3 0.05 0.05 0.05 0.05 0.1 0.4 5 0 0 0 0.05 0.05 0 0 =0.1 10 0.15 0 0 0 0 0 0.35 =0.5 Fact: Is this a distribution? =0.3 =0.05 =0.05 =0.05 =0.05 =0.1 =0.4 X , Y are independent if and only if Yes! All the probabilities are non-negative and add up to 1. Is this a valid distribution? Yes! Notice that P [ X = a ] and P [ Y = b ] are (marginal) distributions! P [ X = a , Y = b ] = P [ X = a ] P [ Y = b ] , for all a and b . Y 0 1 5 10 But now we have more information! P 0.3 0.1 0.1 0.5 Don’t need a huge table of probabilities like the previous slide. For example, if I tell you someone watched 5 episodes of Westworld, they definitely didn’t watch all the episodes of GoT.
Independence: examples. Mean of product of independent RVs. Variance of sum of two independent random variables Theorem: Theorem If X and Y are independent, then Let X , Y be independent RVs. Then Var ( X + Y ) = Var ( X )+ Var ( Y ) . E [ XY ] = E [ X ] E [ Y ] . Example 1 Proof: Since shifting the random variables does not change their variance, Roll two dices. X , Y = number of pips on the two dice. X , Y are let us subtract their means. independent. Proof: Recall that E [ g ( X , Y )] = ∑ x , y g ( x , y ) P [ X = x , Y = y ] . Hence, That is, we assume that E ( X ) = 0 and E ( Y ) = 0. Indeed: P [ X = a , Y = b ] = 1 / 36 , P [ X = a ] = P [ Y = b ] = 1 / 6 . Then, by independence, = ∑ xyP [ X = x , Y = y ] = ∑ E [ XY ] xyP [ X = x ] P [ Y = y ] , by ind. Example 2 x , y x , y Roll two dices. X = total number of pips, Y = number of pips on E ( XY ) = E ( X ) E ( Y ) = 0 . � � = ∑ ∑ xyP [ X = x ] P [ Y = y ] die 1 minus number on die 2. X and Y are not independent. x y Indeed: P [ X = 12 , Y = 1 ] = 0 � = P [ X = 12 ] P [ Y = 1 ] > 0. Hence, = ∑ � � �� ∑ xP [ X = x ] yP [ Y = y ] x y E (( X + Y ) 2 ) = E ( X 2 + 2 XY + Y 2 ) var ( X + Y ) = = ∑ xP [ X = x ] E [ Y ] = E [ X ] E [ Y ] . E ( X 2 )+ 2 E ( XY )+ E ( Y 2 ) = E ( X 2 )+ E ( Y 2 ) = x = var ( X )+ var ( Y ) . Examples. Variance: binomial. Variance of Binomial Distribution. Flip coin with heads probability p . (1) Assume that X , Y , Z are (pairwise) independent, with X - how many heads? E [ X ] = E [ Y ] = E [ Z ] = 0 and E [ X 2 ] = E [ Y 2 ] = E [ Z 2 ] = 1. � 1 Then if i th flip is heads X i = 0 otherwise n � n � E [( X + 2 Y + 3 Z ) 2 ] E [ X 2 ] ∑ i 2 p i ( 1 − p ) n − i . = i = E [ X 2 + 4 Y 2 + 9 Z 2 + 4 XY + 12 YZ + 6 XZ ] i ) = 1 2 × p + 0 2 × ( 1 − p ) = p . i = 0 E ( X 2 = Really???!!##... Var ( X i ) = p − ( E ( X )) 2 = p − p 2 = p ( 1 − p ) . = 1 + 4 + 9 + 4 × 0 + 12 × 0 + 6 × 0 p = 0 = ⇒ Var ( X i ) = 0 = 14 . Too hard! p = 1 = ⇒ Var ( X i ) = 0 Ok.. fine. (2) Let X , Y be independent and U { 1 , 2 ,..., n } . Then X = X 1 + X 2 + ... X n . Let’s do something else. E [ X 2 + Y 2 − 2 XY ] = 2 E [ X 2 ] − 2 E [ X ] 2 E [( X − Y ) 2 ] Maybe not much easier...but there is a payoff. = X i and X j are independent: Pr [ X i = 1 | X j = 1 ] = Pr [ X i = 1 ] . 1 + 3 n + 2 n 2 − ( n + 1 ) 2 = . Var ( X ) = Var ( X 1 + ··· X n ) = np ( 1 − p ) . 3 2
Conditioning of RVs Conditional distributions Revisiting mean of geometric RV X ∼ G ( p ) X | Y is a RV: X is memoryless Recall conditioning on an event A p XY ( x , y ) p X | Y ( x | y ) = ∑ ∑ = 1 P [ X = n + m | X > n ] = P [ X = m ] . p Y ( y ) P [ X = k | A ] = P [( X = k ) ∩ A ] x x P [ A ] Multiplication or Product Rule: Thus E [ X | X > 1 ] = 1 + E [ X ] . Conditioning on another RV p XY ( x , y ) = p X ( x ) p Y | X ( y | x ) = p Y ( y ) p X | Y ( x | y ) Why? (Recall E [ g ( X )] = ∑ l g ( l ) P [ X = l ] ) P [ X = k | Y = m ] = P [ X = k , Y = m ] ∞ Total Probability Theorem: If A 1 , A 2 , ... , A N partition Ω , and = p X | Y ( x | y ) ∑ P [ Y = m ] E [ X | X > 1 ] = kP [ X = k | X > 1 ] P [ A i ] > 0 ∀ i , then k = 1 N ∞ p X | Y ( x | y ) is called the conditional distribution or ∑ p X ( x ) = P [ A i ] P [ X = x | A i ] ∑ = kP [ X = k − 1 ] ( memoryless ) conditional probability mass function (pmf) of X given Y i = 1 k = 2 ∞ Nothing special about just two random variables, naturally ∑ = ( l + 1 ) P [ X = l ] ( l = k − 1 ) p X | Y ( x | y ) = p XY ( x , y ) extends to more. l = 1 p Y ( y ) = E [ X + 1 ] = 1 + E [ X ] Let’s visit the mean and variance of the geometric distribution using conditional expectation. Revisiting mean of geometric RV X ∼ G ( p ) Summary of Conditional distribution Summary. X is memoryless For Random Variables X and Y , P [ X = x | Y = k ] is the conditional distribution of X given Y = k Joint and Conditional Distributions. P [ X = k + m | X > k ] = P [ X = m ] . Thus E [ X | X > 1 ] = 1 + E [ X ] . Joint distributions: P [ X = x | Y = k ] = P [ X = x , Y = k ] ◮ Normalization: ∑ x , y P [ X = x , Y = y ] = 1. We have E [ X ] = P [ X = 1 ] E [ X | X = 1 ]+ P [ X > 1 ] E [ X | X > 1 ] . P [ Y = k ] ◮ Marginalization: ∑ y P [ X = x , Y = y ] = P [ X = x ] . ⇒ E [ X ]= p . 1 +( 1 − p )( E [ X ]+ 1 ) Numerator: Joint distribution of ( X , Y ) . ◮ Independence: P [ X = x , Y = y ] = P [ X = x ] P [ Y = y ] for all ⇒ E [ X ] = p + 1 − p + E [ X ] − pE [ X ] Denominator: Marginal distribution of Y . x , y . E [ XY ] = E [ X ] E [ Y ] . ⇒ pE [ X ] = 1 Conditional distributions: (Aside: surprising result using conditioning of RVs): ⇒ E [ X ] = 1 ◮ Sum of independent Poissons is Poisson. Theorem : If X ∼ Poisson( λ 1 ) , Y ∼ Poisson( λ 2 ) are independent, p ◮ Conditional expectation: useful for mean & variance then X + Y ∼ Poisson( λ 1 + λ 2 ) . calculations Derive the variance for X ∼ G ( p ) by finding E [ X 2 ] using “Sum of independent Poissons is Poisson.” conditioning.
Recommend
More recommend