Dynamic Programming Part I Lecture 6 September 12, 2013 Maximum - PowerPoint PPT Presentation

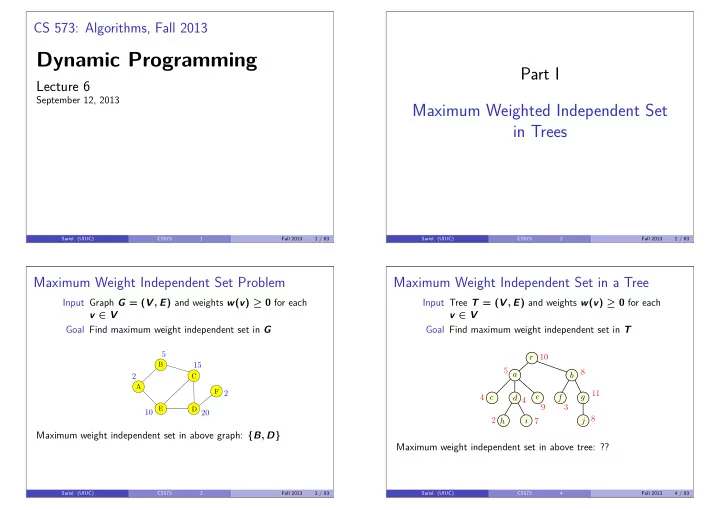
CS 573: Algorithms, Fall 2013 Dynamic Programming Part I Lecture 6 September 12, 2013 Maximum Weighted Independent Set in Trees Sariel (UIUC) CS573 1 Fall 2013 1 / 83 Sariel (UIUC) CS573 2 Fall 2013 2 / 83 Maximum Weight Independent Set Problem Maximum Weight Independent Set in a Tree Input Graph G = ( V , E ) and weights w ( v ) ≥ 0 for each Input Tree T = ( V , E ) and weights w ( v ) ≥ 0 for each v ∈ V v ∈ V Goal Find maximum weight independent set in G Goal Find maximum weight independent set in T 5 10 r B 15 5 8 a b 2 C A F 2 11 e g 4 c d f 4 9 3 E D 10 20 8 2 i j h 7 Maximum weight independent set in above graph: { B , D } Maximum weight independent set in above tree: ?? Sariel (UIUC) CS573 3 Fall 2013 3 / 83 Sariel (UIUC) CS573 4 Fall 2013 4 / 83

Towards a Recursive Solution Towards a Recursive Solution For an arbitrary graph G : Natural candidate for v n is root r of T ? Let O be an optimum solution to the whole problem. Number vertices as v 1 , v 2 , . . . , v n 1 Case r �∈ O : Then O contains an optimum solution for each Find recursively optimum solutions without v n (recurse on 2 subtree of T hanging at a child of r . G − v n ) and with v n (recurse on G − v n − N ( v n ) & include v n ). Case r ∈ O : None of the children of r can be in O . O − { r } Saw that if graph G is arbitrary there was no good ordering that 3 contains an optimum solution for each subtree of T resulted in a small number of subproblems. hanging at a grandchild of r . Subproblems? Subtrees of T hanging at nodes in T . What about a tree? Natural candidate for v n is root r of T ? Sariel (UIUC) CS573 5 Fall 2013 5 / 83 Sariel (UIUC) CS573 6 Fall 2013 6 / 83 A Recursive Solution Iterative Algorithm T ( u ) : subtree of T hanging at node u Compute OPT ( u ) bottom up. To evaluate OPT ( u ) need to 1 OPT ( u ) : max weighted independent set value in T ( u ) have computed values of all children and grandchildren of u What is an ordering of nodes of a tree T to achieve above? 2 Post-order traversal of a tree.  � v child of u OPT ( v ) ,  OPT ( u ) = max w ( u ) + � v grandchild of u OPT ( v )  Sariel (UIUC) CS573 7 Fall 2013 7 / 83 Sariel (UIUC) CS573 8 Fall 2013 8 / 83

Iterative Algorithm Example 10 r MIS-Tree ( T ): Let v 1 , v 2 , . . . , v n be a post-order traversal of nodes of T 5 for i = 1 to n do 8 a b � � � v j child of v i M [ v j ] , M [ v i ] = max w ( v i ) + � v j grandchild of v i M [ v j ] 11 return M [ v n ] (* Note: e g v n is the root of T *) 4 c d f 4 9 3 Space: O ( n ) to store the value at each node of T 8 2 i j Running time: h 7 Naive bound: O ( n 2 ) since each M [ v i ] evaluation may take 1 O ( n ) time and there are n evaluations. Better bound: O ( n ) . A value M [ v j ] is accessed only by its 2 parent and grand parent. Sariel (UIUC) CS573 9 Fall 2013 9 / 83 Sariel (UIUC) CS573 10 Fall 2013 10 / 83 Dominating set Definition G = ( V , E ) . The set X ⊆ V is a dominating set , if any vertex Part II v ∈ V is either in X or is adjacent to a vertex in X . 10 r Problem DAGs and Dynamic Programming 5 Given weights on 8 a b vertices, compute the minimum weight 11 e g dominating set in G . 4 c d f 4 9 3 is Dominating Set 8 NP-Hard ! 2 j h i 7 Sariel (UIUC) CS573 11 Fall 2013 11 / 83 Sariel (UIUC) CS573 12 Fall 2013 12 / 83

Recursion and DAG s Iterative Algorithm for... Dynamic Programming and DAG s Observation Observation Let A be a recursive algorithm for problem Π . For each instance I of An iterative algorithm B obtained from a recursive algorithm A for a Π there is an associated DAG G ( I ) . problem Π does the following: For each instance I of Π , it computes a topological sort Create directed graph G ( I ) as follows... 1 of G ( I ) and evaluates sub-problems according to the For each sub-problem in the execution of A on I create a node. 2 topological ordering. If sub-problem v depends on or recursively calls sub-problem u 3 add directed edge ( u , v ) to graph. Sometimes the DAG G ( I ) can be obtained directly without 1 G ( I ) is a DAG . Why? If G ( I ) has a cycle then A will not thinking about the recursive algorithm A 4 terminate on I . In some cases (not all) the computation of an optimal solution 2 reduces to a shortest/longest path in DAG G ( I ) Topological sort based shortest/longest path computation is 3 dynamic programming! Sariel (UIUC) CS573 13 Fall 2013 13 / 83 Sariel (UIUC) CS573 14 Fall 2013 14 / 83 A quick reminder... Weighted Interval Scheduling via... A Recursive Algorithm for weighted interval scheduling Longest Path in a DAG Let O i be value of an optimal schedule for the first i jobs. Given intervals, create a DAG as follows: Schedule ( n ): Create one node for each interval, plus a dummy sink node 0 for if n = 0 then return 0 1 if n = 1 then return w ( v 1 ) interval 0 , plus a dummy source node s . O p ( n ) ← Schedule ( p ( n ) ) For each interval i add edge ( i , p ( i )) of the length/weight of v i . 2 O n − 1 ← Schedule ( n − 1 ) Add an edge from s to n of length 0 . if ( O p ( n ) + w ( v n ) < O n − 1 ) then 3 O n = O n − 1 For each interval i add edge ( i , i − 1 ) of length 0 . 4 else O n = O p ( n ) + w ( v n ) return O n Sariel (UIUC) CS573 15 Fall 2013 15 / 83 Sariel (UIUC) CS573 16 Fall 2013 16 / 83

Example Relating Optimum Solution Given interval 70 3 problem instance I let G ( I ) denote the DAG constructed as described. 30 80 4 1 5 2 10 20 p (5) = 2, p (4) = 1, p (3) = 1, p (2) = 0, p (1) = 0 Claim Optimum solution to weighted interval scheduling instance I is given 4 by longest path from s to 0 in G ( I ) . 3 70 80 30 s 1 0 Assuming claim is true, 2 20 If I has n intervals, DAG G ( I ) has n + 2 nodes and O ( n ) 5 1 10 edges. Creating G ( I ) takes O ( n log n ) time: to find p ( i ) for each i . How? Longest path can be computed in O ( n ) time — recall 2 O ( m + n ) algorithm for shortest/longest paths in DAG s. Sariel (UIUC) CS573 17 Fall 2013 17 / 83 Sariel (UIUC) CS573 18 Fall 2013 18 / 83 DAG for Longest Increasing Sequence Given sequence a 1 , a 2 , . . . , a n create DAG as follows: add sentinel a 0 to sequence where a 0 is less than smallest 1 Part III element in sequence for each i there is a node v i 2 if i < j and a i < a j add an edge ( v i , v j ) 3 Edit Distance and Sequence find longest path from v 0 4 Alignment a 0 6 5 7 1 3 2 8 a 0 6 3 5 2 7 8 1 Sariel (UIUC) CS573 19 Fall 2013 19 / 83 Sariel (UIUC) CS573 20 Fall 2013 20 / 83

Spell Checking Problem Edit Distance Given a string “exponen” that is not in the dictionary, how should a Definition spell checker suggest a nearby string? Edit distance between two words X and Y is the number of letter insertions, letter deletions and letter substitutions required to obtain Y from X . What does nearness mean? Example The edit distance between FOOD and MONEY is at most 4 : Question: Given two strings x 1 x 2 . . . x n and y 1 y 2 . . . y m what is a distance between them? FOOD → MOOD → MONOD → MONED → MONEY Edit Distance: minimum number of “edits” to transform x into y . Sariel (UIUC) CS573 21 Fall 2013 21 / 83 Sariel (UIUC) CS573 22 Fall 2013 22 / 83 Edit Distance: Alternate View Edit Distance Problem Alignment Problem Given two words, find the edit distance between them, i.e., an Place words one on top of the other, with gaps in the first word alignment of smallest cost. indicating insertions, and gaps in the second word indicating deletions. F O O D M O N E Y Formally, an alignment is a set M of pairs ( i , j ) such that each index appears at most once, and there is no “crossing”: i < i ′ and i is matched to j implies i ′ is matched to j ′ > j . In the above example, this is M = { ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) , ( 4 , 5 ) } . Cost of an alignment is the number of mismatched columns plus number of unmatched indices in both strings. Sariel (UIUC) CS573 23 Fall 2013 23 / 83 Sariel (UIUC) CS573 24 Fall 2013 24 / 83

Applications Similarity Metric Spell-checkers and Dictionaries 1 Definition Unix diff 2 For two strings X and Y , the cost of alignment M is DNA sequence alignment . . . but, we need a new metric 3 [Gap penalty] For each gap in the alignment, we incur a cost δ . 1 [Mismatch cost] For each pair p and q that have been matched 2 in M , we incur cost α pq ; typically α pp = 0 . Edit distance is special case when δ = α pq = 1 . Sariel (UIUC) CS573 25 Fall 2013 25 / 83 Sariel (UIUC) CS573 26 Fall 2013 26 / 83 An Example Sequence Alignment Input Given two words X and Y , and gap penalty δ and Example mismatch costs α pq o c u r r a n c e Goal Find alignment of minimum cost o c c u r r e n c e Cost = δ + α ae Alternative: o c u r r a n c e o c c u r r e n c e Cost = 3 δ Or a really stupid solution (delete string, insert other string): o c u r r a n c e o c c u r r e n c e Cost = 19 δ . Sariel (UIUC) CS573 27 Fall 2013 27 / 83 Sariel (UIUC) CS573 28 Fall 2013 28 / 83