Decoders and Trees 2 n 1 2 n 1 AND (2 n 1 ) AND (2 n 1 ) y [2 n - PowerPoint PPT Presentation

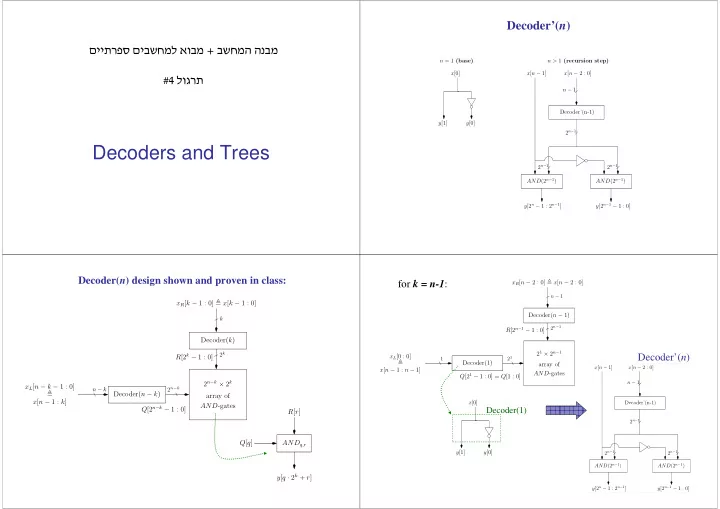
Decoder’( n ) �������������������� �� ����������� n = 1 (base) n > 1 (recursion step) x [0] x [ n − 1] x [ n − 2 : 0] ��� � ������ n − 1 Decoder’(n-1) y [1] y [0] 2 n − 1 Decoders and Trees 2 n − 1 2 n − 1 AND (2 n − 1 ) AND (2 n − 1 ) y [2 n − 1 : 2 n − 1 ] y [2 n − 1 − 1 : 0] Decoder( n ) design shown and proven in class: for k = n-1 : x R [ n − 2 : 0] � x [ n − 2 : 0] n − 1 x R [ k − 1 : 0] � x [ k − 1 : 0] Decoder( n − 1) k 2 n − 1 R [2 n − 1 − 1 : 0] Decoder( k ) 2 1 × 2 n − 1 Decoder’( n ) 2 k R [2 k − 1 : 0] x L [0 : 0] 2 1 1 � Decoder(1) array of x [ n − 1] x [ n − 2 : 0] x [ n − 1 : n − 1] AND -gates Q [2 1 − 1 : 0] = Q [1 : 0] 2 n − k × 2 k n − 1 x L [ n − k − 1 : 0] 2 n − k n − k � Decoder( n − k ) array of x [ n − 1 : k ] x [0] Decoder’(n-1) AND -gates Q [2 n − k − 1 : 0] Decoder(1) R [ r ] 2 n − 1 Q [ q ] AND q,r y [1] y [0] 2 n − 1 2 n − 1 AND (2 n − 1 ) AND (2 n − 1 ) y [ q · 2 k + r ] y [2 n − 1 : 2 n − 1 ] y [2 n − 1 − 1 : 0]

Decoder’( n ) is a private case of Decoder( n ) design. ( k = n-1 or k = 1 ) Delay analysis: � � � � d INV if n 1 Decoder’( n ) is a correct implementation of a decoder. � d n � ( ) � � � � � � � � d INV d n � � d AND � max , 1 otherwise Cost analysis: � � � � c INV if n 1 Solving the recurrence: � � � c n � � � � � � c n � � � n � c AND � c INV 1 � � � � � � � � � � � ( 1 ) 2 2 otherwise � � � � d n d INV d n d AND n 1 : max , 1 Solving the recurrence: � � � � � d n � � d AND 1 � � � � � � � � � � � � n � � n c n c n c AND c INV 1 : 1 2 � � � � � � � � � � � � � � � � � � n � n � � � � � � � � d � n � d AND c c AND n c INV 1 2 1 2 2 � 2 1 1 1 n � � 1 2 1 � � � � � � � � � � � � � � n � c INV � � c AND d INV n d AND 2 2 1 � 2 1 � � � � � � � � � � n � c INV � n � � c AND � � 1 n 2 4 asymptotics Linear Delay!!! � � � � n 2 Decoder( n ) for k = n/2 Consider the top two recursion steps: x [ n − 1 : n/ 2] x [ n/ 2 − 1 : 0] each AND-gate in the “AND-gates array” of the second recursion step, i.e. Decoder( n/2 ), feeds 2 n/2 AND-gates in the “AND-gates array” of the primary recursion step, i.e. Decoder( n ). Decoder(n/2) Decoder(n/2) B [2 n/ 2 − 1 : 0] A [2 n/ 2 − 1 : 0] n � Maximum fanout of a net 2 2 B [ ⌊ i/ 2 n/ 2 ⌋ ] A [ i mod 2 n/ 2 ] � � � � � c INV � if n 1 � � n � � 2 AND � c n � � � � � � � n � c c AND n � 2 2 otherwise 2 ( i ∈ { 0 , 1 , . . ., 2 n − 1 } ) Y [ i ] � � � � � � � � � � � � I x n n 1 1 : 0 1 : 0 n � A i � 2 2 mod , 2 2 � � � 0 otherwise � d INV � if n 1 � � d n � � � n � ( ) log � � � � � d d AND n � otherwise � � � � � � � � � � I n x n � i � n n 2 1 1 : 1 : � � � B � 2 2 � � n � � � � � 0 otherwise 2 2

Design Decoder(n) Decoder’(n) Balanced Trees n k=n/2 � � 0 if n 1 1 1 1 � � � d n OR � � � � � d � d OR n Cost � otherwise 2 10 10 2 4 52 60 OR-Tree( n/2 ) OR-Tree( n/2 ) 8 616 1024 � � � � � � � � d n n d OR log n n 2 2 2 16 132304 262152 Logarithmic Delay Lower Bound Theorem: Design Decoder(n) Decoder’(n) Let C = < G , N > denote a combinational circuit that implements a non-constant Boolean function f : {0,1} n � {0,1}. n k=n/2 If the fan-in of every gate in G is at most c, then the delay of C is at least 1 1 1 log c |cone( f )|. � � 2 Delay � � 4 cone(OR n ) = n Delay of the balanced 8 7 15 delay(OR n ) � log 2 ( n )·d(OR) tree is minimized. fan-in � 2 16 9 31 Recursive algorithm for computing an OR-tree( n ) Proof: We first show that for every n > 2 there exist a pair of positive numbers a , b such that: � � a b n (i) 1. The case that n � 2 is trivial. � � � � � a � � b � � n � 1 (ii) max log , log log 2 2 2 2. If n > 2, then let a , b be any pair of positive integers such that n (i) n = a + b and (ii) max{ � log 2 a � , � log 2 b � } � � log 2 n � - 1. � � � k � n � k a b 1 there exists one such pair : 2 if 2 2 3. Compute an OR-tree( a ) and an OR-tree( b ). � � � � � a � � b � � n � 1 obviously, max log , log log Connect their outputs to an OR-gate to obtain an OR-tree( n ). 2 2 2 � k k � 1 1 � � k � Claim: the above algorithm computes a minimum delay OR-tree. n � k � a � k 1 a � � k if 2 2 set : 2 log 2 b � n � 2 � k k � � b � � k 2 log Note that this is the most 2 unbalanced partition of n, and � k � � n � log 2 1 still we get the minimal delay.

We prove by induction on n that the delay of the computed OR-tree is Buffers � log 2 n � ·d(OR) to obtain delay minimality. � � � buffer � c 1 1 � ! buffer 1 n = 1 or n = 2 are trivial cases. Induction basis: � � � buffer � d 1 1 � � � � � � � � � � � k n d OR tree k � k � d OR Induction hypothesis: . log fanout � 2 2 Induction step: we prove the claim for n , A balanced tree structure minimizes the delay and cost. The tree is a binary tree due to fan-out limitations. � � � � � � � � � � � � � � � � d OR � tree n � d OR � tree a d OR � tree b � d OR max , Notice: * The leaves of the tree feed the gate outputs. � � � � � � � induction hypothesis � � a � � b � � d OR � d OR max log , log * The root of the tree is fed by the gate input. 2 2 * The first branching is free � no need for a “root” gate. � � � � � � � � � � � n � d OR d OR log 2 1 � � � � � � � � � � d n � n � d buffer log 2 1 1 � � � n � � � d OR log � � � � � � 2 � � � � c n n c buffer 2 1 x [ n − 1] x [ n − 2 : 0] Fanout limitation effect on design Delay analysis: n − 1 fanout � 2 n � 1 : x [ n − 1] x [ n − 2 : 0] Decoder’(n-1) � � � � � d d INV Cost analysis: 1 n − 1 � n 2 n − 1 1 : 1-buf-trees � n 1 : � � � � Decoder’(n-1) � � � � � � � c c INV � � � � n � % d INV d buf tree 1 1 1 2 " � � � � " � � � � � 2 n − 1 d n � d � buf � d � buf � tree n 1 2 n − 1 2 n − 1 � $ 1-buf-trees max 1 1 2 � n 1 : " " � � � AND (2 n − 1 ) AND (2 n − 1 ) d n 1 � # � � � � � � � � � � � n � � c n c n c AND c INV 1 2 � � � d AND 2 n − 1 2 n − 1 � � � � � � y [2 n − 1 : 2 n − 1 ] y [2 n − 1 − 1 : 0] � � � � n � � � c buf tree c buf 1 2 1 2 1 AND (2 n − 1 ) AND (2 n − 1 ) � � � � � � d INV � n � � d � buf � % 1 1 � � � � � � � � � n � � c n c AND c INV " " 1 2 � � y [2 n − 1 : 2 n − 1 ] y [2 n − 1 − 1 : 0] � � � n d buf � $ max 1 � � � � � n � � c � buf " " 2 3 1 � � � d n � 1 # � � � d AND