
Control with binary code William Sandqvist william@kth.se
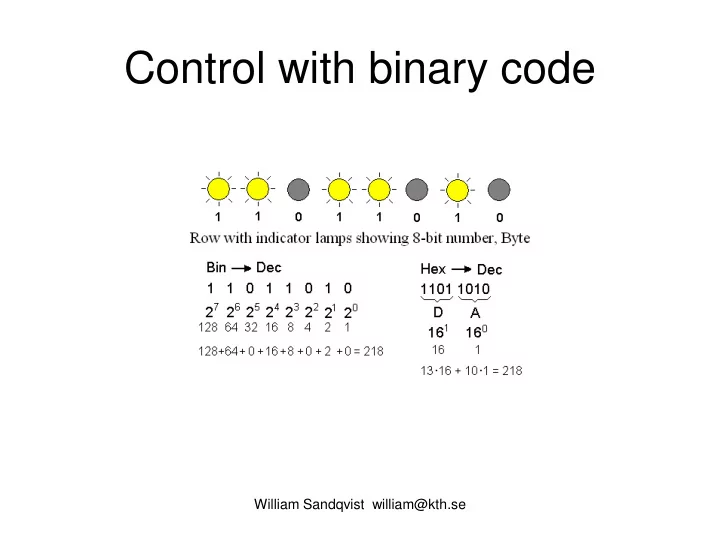
Dec – Bin – Hex – Oct 218 10 = 11011010 2 = DA 16 = 332 8 William Sandqvist william@kth.se
Ex 1.1c Decimal to Binäry binary weights: 1024 512 256 128 64 32 16 8 4 2 1 71 10 = ? 2 William Sandqvist william@kth.se
Ex 1.1c Decimal to Binäry binary weights: 1024 512 256 128 64 32 16 8 4 2 1 71 10 = ? 2 71 10 = (64+7= 64+4+2+1) =1000111 2 William Sandqvist william@kth.se
Ex. 1.2a Binary to Decimal binary weights: 1024 512 256 128 64 32 16 8 4 2 1 101101001 2 = ? 10 William Sandqvist william@kth.se
Ex. 1.2a Binary to Decimal binary weights: 1024 512 256 128 64 32 16 8 4 2 1 101101001 2 = ? 10 101101001 2 = (2 8 +2 6 +2 5 +2 3 +2 0 =256+64+32+8+1) =361 10 William Sandqvist william@kth.se
Ex 1.3c Binary/Octal/Hexadecimal 100110101 2 = ? 16 = ? 8 William Sandqvist william@kth.se
Ex 1.3c Binary/Octal/Hexadecimal 100110101 2 = ? 16 = ? 8 1 0011 0101 2 = 1 3 5 16 William Sandqvist william@kth.se
Ex 1.3c Binary/Octal/Hexadecimal 100110101 2 = ? 16 = ? 8 1 0011 0101 2 = 1 3 5 16 100 110 101 2 = 4 6 5 8 William Sandqvist william@kth.se
Venn-diagram x in common with y x together with y x in common with outside y William Sandqvist william@kth.se
Ex. 3.2 De Morgans theorem with Venn diagram Prove De Morgans theorem with the use of Venn Diagram. William Sandqvist william@kth.se
Ex. 3.2 De Morgan William Sandqvist william@kth.se
Ex. 3.2 De Morgan William Sandqvist william@kth.se
Ex. 3.2 De Morgan = William Sandqvist william@kth.se
Ex. 3.2 De Morgan = William Sandqvist william@kth.se
Ex. 3.2 De Morgan = Now proved! William Sandqvist william@kth.se
(Ex. 5.1) How to open the code-lock? (=minterm) Which buttons should be simultaneously pressed in order to light up the lamp? ( = open up the lock) William Sandqvist william@kth.se
(Ex. 5.1) How to open the code-lock? (=minterm) Which buttons should be simultaneously pressed in order to light up the lamp? ( = open up the lock) Answer: 4,d and 2,h but you must simultaneously avoid pressing a b c e f g i and k ! William Sandqvist william@kth.se
(Ex. 5.1) How to open the code-lock? (=minterm) Which buttons should be simultaneously pressed in order to light up the lamp? ( = open up the lock) Answer: 4,d and 2,h but you must simultaneously avoid pressing a b c e f g i and k ! William Sandqvist william@kth.se
(Ex. 5.1) How to open the code-lock? (=minterm) Which buttons should be simultaneously pressed in order to light up the lamp? ( = open up the lock) Answer: 4,d and 2,h but you must simultaneously avoid pressing a b c e f g i and k ! A product-term with all variables is called a minterm . William Sandqvist william@kth.se
Ex 3.3 Venn Diagram a) Draw a Venn Diagram for thre variables and mark all truth table minterms in the diagram. b) Minimize this function with the help of the Venn Diagram. = + + + + f x x x x x x x x x x x x x x x 2 1 2 1 0 0 1 0 2 0 2 1 2 1 0 William Sandqvist william@kth.se
Ex. 3.3a Truth Table – Venn diagram William Sandqvist william@kth.se
Ex. 3.3b simplified expression Orginal expression. William Sandqvist william@kth.se
Ex. 3.3b simplified expression Orginal expression. Simplified! William Sandqvist william@kth.se
Boole’s algebra rules Logical addition "+", OR , and logical multiplication "×", AND , broadly follows the usual normal algebraic distributive, commutative and associative laws (with one exception). William Sandqvist william@kth.se
Theorems Rules William Sandqvist william@kth.se
Ex. 4.1(a, b, c, h) Boolean algebra William Sandqvist william@kth.se
Ex. 4.1a = = ⋅ ⋅ ⋅ ⋅ + + ⋅ ⋅ = = ⋅ ⋅ + = ⋅ f f a a c c d d a a d d { factor ad } a d ( c 1 ) a d William Sandqvist william@kth.se
Ex. 4.1b = ⋅ + ⋅ + ⋅ = ⋅ + ⋅ ⋅ + ⋅ ⋅ = f a ( b a c a b ) a b a a c a a b = + + ⋅ = ⋅ + = a b 0 a b a ( b b ) a William Sandqvist william@kth.se
Ex. 4.1c = + + ⋅ + = f a b a b c William Sandqvist william@kth.se
Ex. 4.1c = + + ⋅ + = + + ⋅ + ⋅ + = f a b a b c a ( a a ) b a b c = + ⋅ + ⋅ + ⋅ + = a a b a b a b c = + ⋅ + ⋅ + + = a a b a ( b b ) c = + = ... a a ... 1 William Sandqvist william@kth.se
Ex. 4.1h = + ⋅ = f a ( a b ) William Sandqvist william@kth.se
Ex. 4.1h = + ⋅ = = + + = + f a ( a b ) { deMorgan } a a b a b William Sandqvist william@kth.se
Ex. 4.4 De Morgan William Sandqvist william@kth.se
Ex. 4.4 + + + + + + = + + + + + + + = ( a b c )( a b c )( a b c b c ) ( a b c )( a b c )( a b c b c ) = + + + + + + = ( a b c )( a b c )( a b c ) + + + + + + + + = + + = + + + = ( ) ( ) ( ) a b c a b c a b c a b c a bc a b c a b c a b c a bc a b c = + + + = + a c ( b b ) b c ( a a ) a c b c Duplicate! William Sandqvist william@kth.se
Logic gates William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. AND 0 William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. AND OR 0 1 William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. AND OR XOR 0 1 0 William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. AND OR XOR 0 1 0 NAND 0 William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. AND OR XOR 0 1 0 NAND NOR 0 1 William Sandqvist william@kth.se
(Ex. 4.5a) Gates Enter the name and output 1/0 for the following six gate types when the input signals are as shown in the figure. AND OR XOR 0 1 0 XNOR NAND NOR 0 1 1 William Sandqvist william@kth.se
Ex. 4.7 Timing diagram and Truth Table William Sandqvist william@kth.se
Ex. 4.7 William Sandqvist william@kth.se
Ex. 4.7 William Sandqvist william@kth.se
Ex. 4.7 William Sandqvist william@kth.se
Ex. 4.7 William Sandqvist william@kth.se
Ex. 4.12 From text to Boolean equations A combinatorical circuit with six input signals x 5 , x 4 , x 3 , x 2 , x 1 and three output signals u 2 , u 1 , u 0 , is described in this way: • u 0 = 1 if and only if ”either both x 0 and x 2 are 0 or x 4 and x 5 are different” • u 1 = 1 if and only if ”x 0 and x 1 are equal and x 5 is the inverse of x 2 ” • u 2 = 0 if and only if ”x 0 is 1 and some of x 1 … x 5 is 0” William Sandqvist william@kth.se
ÖH 4.12 AND u 0 = 1 if and only if ” either both x 0 and x 2 are 0 NOT XOR or x 4 and x 5 are different” XOR = ⋅ ⊕ ⊕ u x x ( x x ) 2 0 0 4 5 William Sandqvist william@kth.se
ÖH 4.12 u 1 = 1 if and only if ” x 0 and x 1 are equal and x 5 is the inverse of x 2 ” AND XOR XNOR = ⊕ ⋅ ⊕ u x x ( x x ) 1 0 1 5 2 = + ⋅ + ( x x x x ) ( x x x x ) 0 1 5 2 0 1 2 5 William Sandqvist william@kth.se
ÖH 4.12 NOT u 2 = 0 if and only if ” x 0 is 1 and some of x 1 … x 5 is 0 ” NOT OR AND = ⋅ + + + + u x ( x x x x x ) 3 4 5 0 1 2 2 ⇒ = ⋅ + + + + = u x ( x x x x x ) 1 2 3 4 5 2 0 = + + + + + = x ( x x x x x ) 3 0 1 2 4 5 = + ⋅ ⋅ ⋅ ⋅ x x x x x x 0 1 2 3 4 5 William Sandqvist william@kth.se
Logic circuits of SoP-form All the logical functions can be realized by using gate types AND and OR combined in two steps. We assume here that the input variables are also available in inverted form, if not then you of course inverters too. One can realize the gate circuit AND-OR logic, SoP-form direct from the truth table. Each "1" in the table is a minterm. The function is the sum of these minterms. One says that the function is expressed in the SoP form (Sum of Products). However, there may exist a simpler circuit with fewer gates that do the same job. William Sandqvist william@kth.se
Ex. 5.2 SoP and PoS normal form A locic function has this Truth Table: Write the function on SoP normal form: Write the function on PoS normal form: William Sandqvist william@kth.se
Ex. 5.2 SoP-form A logical function has the following truth table. Specify the function of SoP-normal form (sum of products). William Sandqvist william@kth.se
Recommend
More recommend