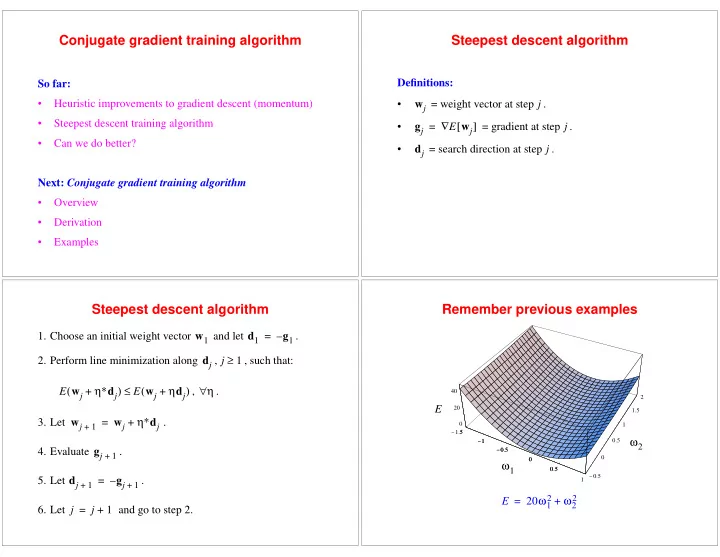

Conjugate gradient training algorithm Steepest descent algorithm Definitions: So far: j • Heuristic improvements to gradient descent (momentum) • w j = weight vector at step . • Steepest descent training algorithm ∇ [ ] E w j j • = = gradient at step . g j • Can we do better? j • = search direction at step . d j Next: Conjugate gradient training algorithm • Overview • Derivation • Examples Steepest descent algorithm Remember previous examples 1. Choose an initial weight vector w 1 and let d 1 = – g 1 . ≥ j 2. Perform line minimization along d j , 1 , such that: η∗ d j ( ) ≤ ( η d j ) ∀ η E w j E w j + + , . 40 2 E 20 1.5 η∗ d j 3. Let w j = w j + . 0 1 + 1 - 1.5 1.5 ω 2 - 1 - 1 0.5 - 0.5 - 0.5 4. Evaluate g j . + 1 0 0 0 ω 1 0.5 0.5 - 0.5 5. Let d j = – g j . 1 + 1 + 1 20 ω 1 ω 2 E 2 2 = + j j 6. Let = + 1 and go to step 2.
Remember previous examples Steepest descent algorithm examples 2 2 1.5 1.5 1 ω 2 ω 2 1 1 0.75 2 0.5 1 0.25 0.5 0.5 0 ω 2 - 2 - 2 0 - 1 - 1 0 - 1 0 0 0 - 1 - 0.5 ω 1 0 0.5 1 ω 1 - 1 - 0.5 ω 1 0 0.5 1 1 1 - 2 steepest descent steepest descent 2 15 steps to convergence 24 steps to convergence E ω 1 ω 2 ( , ) ( 5 ω 1 ω 2 ) 2 2 = 1 – exp – – quadratic non-quadratic Conjugate gradient algorithm (a sneak peek) Conjugate gradient algorithm (sneak peak) 1. Choose an initial weight vector w 1 and let d 1 = – g 1 . 2 2 2. Perform a line minimization along , such that: d j 1.5 1.5 η∗ d j ( ) ≤ ( η d j ) ∀ η E w j E w j + + , . ω 2 ω 2 1 1 η∗ d j 3. Let = + . w j w j + 1 4. Evaluate . 0.5 g j 0.5 + 1 β j d j 5. Let d j = – g j + where, + 1 + 1 0 0 - 1 - 0.5 ω 1 ω 1 0 0.5 1 - 1 - 0.5 0 0.5 1 T ( ) g j g j – g j + 1 + 1 β j = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - conjugate gradient conjugate gradient T g j g j 5 steps to convergence 2 steps to convergence j j quadratic non-quadratic 6. Let = + 1 and go to step 2.
SD vs . CG Conjugate gradients: a first look In steepest descent: ] T d t g w t [ ( ) ( ) Key difference: new search direction + 1 = 0 • Very little additional computation (over steepest descent). (What does this mean?) • No more oscillation back and forth. Key question: • Why/How does this improve things? Knowledge of local quadratic properties of error surface... Conjugate gradients: a first look How do we achieve non-interfering directions? Non-interfering directions: FACT: ] T d t g w t [ ( ) η d t ( ) ( ) η ≥ + 1 + + 1 = 0 , 0 ] T d t g w t [ ( ) η d t ( ) ( ) , η ≥ + 1 + + 1 = 0 0 (What the #$@!# does this mean?) implies ) T Hd t ( ( ) d t (H-orthogonality, conjugacy) + 1 = 0 Hmmm ... need to pay attention to 2nd-order properties of error surface... 1 b T w - w T Hw E w ( ) E 0 = + + - - 2
Show H-orthogonality requirement Show H-orthogonality requirement ( ) Approximate g w by 1st-order Taylor approximation [ ( ) η d t ( ) ] T [ ( ) ] T η d t ( ) T H g w t g w t + 1 + + 1 = + 1 + + 1 about w 0 : ( ) d t Post-multiply by : ) T ) T ) T ( ≈ ( ( ∇ { ( ) } g w g w 0 + w – w 0 g w 0 • Left-hand side: ] T d t [ ( ) η d t ( ) ( ) g w t + 1 + + 1 = 0 (assumption) w t ( ) = + 1 Let w 0 : • Right-hand side: ) T ] T ] T ( g w t [ ( ) [ w t ( ) ∇ { g w t [ ( ) ] } = + 1 + – + 1 + 1 g w w ] T d t ) T Hd t [ ( ) ( ) η d t ( ( ) g w t + 1 + + 1 = 0 ) T Hd t η d t ( ( ) ( ) w t ( ) η d t ( ) + 1 = 0 = + 1 + + 1 Evaluate g w at w : ] T ] T ) T H ) T Hd t g w t [ ( ) η d t ( ) g w t [ ( ) η d t ( d t ( ( ) + 1 + + 1 = + 1 + + 1 + 1 = 0 (implication) How do we achieve non-interfering Derivation of conjugate gradient algorithm directions? • Local quadratic assumption: 1 ( ) b T w - w T Hw E w E 0 Proven fact: = + + - - 2 ] T d t g w t [ ( ) η d t ( ) ( ) , η ≥ + 1 + + 1 = 0 0 • Assume: implies W • mutually conjugate vectors . d i ) T Hd t ( ( ) d t (H-orthogonality) + 1 = 0 • Initial weight vector w 1 . Key: need to construct consecutive search directions d that are conjugate ( H -orthogonal)! w ∗ W (Side note: What is the implicit assumption of SD?) Question: How to converge to in (at most) steps?
Step-wise optimization Linear independence of conjugate directions W w ∗ ∑ ( ) α i d i (why can I do this?) Theorem : For a positive-definite square matrix H H , - – = w 1 { d 1 d 2 … d k , , , } orthogonal vectors are linearly i = 1 independent . W Proof : Linear independence: ∑ w ∗ α i d i = w 1 + α 1 d 1 α 2 d 2 … α k d k α i ∀ i i + + + = 0 iff. = 0 , . = 1 j – 1 ∑ ≡ α i d i w j w 1 + i = 1 α j d j w j = w j + + 1 Linear independence of conjugate Linear independence of conjugate directions directions α 1 d i T Hd 1 α 2 d i T Hd 2 … α k d i T Hd k Linear independence: + + + = 0 α 1 d 1 α 2 d 2 … α k d k α i ∀ i + + + = iff. = 0 , . 0 reduces to: T H α i d i T Hd i Pre-multiply by d i : = 0 T Hd 1 T Hd 2 T Hd k T H0 α 1 d i α 2 d i … α k d i + + + = d i However: T Hd i > (by assumption) T Hd 1 T Hd 2 T Hd k d i 0 α 1 d i α 2 d i … α k d i + + + = 0 Therefore: α i ∈ { 1 2 … k , , , } i ❏ T Hd j = 0 , ∀ ≠ i j Note (by assumption): d i = 0 , .
Linear independence of conjugate Step-wise optimization directions W w ∗ ∑ ( ) α i d i (Ah-ha!) From linear independence: – = w 1 i = 1 • H -orthogonal vectors d i form a complete basis set. • Any vector v can be expressed as: W ∑ w ∗ α i d i = w 1 + W ∑ α i d i i v = = 1 i = 1 j – 1 ∑ ≡ α i d i w j w 1 + i = 1 So, why did we need this result? α j d j w j = w j + + 1 α j So where are we now? Computing the correct step size W Given: a set of conjugate vectors d i . On locally quadratic surface, can converge to minimum in, W W at most, steps using: w ∗ ∑ ( ) α i d i – = w 1 α j d j { 1 2 … W , , , } j i w j = w j + , = . = 1 + 1 T H Pre-multiply by d j : W Big Questions: ∑ T H w ∗ T H ( ) α i d i d j – w 1 = d j α j • How to choose step size ? i = 1 W • How to construct conjugate directions d j ? ∑ T H w ∗ ( ) α i d j T Hd i d j – w 1 = • How can we do everything without computing ? H i = 1
α j α j Computing the correct step size Computing the correct step size Also: W 1 T H w ∗ ∑ T Hd i ( ) α i d j ( ) b T w - w T Hw E w E 0 – = d j w 1 = + + - - 2 i = 1 ( ) = + g w b Hw By H -orthogonality (conjugacy assumed): At minimum: T H w ∗ T Hd j ( ) α j d j d j – w 1 = (why?) g w ∗ ( ) = 0 Hw ∗ b + = 0 Hw ∗ = – b α j α j Computing the correct step size Computing the correct step size j T H w ∗ T b T Hd j ( ) – 1 ( ) α j d j – + d j Hw 1 d j – w 1 = ∑ α j α i d i = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - w j = w 1 + T Hd j d j i = 1 Hw ∗ = – b T H Pre-multiply by d j : So: j – 1 ∑ T Hw j T Hw 1 T Hd i α i d j T T Hd j = + . ( ) α j d j d j d j – – = d j b Hw 1 i = 1 T b T Hd j ( ) α j d j T Hw j T Hw 1 – d j + Hw 1 = d j = d j . T b T b ( ) ( ) – + – + d j Hw 1 d j Hw j α j α j (what’s the problem?) = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - T Hd j T Hd j d j d j
α j Computing the correct step size Important consequence W Theorem : Assuming a -dimensional quadratic error T b ( ) – + d j Hw j α j surface, = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - T Hd j d j 1 ( ) b T w - w T Hw E w E 0 = + + - - 2 = + g j b Hw j i ∈ { 1 2 … W , , , } and H -orthogonal vectors d i , : So: α j d j = + w j w j T g j + 1 – d j α j (woo-hoo!) = - - - - - - - - - - - - - - - - T Hd j T g j d j – d j α j = - - - - - - - - - - - - - - - - T Hd j d j w ∗ W will converge in at most steps to the minimum (for what error surface?). Why is this so? Orthogonality of gradient to previous search directions g j = b + Hw j FACT: T g j ∀ < , k j d k = 0 α j d j w j = w j + + 1 So: How is this important? ( ) g j – g j = H w j – w j How is this different from steepest descent? + 1 + 1 ( ) α j d j w j – w j = + 1 α j Hd j g j – g j = Let’s show that this is true... + 1
Recommend
More recommend