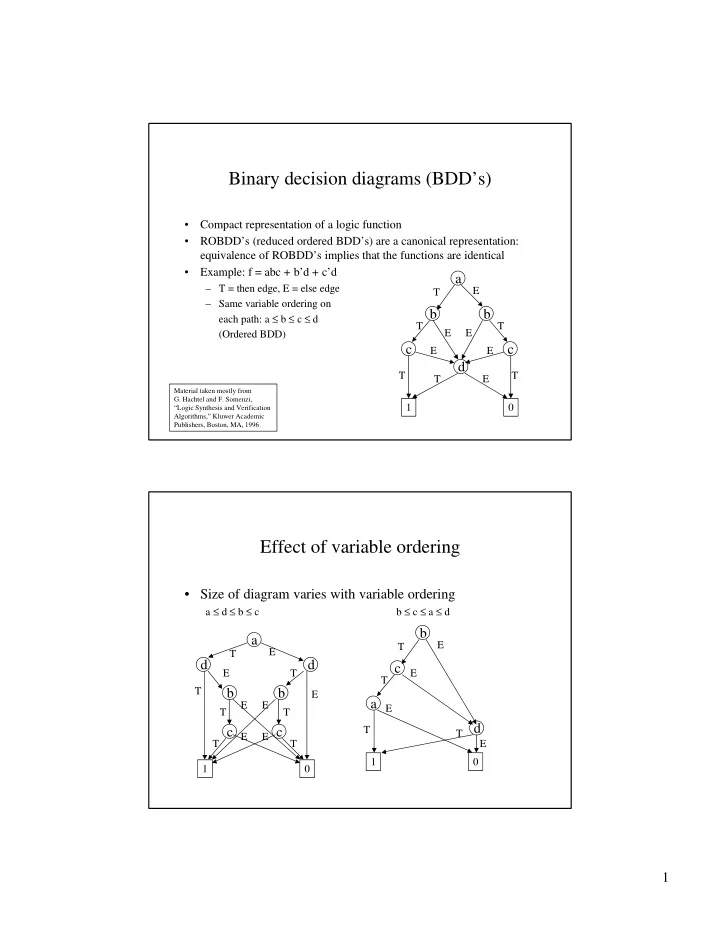
Binary decision diagrams (BDDs) Compact representation of a logic - PDF document

Binary decision diagrams (BDD’s) • Compact representation of a logic function • ROBDD’s (reduced ordered BDD’s) are a canonical representation: equivalence of ROBDD’s implies that the functions are identical • Example: f = abc + b’d + c’d a – T = then edge, E = else edge E T – Same variable ordering on b b each path: a ≤ b ≤ c ≤ d T T E E (Ordered BDD) c c E E d T T T E Material taken mostly from G. Hachtel and F. Somenzi, 1 0 “Logic Synthesis and Verification Algorithms,” Kluwer Academic Publishers, Boston, MA, 1996. Effect of variable ordering • Size of diagram varies with variable ordering a ≤ d ≤ b ≤ c b ≤ c ≤ a ≤ d b a E T E T d d c E T E T T b b E a E E E T T d T c c T E E T T E 1 0 1 0 1

Relation to the Shannon expansion • Each node is basically a Shannon expansion – f = a f a + a’ f a’ f a f a E f a’ T b b T T E E c c E E d T T T E 1 0 Building a BDD from a Shannon expansion f = abc + b’d + c’d b T E f b = ac + c’d c f bc’ = d T E f b’ = d f bc = a (… and so on …) 2

BDD as a compact truth table • Truth table: complete ordered binary tree • Reduce this by combining isomorphic parts and removing redundant nodes (T,E point to same node) to get ROBDD redundant b T E b c c T E T E T E c c TT d E d T E T E a E T T redundant E T d d d d 1 0 T E T E T E T E 1 1 1 0 0 0 a a T E T E BDD shown earlier for the ordering isomorphic b ≤ c ≤ a ≤ d 1 0 1 0 isomorphic Multioutput BDD’s • (Notation: solid line = Then edge; dashed line = Else edge) • Example: F 1 = b+c, F 2 = a+ b+c Combined Multioutput BDD Separate BDD’s F 2 F 2 F 1 F 1 a a b b b c c c 1 0 1 0 1 0 3

Compactness of BDD’s • BDD’s are successful at compactly representing many common functions – XOR is an example of a function with a large SOP/POS representation, but a very compact BDD • Worst case: O(2 n ) nodes – Functions that require this many nodes do exist • Can use multilevel techniques to represent BDD’s more compactly (“partitioned ROBDD’s”) Operations on BDD’s • Given BDD’s for functions f and g, can use Shannon expansion to see how operations are performed – Assume variables v 1 , v 2 … v n – f <op> g = v 1 (f <op> g) v1 + v 1 ’ (f <op> g) v1’ = v 1 (f v1 <op> g v1 ) + v 1 ’ (f v1’ <op> g v1’ ) – Can now do this recursively – Pictorially: v 1 T E (BDD for f v1 <op> g v1 ) (BDD for f v1’ <op> g v1’ ) – Identify identical subtrees as we come up the recursion tree using a hashing function 4