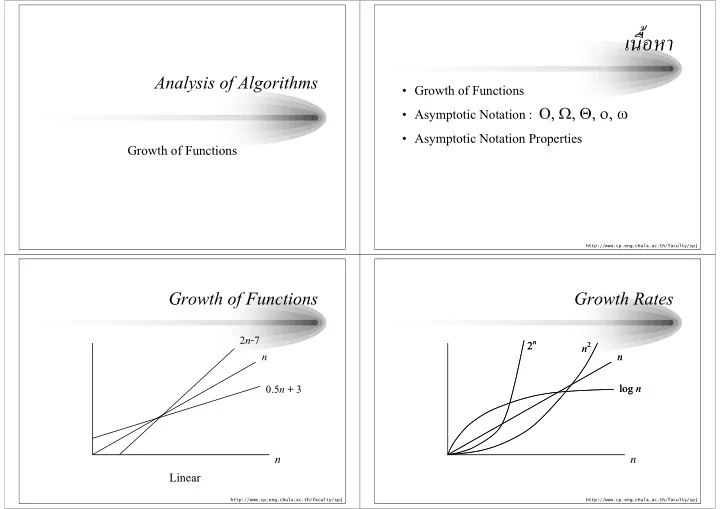
Analysis of Algorithms Growth of Functions Asymptotic Notation : - PowerPoint PPT Presentation

������ Analysis of Algorithms � Growth of Functions � Asymptotic Notation : Ο, Ω, Θ, ο, ω � Asymptotic Notation Properties Growth of Functions http://www.cp.eng.chula.ac.th/faculty/spj Growth of Functions Growth Rates 2 n -7 2 n 2 n n 2 n 2 n n n log n log n 0.5 n + 3 n n Linear http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

f ( n ) � g ( n ) Growth Rates � lim f ( n ) / g ( n ) = 0 0 f ( n ) grows slower than g ( n ) n → ∞ f ( n ) � g ( n ) : f ( n ) grows slower than g ( n ) ∞ f ( n ) grows faster than g ( n ) lim f ( n ) / g ( n ) = 0.5 n � 1 � log n � log 6 n � n 0.5 � n 3 � 2 n � n ! n → ∞ otherwise f ( n ) and g ( n ) have the same growth rate http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj l'H ô pital's Rule lg n vs. n f ( n ) lg n g ( n ) n = = Every sublinear function If f ( n ) and g ( n ) are differentiable, lim f ( n ) = ∞ lg ln , n n lim lim = n → ∞ n → ∞ n → ∞ grows faster than any ln 2 n n 1 ln n lim g ( n ) = ∞ , and lim f ' ( n ) / g ' ( n ) exists, then lim polylogarithmic function = n → n → ∞ ∞ ln 2 n → ∞ n e.g., n 0.01 vs. ( log n ) 100 1 1 n lim = lim f ( n ) / g ( n ) = lim f ' ( n ) / g ' ( n ) ( ) ln 2 n → ∞ 1 2 n n → n → ∞ ∞ d ln n 1 2 = l / n lim d n = ln 2 n → ∞ n d n = 1 / (2 n ) 0 = d n http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

Asymptotic Asymptotic Notations � Deal with the behaviour of functions in the limit y = 1 + x 2 (for sufficiently large value of its parameters) � Permit substantial simplification asymptotes (napkin mathematic, rough order of magnitude) � Classify functions by their growth rates Asymptotic : any approximation value that gets closer and closer to the truth, when some parameter approaches a limiting value. http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj �Same� Growth Rates �No Faster Than� Growth Rates 1 1 ... ... 12 n 0.5 + log n 12 n 0.5 + log n 2 n 5 + n 3 2 n 5 + n 3 100 100 ... ... ... ... ... 2 log n ... 2 log n 2 n 0.5 + 10 7 2 n 0.5 + 10 7 9 n 5 + 2 9 n 5 + 2 3 100 ... 3 100 ... 50 log n + 9 50 log n + 9 ... ... 6 n log n + n 6 n log n + n ... ... 7 log n ! 7 log n ! Θ (log n ) Θ ( n 0.5 ) Θ ( n 5 ) Ο (log n ) Ο ( n 0.5 ) Ο ( n 5 ) Θ (1) Θ ( n log n ) Ο (1) Ο ( n log n ) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

�Slower Than� Growth Rates �No Slower Than� Growth Rates 1 1 ... ... 12 n 0.5 + log n 12 n 0.5 + log n 2 n 5 + n 3 2 n 5 + n 3 100 100 ... ... ... ... ... 2 log n ... 2 log n 2 n 0.5 + 10 7 2 n 0.5 + 10 7 9 n 5 + 2 9 n 5 + 2 3 100 ... 3 100 ... 50 log n + 9 50 log n + 9 ... ... 6 n log n + n 6 n log n + n ... ... 7 log n ! 7 log n ! ο (2 n ) ο (log n ) ο ( n 0.5 ) ο ( n 3 ) Ω ( n 0.5 ) Ω ( n 5 ) ο ( n ) Ω (1) Ω (log n ) Ω ( n log n ) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj �Faster Than� Growth Rates Special Orders of Growth 1 : Θ ( 1 ) ... � constant 12 n 0.5 + log n 2 n 5 + n 3 : Θ ( log n ) 100 � logarithmic ... ... ... 2 log n � polylogarithmic : Θ ( log c n ) , c ≥ 1 2 n 0.5 + 10 7 9 n 5 + 2 3 100 ... : Θ ( n a ) , 0 < a < 1 � sublinear 50 log n + 9 ... : Θ ( n ) 6 n log n + n � linear ... : Θ ( n 2 ) � quadratic 7 log n ! : Θ ( n c ) , c ≥ 1 � polynomial ω ( n 0.1 ) ω ( n 4 ) : Θ ( c n ) , c > 1 ω (1) ω ( n ) � exponential http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

Analogy O-notation � f ( n ) and g ( n ) f and g (real numbers) O( g ( n )) = { f ( n ) :there exist positive constants � f ( n ) = Θ ( g ( n )) ≈ f = g c and n 0 such that � f ( n ) = Ο ( g ( n )) ≈ f ≤ g 0 ≤ f ( n ) ≤ c g ( n ) for all n ≥ n 0 } � f ( n ) = ο ( g ( n )) ≈ f < g � f ( n ) = Ω ( g ( n )) ≈ f ≥ g 27 n 2 + 0.5 n ∈ O( n 3 ) ? � f ( n ) = ω ( g ( n )) ≈ f > g 27 n 2 + 0.5 n ≤ n 3 for all n ≥ ??? ? 10 3 100 0 999 0 Not all functions are asymptotically comparable n vs. n 1 + sin n http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj Ω -notation Asymptotic Upper Bound c g ( n ) Ω ( g ( n )) = { f ( n ) :there exist positive constants c and n 0 such that f ( n ) 0 ≤ c g ( n ) ≤ f ( n ) for all n ≥ n 0 } 27 n 2 + 0.5 n ∈ Ω ( n ) ? n ≤ 27 n 2 + 0.5 n for all n ≥ 1 0 26 0 100 4 ??? ? n n 0 f ( n ) = O( g ( n ) ) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

Θ -notation Asymptotic Lower Bound Θ ( g ( n )) = { f ( n ) :there exist positive constants f ( n ) c 1 , c 2 , and n 0 such that 0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) for all n ≥ n 0 } c g ( n ) 27 n 2 + 0.5 n ∈ Θ ( n 2 ) ? n 2 ≤ 27 n 2 + 0.5 n ≤ n 2 for all n ≥ 27 28 0 ??? ??? ? 1 999 0 n n 0 f ( n ) = Ω ( g ( n ) ) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj ο -notation and ω -notation Asymptotic Tight Bound c 2 g ( n ) f ( n ) f ( n ) = ο ( g ( n ) ) f ( n ) = ω ( g ( n ) ) f ( n ) f ( n ) c 1 g ( n ) lim = ∞ lim = 0 lim lim g ( n ) g ( n ) n → n → ∞ ∞ n → n → ∞ ∞ n n 0 f ( n ) = Θ ( g ( n ) ) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

Asymptotic Notation Properties Transitivity � f ( n ) = Θ ( g ( n )) and g ( n ) = Θ ( h ( n )) imply f ( n ) = Θ ( h ( n )) � Transitivity � f ( n ) = Ο ( g ( n )) and g ( n ) = Ο ( h ( n )) imply f ( n ) = Ο ( h ( n )) � Reflexivity � f ( n ) = Ω ( g ( n )) and g ( n ) = Ω ( h ( n )) imply f ( n ) = Ω ( h ( n )) � Symmetry � f ( n ) = ο ( g ( n )) and g ( n ) = ο ( h ( n )) imply f ( n ) = ο ( h ( n )) � Transpose symmetry � f ( n ) = ω ( g ( n )) and g ( n ) = ω ( h ( n )) imply f ( n ) = ω ( h ( n )) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj Reflexivity Symmetry and Transpose Symmetry � f ( n ) = Θ ( f ( n ) ) � f ( n ) = Θ ( g ( n ) ) if and only if g ( n ) = Θ ( f ( n ) ) � f ( n ) = Ο ( f ( n ) ) � f ( n ) = Ο ( g ( n ) ) if and only if g ( n ) = Ω ( f ( n ) ) � f ( n ) = Ω ( f ( n ) ) � f ( n ) = ο ( g ( n ) ) if and only if g ( n ) = ω ( f ( n ) ) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj

Example Θ, Ω, Ο n k k + 1 ( ) � f ( n ) = Θ ( g ( n ) ) if and only if ∑ i = Θ n i 1 = � f ( n ) = Ω ( g ( n ) ) and n n n n k k k k ∑ i ≤ ∑ n ∑ i ≥ ∑ i i 1 i 1 i 1 i  n / 2  = = = = � f ( n ) = Ο ( g ( n ) ) k n k 1   + n n = ≥ ∑   Ο Ω  2    i n / 2 = k 1 + ( ) = Ο n k   n n ≥   2  2  k + 1 n k + 1 ( ) = Ω = n k 1 2 + http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj Example Logarithms log n ! = Θ ( n log n ) � Asymptotically, in logarithm, n ! = n × ( n -1) × ... × 2 × 1 � the base of the log does not matter ≤ n × n × ... × n × n = n n Ο log n ! ≤ log n n � log b n = ( log c n ) / ( log c b ) = O( n log n ) � log 10 n = ( log 2 n ) / ( log 2 10 ) = Θ ( log n ) n ! = n × ( n -1) × ... × ( n / 2) × ( n / 2-1) × ... × 2 × 1 � any polynomial function of n does not matter Ω ≥ n / 2 × n / 2 × ... × n / 2 × 1 × ... × 1 × 1 � log n 30 = 30 log n = Θ ( log n ) ≥ ( n / 2) n / 2 log n ! ≥ ( n / 2) log ( n / 2) � lg, ln, log = Ω ( n log n ) (CS) (math) (asymptotic) http://www.cp.eng.chula.ac.th/faculty/spj http://www.cp.eng.chula.ac.th/faculty/spj