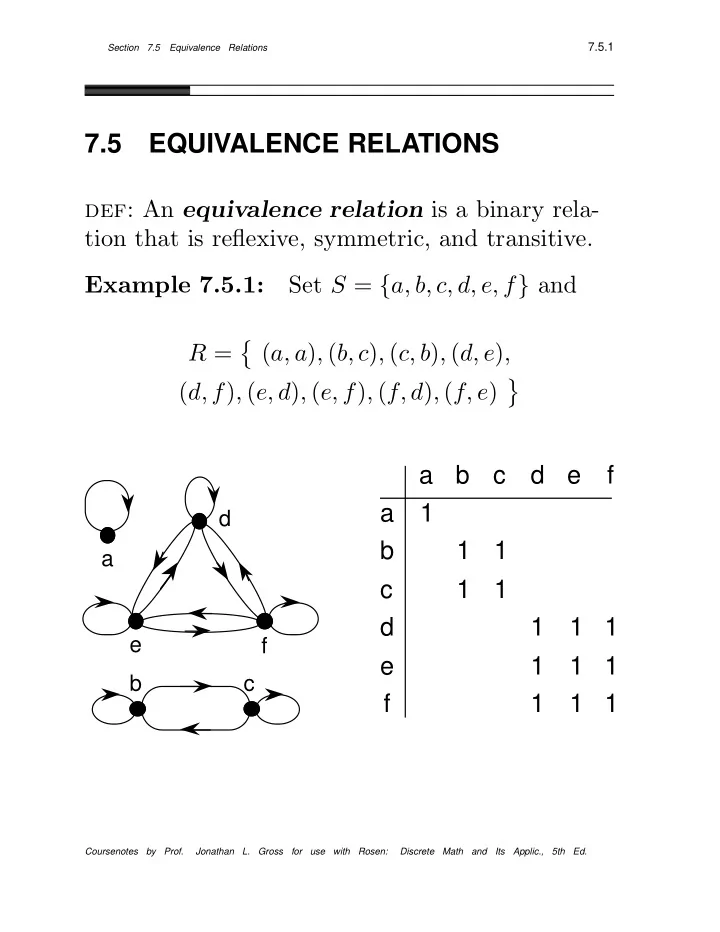
7.5 EQUIVALENCE RELATIONS def: An equivalence relation is a binary - PDF document

Apr 11, 2023 •254 likes •312 views

7.5.1 Section 7.5 Equivalence Relations 7.5 EQUIVALENCE RELATIONS def: An equivalence relation is a binary rela- tion that is reflexive, symmetric, and transitive. Set S = { a, b, c, d, e, f } and Example 7.5.1: R = ( a, a ) , ( b, c )

7.5.1 Section 7.5 Equivalence Relations 7.5 EQUIVALENCE RELATIONS def: An equivalence relation is a binary rela- tion that is reflexive, symmetric, and transitive. Set S = { a, b, c, d, e, f } and Example 7.5.1: � R = ( a, a ) , ( b, c ) , ( c, b ) , ( d, e ) , � ( d, f ) , ( e, d ) , ( e, f ) , ( f, d ) , ( f, e ) a b c d e f a 1 d b 1 1 a c 1 1 d 1 1 1 e f e 1 1 1 b c f 1 1 1 Coursenotes by Prof. Jonathan L. Gross for use with Rosen: Discrete Math and Its Applic., 5th Ed.
7.5.2 Chapter 7 RELATIONS Prop 7.5.1. Let R be an equivalence relation. Then every component of the digraph of R is a ♦ complete digraph. Cor 7.5.2. An equivalence relation induces a partition on its domain. The vertex set of each component of Proof: the digraph is a cell of the partition. ♦ Prop 7.5.3. Let R be an equivalence relation. Order its domain so that the elements of each cell of the induced partition occur contiguously. The resulting matrix represention has blocks of square matrices of all 1’s down its main diagonal and has all zeroes for its other entries. ♦ Coursenotes by Prof. Jonathan L. Gross for use with Rosen: Discrete Math and Its Applic., 5th Ed.
7.5.3 Section 7.5 Equivalence Relations FINITE EQUIVALENCE RELATIONS 2 × 2 checkerboards Example 7.5.2: There are 16 checkerboards. Checkerboard x is related to checkerboard y if it can be trans- formed into y by a rotation or by a reflection. relation R = sibling of Example 7.5.3: domain = all persons The reflexive, trans. closure of R is an eq rel. It partitions all of humanity into equivalence classes of (full) siblings. Coursenotes by Prof. Jonathan L. Gross for use with Rosen: Discrete Math and Its Applic., 5th Ed.
7.5.4 Chapter 7 RELATIONS INFINITE EQUIVALENCE RELATIONS domain = rational fractions Example 7.5.4: � p � � � p, q ∈ Z , q � = 0 � q a b and c Then are related if ad = bc d The partition cells are rational fractions of equal value. COUNTING PROBLEM (solved in w4205): How many cells are there if p, q ∈ { 1 , . . . , 10 } ? domain Z Example 7.5.5: eq. rel. = congruence mod 3 Equivalence Classes: [0] 3 = { . . . , − 6 , − 3 , 0 , 3 , 6 , 9 , . . . } [1] 3 = { . . . , − 5 , − 2 , 1 , 4 , 7 , 10 , . . . } [2] 3 = { . . . , − 4 , − 1 , 2 , 5 , 8 , 11 , . . . } domain = propositions on Example 7.5.6: p, q (infinite domain – arbitrarily long strings) eq. rel. = logical equivalence N.B. there are 2 4 cells to this partition Coursenotes by Prof. Jonathan L. Gross for use with Rosen: Discrete Math and Its Applic., 5th Ed.

Recommend

Equivalence Relations {( a , b ) | a and b are from the the same state}. Observe that these

Equivalence Relations http://localhost/~senning/courses/ma229/slides/equivalence-relations/slide01.html Equivalence Relations http://localhost/~senning/courses/ma229/slides/equivalence-relations/slide02.html Equivalence Relations prev | slides

235 views • 4 slides

Todays Expedition TED highlights Equivalence Relations Equivalence Classes and

Todays Expedition TED highlights Equivalence Relations Equivalence Classes and Partitions Boolean Algebra Boolean functions Sum of Products expansion Logic gates and circuits Sections 8.5, 11.1-11.3 in the text

541 views • 15 slides

Section 4.2: Equivalence Relations What is equality? What is equivalence? Equality is

Section 4.2: Equivalence Relations What is equality? What is equivalence? Equality is more basic, fundamental concept. Every element in a set is equal only to itself. The basic equality relation {(x,x) | x S} We tend to assume

893 views • 61 slides

THE KNUTH RELATIONS HUAN VO Abstract. We define three equivalence relations on the set of words

THE KNUTH RELATIONS HUAN VO Abstract. We define three equivalence relations on the set of words using different means. It turns out that they are the same relation. 1. Motivation Recall the algorithm of row inserting an entry x into a tableau T .

239 views • 10 slides

Affine Toric Equivalence Relations are Effective Claudiu Raicu University of California, Berkeley

Affine Toric Equivalence Relations are Effective Claudiu Raicu University of California, Berkeley AMS-SMM Joint Meeting, Berkeley, June 2010 Motivating Question Under what circumstances do quotients by finite equivalence relations exist?

879 views • 39 slides

A decision procedure for equivalence relations Sbastien Michelland with Pierre Corbineau,

Congruence closure Equivalence and inclusions Quantified hypotheses Conclusion A decision procedure for equivalence relations Sbastien Michelland with Pierre Corbineau, Lionel Rieg and Karine Altisen July 5, 2020 1 / 14 (CC BY-ND)

660 views • 22 slides

Polishable Borel equivalence relations S lawomir Solecki Cornell University Research

Polishable Borel equivalence relations S lawomir Solecki Cornell University Research supported by NSF grant DMS1700426 June 2018 Outline Outline of Topics Introduction 1 Polishable equivalence relations 2 Canonical approximations

415 views • 28 slides

Equivalence uandvarestrongly Relations connected. u G * * v AND v G * * u AND

MathematicsforComputerScience two-waywalks MIT 6.042J/18.062J walkfromutovand backfromvtou: Equivalence uandvarestrongly Relations connected. u G * * v AND v G * * u AND AlbertRMeyer

81 views • 5 slides

Forcing, Equivalence Relations and Marker Structures S. Jackson (joint with S. Gao, E. Krohne,

Forcing, Equivalence Relations and Marker Structures S. Jackson (joint with S. Gao, E. Krohne, and B. Seward) Department of Mathematics University of North Texas August, 2013 Chapman University S. Jackson Forcing, Equivalence Relations and

589 views • 32 slides

Equality and equivalence relations in formal proofs Pierre CORBINEAU DCS day, Autrans, 26-27

A short introduction to myself Equality and equivalence relations in Coq Equality and equivalence relations in formal proofs Pierre CORBINEAU DCS day, Autrans, 26-27 march 2009 A short introduction to myself Equality and equivalence relations

647 views • 25 slides

CSCI 246 Class 16 MORE EQUIVALENCE RELATIONS Quiz Questions Lecture 27: What is the

CSCI 246 Class 16 MORE EQUIVALENCE RELATIONS Quiz Questions Lecture 27: What is the difference between an equivalence relation and a partial order relation? Notes and Clarifications Extra credit due tonight Quiz option for

295 views • 25 slides

Equivalence Relations and Subgroups Toby Kenney with R. Par and R. Wood Mathematics, Dalhousie

Equivalence Relations and Subgroups Toby Kenney with R. Par and R. Wood Mathematics, Dalhousie University, Halifax, Canada CT07 2007JN1723 Toby Kenney with R. Par and R. Wood Equivalence Relations and Subgroups Quantales Recall that

406 views • 21 slides

Countable Borel equivalence relations, recursion theory, and Borel combinatorics Andrew Marks UC

Countable Borel equivalence relations, recursion theory, and Borel combinatorics Andrew Marks UC Berkeley Countable Borel equivalence relations Definition A Borel equivalence relation E is an equivalence relation on 2 that has a 0

567 views • 56 slides

Borel equivalence relations and symmetric models Topologies for the Friedman-Stanley jumps Assaf

Borel equivalence relations and symmetric models Topologies for the Friedman-Stanley jumps Assaf Shani UCLA Logic colloquium, Udine, Italy July 2018 1 / 7 Motivation Given an equivalence relation E on a Polish space X , how does E behave

225 views • 7 slides

Thin Projective Equivalence Relations and Inner Models Philipp Schlicht University of Mnster,

Thin Projective Equivalence Relations and Inner Models Philipp Schlicht University of Mnster, Germany Logic Colloquium Wrocaw, 14-19 July 2007 Definition. An equivalence relation E is called thin if there is no perfect set

279 views • 13 slides

Borel equivalence relations and symmetric models Assaf Shani CMU, Harvard Special session on

Borel equivalence relations and symmetric models Assaf Shani CMU, Harvard Special session on choiceless set theory and related areas Denver, January 2020 1 / 8 Friedman-Stanley jumps Definition Let E be an equivalence relation on X . A

209 views • 8 slides

Lecture 4.2: Equivalence relations and equivalence classes Matthew Macauley Department of

Lecture 4.2: Equivalence relations and equivalence classes Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4190, Discrete Mathematical Structures M. Macauley (Clemson) Lecture

561 views • 11 slides

Cryptographic Logical Relations What is the contextual equivalence for cryptographic

Cryptographic Logical Relations What is the contextual equivalence for cryptographic protocols and how to prove it? Yu ZHANG Including joint work with J. Goubault-Larrecq, D. Nowak and S. Lasota EVEREST, INRIA Sophia-Antipolis February

487 views • 37 slides

Borel equivalence relations and the Laver forcing Michal Doucha Charles University in Prague and

Borel equivalence relations and the Laver forcing Michal Doucha Charles University in Prague and Institute of Mathematics, AS July 8th, 2012 Michal Doucha Borel equivalence relations and the Laver forcing Introduction Vladimir Kanovei, Marcin

952 views • 30 slides

Discrete Mathematics in Computer Science Equivalence Relations and Partitions Malte Helmert,

Discrete Mathematics in Computer Science Equivalence Relations and Partitions Malte Helmert, Gabriele R oger University of Basel Relations: Recap A relation over sets S 1 , . . . , S n is a set R S 1 S n . Possible

1.25k views • 88 slides

Above countable products of countable equivalence relations Assaf Shani UCLA European Set

Above countable products of countable equivalence relations Assaf Shani UCLA European Set Theory Conference, Vienna July 2019 The -jumps of Clemens and Coskey Definition (Clemens-Coskey) Let E be an equivalence relation on X and a

108 views • 9 slides

Borel equivalence relations and weak choice principles Assaf Shani UCLA ASL meeting, Macomb,

Borel equivalence relations and weak choice principles Assaf Shani UCLA ASL meeting, Macomb, Illinois May 2018 1 / 10 Motivation Suppose E is a Borel equivalence relation on X and c : X I is a ( natural ) complete classification.

721 views • 10 slides

A coinductive approach to -equivalence relations jww Simon Boulier and Nicolas Tabareau

A coinductive approach to -equivalence relations jww Simon Boulier and Nicolas Tabareau (INRIA Nantes) Egbert Rijke Carnegie Mellon University erijke@andrew.cmu.edu September 8th 2017, Oxford Overview & Goals To formulate in

816 views • 24 slides

Equivalence relations in mathematics, K-16+ Art Duval Department of Mathematical Sciences

Definitions and motivation Examples More theory Equivalence relations in mathematics, K-16+ Art Duval Department of Mathematical Sciences University of Texas at El Paso AMS Southeastern Sectional Meeting University of Louisville October 5,

1.07k views • 84 slides