1
play

1 Big-omega Big-theta v1.2 7 v1.2 8 Establishing rate of - PDF document

Feb 22, 2024 •206 likes •273 views

Types of formulas for basic operation count Exact formula e.g., C( n ) = n ( n -1)/2 Algorithms, Design and Analysis Formula indicating order of growth with specific multiplicative constant e.g., C( n ) 0.5 n 2 Big-Oh analysis,

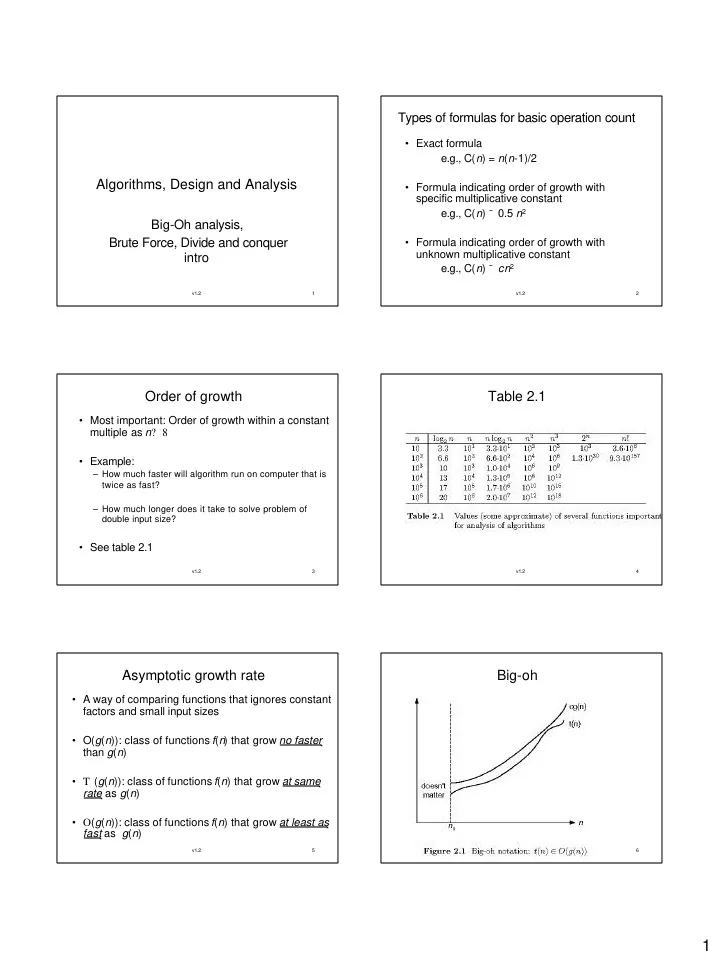
  1. Types of formulas for basic operation count • Exact formula e.g., C( n ) = n ( n -1)/2 Algorithms, Design and Analysis • Formula indicating order of growth with specific multiplicative constant e.g., C( n ) ˜ 0.5 n 2 Big-Oh analysis, Brute Force, Divide and conquer • Formula indicating order of growth with unknown multiplicative constant intro e.g., C( n ) ˜ cn 2 v1.2 1 v1.2 2 Order of growth Table 2.1 • Most important: Order of growth within a constant multiple as n ? 8 • Example: – How much faster will algorithm run on computer that is twice as fast? – How much longer does it take to solve problem of double input size? • See table 2.1 v1.2 3 v1.2 4 Asymptotic growth rate Big-oh • A way of comparing functions that ignores constant factors and small input sizes • O( g ( n )): class of functions f ( n ) that grow no faster than g ( n ) • T ( g ( n )): class of functions f ( n ) that grow at same rate as g ( n ) • O ( g ( n )): class of functions f ( n ) that grow at least as fast as g ( n ) v1.2 5 v1.2 6 1

  2. Big-omega Big-theta v1.2 7 v1.2 8 Establishing rate of growth: Method 1 – using L’Hôpital’s rule limits If 0 order of growth of T ( n) n) < order of growth of g ( n ) • lim n ? 8 f ( n ) = lim n ? 8 g ( n ) = 8 c >0 order of growth of T ( n) n) = order of growth of g ( n ) lim n ? 8 T ( n )/ g ( n ) = • and the derivatives f ´ , g ´ exist, order of growth of T ( n) n) > order of growth of g ( n ) 8 Then Examples: Examples: f ( n ) f f ´( ´( n ) lim lim lim lim vs. 2 n 2 • 10 n = g ( n ) g ´( g ´( n ) n ? 8 ? 8 n ? 8 ? 8 • n ( n +1)/2 vs. n 2 • Example: Example: log log n vs. vs. n • log b n vs. log c n v1.2 9 v1.2 10 Establishing rate of growth: Method 2 – using Basic Asymptotic Efficiency classes definition • f ( n ) is O( g ( n )) if order of growth of f ( n ) = 1 constant order of growth of g ( n ) (within constant log n logarithmic multiple) n linear • There exist positive constant c and non- negative integer n 0 such that n log n n log n n 2 quadratic f ( n ) = c g ( n ) for every n = n 0 n 3 cubic Examples: 2 n exponential • 10 n is O(2 n 2 ) n! factorial • 5 n +20 is O(10 n ) v1.2 11 v1.2 12 2

  3. Big-Oh Rules More Big-Oh Examples 7n-2 7n-2 is O(n) 0 ≥ 1 such that 7n-2 ≤ c• n for n ≥ n 0 • If is f ( n ) a polynomial of degree d , then f ( n ) is need c > 0 and n this is true for c = 7 and n 0 = 1 O ( n d ) , i.e., � 3n 3 + 20n 2 + 5 1. Drop lower-order terms 3n 3 + 20n 2 + 5 is O(n 3 ) 2. Drop constant factors 0 ≥ 1 such that 3n 3 + 20n 2 + 5 ≤ c• n 3 for n ≥ n 0 need c > 0 and n • Use the smallest possible class of functions this is true for c = 4 and n 0 = 21 – Say “ 2 n is O ( n ) ” instead of “ 2 n is O ( n 2 ) ” � 3 log n + log log n • Use the simplest expression of the class 3 log n + log log n is O(log n) – Say “ 3 n + 5 is O ( n ) ” instead of “ 3 n + 5 is O (3 n ) ” 0 ≥ 1 such that 3 log n + log log n ≤ c•log n for n ≥ n 0 need c > 0 and n this is true for c = 4 and n 0 = 2 v1.2 13 v1.2 14 Intuition for Asymptotic Brute Force Notation A straightforward approach usually based on problem statement and definitions Big-Oh Examples: – f(n) is O(g(n)) if f(n) is asymptotically less than or equal to g(n) 1. Computing a n ( a > 0, n a nonnegative big-Omega integer) – f(n) is Ω (g(n)) if f(n) is asymptotically greater than or equal to g(n) big-Theta – f(n) is Θ (g(n)) if f(n) is asymptotically equal to g(n) 2. Computing n ! little-oh – f(n) is o(g(n)) if f(n) is asymptotically strictly less than g(n) little-omega 3. Selection sort – f(n) is ω (g(n)) if is asymptotically strictly greater than g(n) 4. Sequential search v1.2 15 v1.2 16 More brute force algorithm examples: Brute force strengths and weaknesses • Closest pair • Strengths: – wide applicability – Problem: find closest among n points in k - – simplicity dimensional space – yields reasonable algorithms for some important problems – Algorithm: Compute distance between each pair of • searching points • string matching – Efficiency : • matrix multiplication – yields standard algorithms for simple computational tasks • sum/product of n numbers • Convex hull • finding max/min in a list – Problem: find smallest convex polygon enclosing n • Weaknesses: points on the plane – rarely yields efficient algorithms – Algorithm: For each pair of points p 1 and p 2 – some brute force algorithms unacceptably slow determine whether all other points lie to the same – not as constructive/creative as some other design side of the straight line through p 1 and p 2 techniques – Efficiency : v1.2 17 v1.2 18 3

  4. Divide and Conquer Divide-and-conquer technique The most well known algorithm design a problem of size n strategy: 1. Divide instance of problem into two or subproblem 1 subproblem 2 more smaller instances of size n /2 of size n /2 2. Solve smaller instances recursively a solution to a solution to subproblem 1 subproblem 2 3. Obtain solution to original (larger) instance by combining these solutions a solution to the original problem v1.2 19 v1.2 20 General Divide and Conquer recurrence: Divide and Conquer Examples where f ( n ) ? T ( n k ) T ( n ) = aT ( n/b ) + f ( n ) • Sorting: mergesort and quicksort 1. a < b k T ( n ) ? T ( n k ) • Tree traversals T ( n ) ? T ( n k lg n ) 2. a = b k • Binary search 3. a > b k T ( n ) ? T ( n log b a ) • Matrix multiplication-Strassen’s algorithm Note: the same results hold with O instead of T . • Convex hull-QuickHull algorithm v1.2 21 v1.2 22 Mergesort Mergesort Example Algorithm: 7 2 1 6 4 • Split array A[1.. n ] in two and make copies of each half in arrays B[1.. n /2 ] and C[1.. n /2 ] • Sort arrays B and C • Merge sorted arrays B and C into array A as follows: – Repeat the following until no elements remain in one of the arrays: • compare the first elements in the remaining unprocessed portions of the arrays • copy the smaller of the two into A, while incrementing the index indicating the unprocessed portion of that array – Once all elements in one of the arrays are processed, copy the remaining unprocessed elements from the other array into A. v1.2 23 v1.2 24 4

  5. Efficiency of mergesort Quicksort • All cases have same efficiency: T ( n log n ) • Select a pivot (partitioning element) • Rearrange the list so that all the elements in the positions before the pivot are smaller than or equal to • Number of comparisons is close to theoretical the pivot and those after the pivot are larger than the minimum for comparison-based sorting: pivot (See algorithm Partition in section 4.2) – log n ! ˜ n lg n - 1.44 n • Exchange the pivot with the last element in the first (i.e., = sublist) – the pivot is now in its final position • Space requirement: T ( n ) (NOT in-place) • Sort the two sublists p • Can be implemented without recursion (bottom-up) A[ i ]= p A[ i ]> p v1.2 25 v1.2 26 The partition algorithm Quicksort Example 15 22 13 27 12 10 20 25 v1.2 27 v1.2 28 Efficiency of quicksort QuickHull Algorithm • Best case : split in the middle — T ( n log n ) Inspired by Quicksort compute Convex Hull: Worst case : sorted array! — T ( n 2 ) • • Assume points are sorted by x -coordinate values • Average case : random arrays — T ( n log n ) • Identify extreme points P 1 and P 2 (part of hull) • Compute upper hull: • Improvements: – find point P max that is farthest away from line P 1 P 2 – better pivot selection: median of three partitioning avoids – compute the hull of the points to the left of line P 1 P max worst case in sorted files – compute the hull of the points to the left of line P max P 2 – switch to insertion sort on small subfiles – elimination of recursion • Compute lower hull in a similar manner P max these combine to 20-25% improvement P 2 • Considered the method of choice for internal sorting for large files ( n = 10000) P 1 v1.2 29 v1.2 30 5

  6. Efficiency of QuickHull algorithm • Finding point farthest away from line P 1 P 2 can be done in linear time • This gives same efficiency as quicksort: – Worst case : T ( n 2 ) – Average case : T ( n log n ) • If points are not initially sorted by x-coordinate value, this can be accomplished in T ( n log n ) — no increase in asymptotic efficiency class • Other algorithms for convex hull: – Graham’s scan – DCHull also in T ( n log n ) v1.2 31 6

Recommend

More recommend