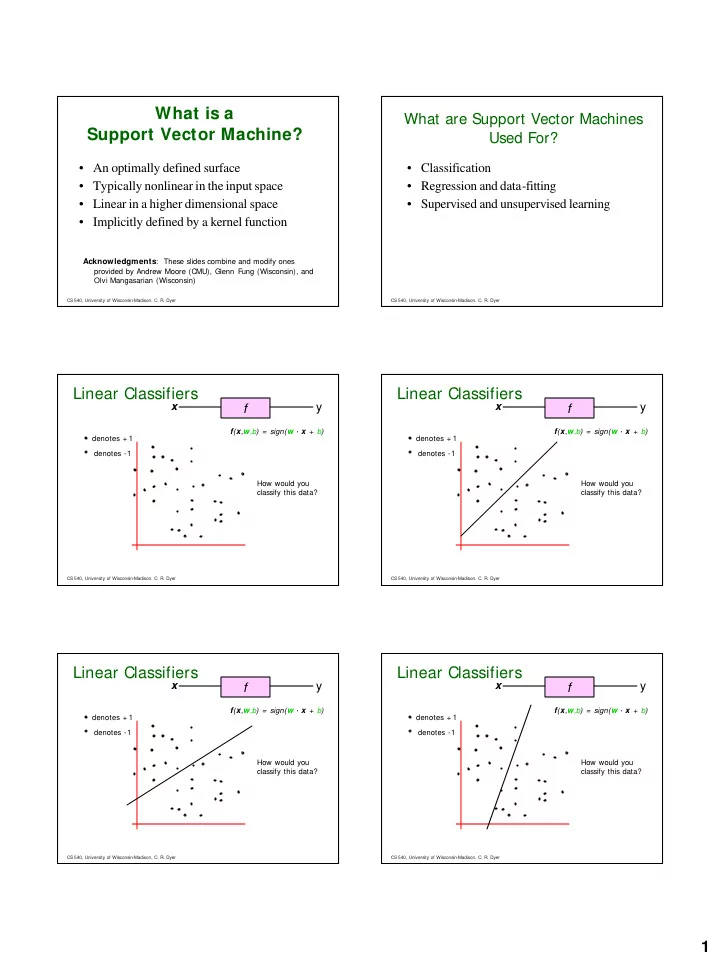
what is a
play

What is a What are Support Vector Machines Support Vector Machine? - PDF document

Jan 13, 2023 •479 likes •577 views

What is a What are Support Vector Machines Support Vector Machine? Used For? An optimally defined surface Classification Typically nonlinear in the input space Regression and data-fitting Linear in a higher dimensional

  1. What is a What are Support Vector Machines Support Vector Machine? Used For? • An optimally defined surface • Classification • Typically nonlinear in the input space • Regression and data-fitting • Linear in a higher dimensional space • Supervised and unsupervised learning • Implicitly defined by a kernel function Acknowledgments : These slides combine and modify ones provided by Andrew Moore (CMU), Glenn Fung (Wisconsin), and Olvi Mangasarian (Wisconsin) CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Linear Classifiers Linear Classifiers x y x y f f f ( x , w ,b) = sign( w · x + b) f ( x , w ,b) = sign( w · x + b) denotes + 1 denotes + 1 denotes -1 denotes -1 How would you How would you classify this data? classify this data? CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Linear Classifiers Linear Classifiers x y x y f f f ( x , w ,b) = sign( w · x + b) f ( x , w ,b) = sign( w · x + b) denotes + 1 denotes + 1 denotes -1 denotes -1 How would you How would you classify this data? classify this data? CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer 1

  2. Linear Classifiers Classifier Margin x y x y f f f ( x , w ,b) = sign( w · x + b) f ( x , w ,b) = sign( w · x + b) denotes + 1 denotes + 1 Define the margin denotes -1 denotes -1 of a linear classifier as the Any of these width that the would be fine … boundary could be increased by before hitting a … but which is best? data point CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Maximum Margin Maximum Margin x y x y f f f ( x , w ,b) = sign( w · x + b) f ( x , w ,b) = sign( w · x + b) denotes + 1 denotes + 1 The maximum The maximum denotes -1 denotes -1 margin linear margin linear classifier is the classifier is the linear classifier linear classifier Support Vectors with the, um, with the, um, are those data maximum margin. maximum margin. points that the margin pushes This is the This is the up against simplest kind of simplest kind of # SV's < < # DP SVM (Called an SVM (Called an LSVM) LSVM) Linear SVM Linear SVM CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Why Maximum Margin? Specifying a Line and Margin lass = +1” Plus-Plane Classifier Boundary “Predict C 1. Intuitively this feels safest zone Minus-Plane f ( x , w ,b) = sign( w. x - b) 2. If we’ve made a small error in the -1” denotes + 1 “Predict Class = location of the boundary (it’s been The maximum jolted in its perpendicular direction) zone denotes -1 this gives us least chance of causing a margin linear misclassification classifier is the 3. Robust to outliers since the model is linear classifier Support Vectors immune to change/removal of any with the, um, are those data non-support-vector data points maximum margin. points that the 4. There’s some theory that is related to margin pushes • How do we represent this mathematically? This is the (but not the same as) the proposition up against simplest kind of that this is a good thing • … in m input dimensions? # SV's < < # DP SVM (Called an 5. Empirically it works very well LSVM) CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer 2

  3. Specifying a Line and Margin Computing the Margin lass = +1” lass = +1” Plus-Plane M = Margin (width) Classifier Boundary “Predict C “Predict C zone zone Minus-Plane -1” -1” How do we compute w “Predict Class = “Predict Class = M in terms of w wx+ b= 1 zone wx+ b= 1 zone wx+ b= 0 wx+ b= 0 and b ? wx+b= -1 wx+b= -1 • Plus-plane = { w · x + b = + 1 } • Plus-plane = { w x + b = + 1 } • Minus-plane = { w · x + b = -1 } • Minus-plane = { w x + b = -1 } • The vector w is perpendicular to the Plus Plane w · x + b ≥ 1 Classify as.. + 1 if i.e. sign() -1 if w · x + b = - 1 Universe if - 1 < w · x + b < 1 explodes CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Computing the Margin Computing the Margin lass = +1” lass = +1” x + M = Margin x + M = Margin “Predict C “Predict C zone zone -1” -1” How do we compute How do we compute w w x - x - “Predict Class = “Predict Class = M in terms of w M in terms of w wx+ b= 1 zone wx+ b= 1 zone wx+ b= 0 wx+ b= 0 and b ? and b ? wx+b= -1 wx+b= -1 • Plus-plane = { w x + b = + 1 } • Plus-plane = { w x + b = + 1 } • Minus-plane = { w x + b = -1 } • Minus-plane = { w x + b = -1 } The vector w is perpendicular to the Plus Plane The vector w is perpendicular to the Plus Plane • • Any location in Any location in Let x - be any point on the minus plane Let x - be any point on the minus plane • R m : not � m : not • necessarily a necessarily a Let x + be the closest plus-plane-point to x - Let x + be the closest plus-plane-point to x - • • datapoint data point Claim : x + = x - + λ w for some value of λ . Why? • CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Computing the Margin Computing the Margin lass = +1” lass = +1” M = Margin M = Margin x + x + “Predict C “Predict C zone zone The line from x - to x + is -1” -1” perpendicular to the How do we compute w w x - x - “Predict Class = “Predict Class = planes M in terms of w wx+ b= 1 zone wx+ b= 1 zone wx+ b= 0 So to get from x - to x + wx+ b= 0 and b ? wx+b= -1 wx+b= -1 travel some distance in What we know: Plus-plane = { w x + b = + 1 } direction w • w x + + b = + 1 • • Minus-plane = { w x + b = -1 } w x - + b = - 1 • The vector w is perpendicular to the Plus Plane • x + = x - + λ w • Let x - be any point on the minus plane • | x + - x - | = M Let x + be the closest plus-plane-point to x - • • Claim : x + = x - + λ w for some value of λ . Why? It’s now easy to get M • in terms of w and b CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer 3

  4. Computing the Margin Computing the Margin lass = +1” lass = +1” 2 x + M = Margin x + M = Margin = “Predict C “Predict C zone zone w . w -1” -1” w w x - x - “Predict Class = “Predict Class = wx+ b= 1 zone 2 wx+ b= 1 zone = w ( x - + λ w) + b = 1 ? M = | x + - x - | = | λ w | = wx+ b= 0 wx+ b= 0 w.w wx+b= -1 wx+b= -1 ⇒ = = | | . What we know: What we know: ? w ? w w w x - + b + λ ww = 1 w x + + b = + 1 w x + + b = + 1 • • w x - + b = -1 ⇒ w x - + b = - 1 • • 2 . 2 w w = = x + = x - + λ w x + = x - + λ w • • - 1 + λ ww = 1 . . w w w w | x + - x - | = M | x + - x - | = M • • ⇒ It’s now easy to get M It’s now easy to get M 2 = ? in terms of w and b in terms of w and b w.w CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Learning via Quadratic Programming Learning the Maximum Margin Classifier 2 lass = +1” x + M = Margin = w . w “Predict C zone • QP is a well-studied class of optimization -1” algorithms to maximize a quadratic function of w x - “Predict Class = some real-valued variables subject to linear wx+ b= 1 zone wx+ b= 0 constraints wx+b= -1 Given a guess of w and b we can • Compute whether all data points in the correct half -planes • Compute the width of the margin So now we just need to write a program to search the space of w ’s and b ’s to find the widest margin that matches all the data points. How ? CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer Uh-oh! This is going to be a problem! Uh-oh! This is going to be a problem! What should we do? What should we do? Idea: denotes + 1 denotes + 1 denotes -1 denotes -1 Minimize || w || 2 + C (distance of error points to their correct place) CS 540, University of Wisconsin-Madison, C. R. Dyer CS 540, University of Wisconsin-Madison, C. R. Dyer 4

Recommend

More recommend