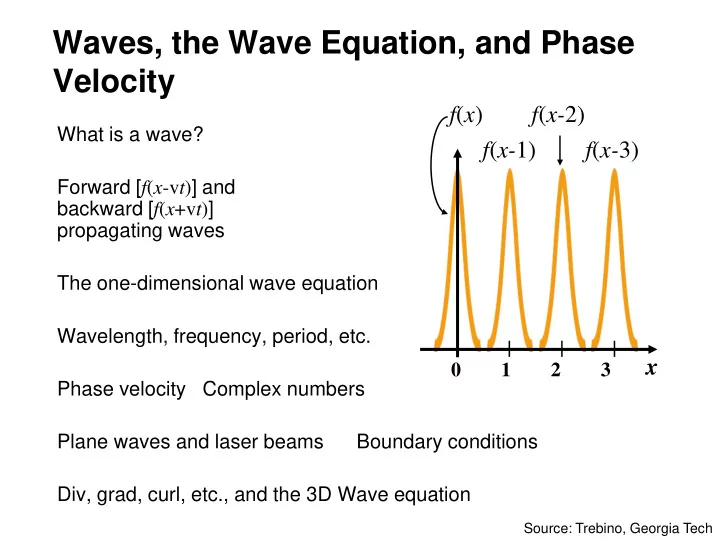
Waves, the Wave Equation, and Phase Velocity f ( x ) f ( x- 2) What - PowerPoint PPT Presentation

Waves, the Wave Equation, and Phase Velocity f ( x ) f ( x- 2) What is a wave? f ( x- 1) f ( x- 3) Forward [ f ( x -v t ) ] and backward [ f ( x +v t ) ] propagating waves The one-dimensional wave equation Wavelength, frequency, period, etc. x 0 1 2 3 Phase velocity Complex numbers Plane waves and laser beams Boundary conditions Div, grad, curl, etc., and the 3D Wave equation Source: Trebino, Georgia Tech

What is a wave? A wave is anything that moves. To displace any function f ( x ) to the right, just change its argument from x to x-a , where a is a positive number. f ( x ) f ( x- 2) If we let a = v t , where v is positive f ( x- 1) f ( x- 3) and t is time, then the displacement will increase with time. So represents a rightward, f ( x - v t ) or forward, propagating wave. Similarly, represents a f ( x + v t ) leftward, or backward, propagating wave. x 0 1 2 3 v will be the velocity of the wave.

The one-dimensional wave equation The one-dimensional wave equation for scalar (i.e., non-vector) functions, f : ∂ ∂ 2 2 1 f f − = 0 ∂ ∂ 2 2 2 v x t where v will be the velocity of the wave. The wave equation has the simple solution: = ± ( , ) ( v ) f x t f x t where f ( u ) can be any twice-differentiable function.

Proof that f ( x ± v t ) solves the wave equation ∂ ∂ u u = ± Write f ( x ± v t ) as f ( u ) , where u = x ± v t . So and = v 1 ∂ ∂ x t ∂ ∂ ∂ ∂ ∂ ∂ f f u f f u = = Now, use the chain rule: ∂ ∂ ∂ ∂ ∂ ∂ x u x t u t ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ 2 2 2 2 f f f f f f f f = = ± = = 2 So ⇒ and ⇒ v v ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ 2 2 2 2 x u t u t u x u Substituting into the wave equation:   ∂ ∂ ∂ ∂ 2 2 2 2 1 1 f f f f − = − = 2   v 0 ∂ ∂ ∂ ∂ 2 2 2 2 2 2 v v   x t u u

The 1D wave equation for light waves ∂ ∂ 2 2 E E where E is the − µε = 0 light electric field ∂ ∂ 2 2 x t We’ll use cosine- and sine-wave solutions: = ± + ± ( , ) cos[ ( v )] sin[ ( v )] E x t B k x t C k x t ± ( v) kx k t or = ± ω + ± ω ( , ) cos( ) sin( ) E x t B kx t C kx t ω where: 1 The speed of light in = = v vacuum, usually called µε k “c”, is 3 x 10 10 cm/s.

A simpler equation for a harmonic wave: E ( x,t ) = A cos[( kx – ω t ) – θ ] Use the trigonometric identity: cos( z – y ) = cos( z ) cos( y ) + sin( z ) sin( y ) where z = kx – ω t and y = θ to obtain: E ( x,t ) = A cos( kx – ω t ) cos( θ ) + A sin( kx – ω t ) sin( θ ) which is the same result as before, For simplicity, we’ll = − ω + − ω ( , ) cos( ) sin( ) E x t B kx t C kx t just use the forward- propagating wave. as long as: A cos( θ ) = B and A sin( θ ) = C

Definitions: Amplitude and Absolute phase E ( x,t ) = A cos[( k x – ω t ) – θ ] A = Amplitude θ = Absolute phase (or initial phase) π kx

Definitions Spatial quantities: Temporal quantities:

The Phase Velocity How fast is the wave traveling? Velocity is a reference distance divided by a reference time. The phase velocity is the wavelength / period: v = λ / τ Since ν = 1/ τ : v = λ v In terms of the k-vector, k = 2 π / λ , and v = ω / k the angular frequency, ω = 2 π / τ , this is:

The Phase of a Wave The phase is everything inside the cosine. E(x,t ) = A cos( ϕ ) , where ϕ = k x – ω t – θ ϕ = ϕ ( x,y,z,t ) and is not a constant, like θ ! In terms of the phase, ω = – ∂ ϕ / ∂ t k = ∂ ϕ / ∂ x And – ∂ ϕ / ∂ t This formula is useful v = ––––––– when the wave is ∂ ϕ / ∂ x really complicated.

Tacoma Narrows Bridge Animation: http://www.youtube.com/watch?v=3mclp9QmCGs 1. The animation shows the Tacoma Narrows Bridge shortly before its collapse. What is its frequency? A .1 Hz B .25 Hz C .50 Hz D 1 Hz 2. The distance between the bridge towers (nodes) was about 860 meters and there was also a midway node. What was the wavelength of the standing torsional wave? A 1720 m B 860 m C 430 m D There is no way to tell. 3. What is the amplitude? A 0.4 m B 4 m C 8 m D 16 m

Complex numbers Consider a point, P = ( x,y ) , on a 2D Cartesian grid. Let the x-coordinate be the real part and the y-coordinate the imaginary part of a complex number. So, instead of using an ordered pair, ( x , y ), we write: P = x + i y = A cos( ϕ ) + i A sin( ϕ ) where i = (-1) 1/2

Euler's Formula exp( i ϕ ) = cos( ϕ ) + i sin( ϕ ) so the point, P = A cos( ϕ ) + i A sin( ϕ ) , can be written: P = A exp( i ϕ ) where A = Amplitude ϕ = Phase

exp( i ϕ ) = cos( ϕ ) + i sin( ϕ ) Proof of Euler's Formula 2 3 x x x = + + + + ( ) (0) '(0) ''(0) '''(0) ... f x f f f f Use Taylor Series: 1! 2! 3! 2 3 4 x x x x = + + + + + exp( ) 1 ... x 1! 2! 3! 4! 2 4 6 8 x x x x = − + − + + cos( ) 1 ... x 2! 4! 6! 8! 3 5 7 9 x x x x x = − + − + + sin( ) ... x 1! 3! 5! 7! 9! ϕ ϕ ϕ ϕ 2 3 4 If we substitute x = i ϕ i i ϕ = + − − + + exp( ) 1 ... i into exp( x ) , then: 1! 2! 3! 4!     ϕ ϕ ϕ ϕ 2 4 3 = − + + + − + 1 ... ...     i  2! 4!   1! 3!  = ϕ + ϕ cos( ) sin( ) i

Complex number theorems ϕ = ϕ + ϕ exp( ) cos( ) sin( ) If i i π = − exp( ) 1 i π = exp( / 2) i i ϕ = ϕ − ϕ exp(- ) cos( ) sin( ) i i 1 [ ] ϕ = ϕ + − ϕ cos( ) exp( ) exp( ) i i 2 1 [ ] ϕ = ϕ − − ϕ sin( ) exp( ) exp( ) i i 2 i [ ] ϕ × ϕ = ϕ + ϕ exp( ) exp( ) exp ( ) A i A i A A i 1 1 2 2 1 2 1 2 [ ] ϕ ϕ = ϕ − ϕ exp( ) / exp( ) / exp ( ) A i A i A A i 1 1 2 2 1 2 1 2

More complex number theorems Any complex number, z , can be written: z = Re{ z } + i Im{ z } So Re{ z } = 1/2 ( z + z* ) and Im{ z } = 1/2 i ( z – z* ) where z * is the complex conjugate of z ( i → – i ) The "magnitude," | z | , of a complex number is: | z | 2 = z z* = Re{ z } 2 + Im{ z } 2 To convert z into polar form, A exp( i ϕ ) : A 2 = Re{ z } 2 + Im{ z } 2 tan( ϕ ) = Im{ z } / Re{ z }

We can also differentiate exp( ikx ) as if the argument were real. d = exp( ) exp( ) ikx ik ikx dx Proof : d [ ] + = − + cos( ) sin( ) sin( ) cos( ) kx i kx k kx ik kx dx   1 = − + sin( ) cos( ) ik kx kx     i [ ] − = = + But 1/ , so: sin( ) cos( ) i i ik i kx kx

Waves using complex numbers The electric field of a light wave can be written: E ( x,t ) = A cos( kx – ω t – θ ) Since exp( i ϕ ) = cos( ϕ ) + i sin( ϕ ) , E ( x,t ) can also be written: We often E ( x,t ) = Re { A exp[ i ( kx – ω t – θ )] } write these expressions or without the E ( x,t ) = 1/2 A exp[ i ( kx – ω t – θ )] + c.c. ½, Re, or +c.c. where " + c.c. " means "plus the complex conjugate of everything before the plus sign."

Waves using complex amplitudes We can let the amplitude be complex: ( ) ( ) =  − ω − θ  , exp E x t A i kx t   { } ( ) { } ( ) = − θ  − ω  , ex p ( ) ex p E x t A i i k x t   where we've separated the constant stuff from the rapidly changing stuff. The resulting "complex amplitude" is: = − i θ ← exp( ) (note the " ~ ") E A 0  ( ) ( ) So: As written, this entire = − ω , exp E x t E i kx t 0 field is complex!   How do you know if E 0 is real or complex? Sometimes people use the "~", but not always. So always assume it's complex.

Complex numbers simplify waves! Adding waves of the same frequency, but different initial phase, yields a wave of the same frequency. This isn't so obvious using trigonometric functions, but it's easy with complex exponentials: = − ω + − ω + − ω ( , ) exp ( ) exp ( ) exp ( ) E x t E i kx t E i kx t E i kx t 1 2 3  tot    = + + − ω ( )exp ( ) E E E i kx t 1 2 3    where all initial phases are lumped into E 1 , E 2 , and E 3 .

− ω is called a plane wave. 0 exp[ ( )] E i kx t  A plane wave’s contours of maximum field, called wave-fronts or phase-fronts , are planes. They extend over all space. A wave's wave- Wave-fronts fronts sweep are helpful along at the for drawing speed of light. pictures of interfering waves. A plane wave's wave-fronts are equally spaced, a wavelength apart. Usually, we just draw lines; it’s They're perpendicular to the propagation easier. direction.

Localized waves in space: beams A plane wave has flat wave-fronts throughout all space. It also has infinite energy. It doesn’t exist in reality. Real waves are more localized. We can approximate a realistic wave as a plane wave vs. z times a Gaussian in x and y :   + 2 2 x y = − − ω ( , , , ) exp exp[ ( ) ]   E x y z t E i kz t 0   2   w z exp( -x 2 ) w y Laser beam x Localized wave-fronts x spot on wall