The Evolution of Geometric Structures on 3-Manifolds Curtis T - PowerPoint PPT Presentation

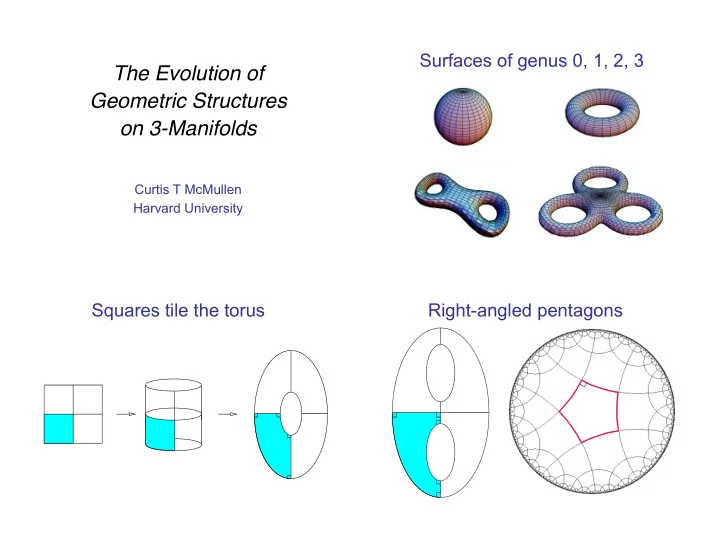
Surfaces of genus 0, 1, 2, 3 The Evolution of Geometric Structures on 3-Manifolds Curtis T McMullen Harvard University Squares tile the torus Right-angled pentagons

Uniformization All surfaces can be built using one of 3 geometries Hyperbolic surfaces = algebraic curves y 2 = x 5 -1 Klein Poincaré 1870s g=0 g=1 g=2,3,4, … 1881 G H To produce algebraic functions on /G: Poincaré series H � f = f ( z ) dz 2 g ∗ ( f ) Θ ( f ) = g ∈ G holomorphic quadratic differential on H The world of 3-manifolds The Geometrization Conjecture Thurston, 1982 All 3-manifolds can be built using just 8 geometries. Perelman, 2003

The 3-sphere The Eight Geometries constant curvature E 3 H 3 S 3 S 1 → M →∑ g S 1 xS 1 → M → S 1 torus g ≥ 2 sphe re elliptic parab hyperbolic R × S 2 E 3 R × H E 3 Nil R ⇥ R 2 ⇥ S 3 Nil SL 2 R Products and twisted products: dimension 2+1/2 Hyperbolic Geometry Poincaré’s fake sphere, M=S 3 /G

⇒ ⇒ Fermat’s Last Theorem Poincaré Conjecture Catalog of elliptic curves/Q The only solutions to The only solution to x n +y n = z n , π 1 (M 3 )=(1) is M 3 =S 3 . ( Cremona, n>2, are trivial. 1992 ) Modularity Conjecture Geometrization Conjecture Every elliptic curve E Every M 3 is built from over is dominated Q geometric pieces; typically by a modular curve, H 3 / Γ → M. H / Γ ( N ) → E. Arithmetic Examples Knot Theory SL 2 (Z[ ω ]) SL 2 (Z[i]) H 3 / Γ = S 3 \ K Mostow: Topology ⇒ Geometry

Hyperbolic volume as a topological invariant K = � π / 3 1 vol( S 3 − K ) = 6 ( π / 3) = 6 log 2 sin θ d θ 0 = 2.0298832128193... The Perko Pair Thurston’s breakthroughs 1980s Almost all knot complements are hyperbolic. Almost all surgeries of S 3 along knot and links yield hyperbolic manifolds. The result of gluing together two hyperbolic 3-manifolds is hyperbolic, unless it contains a Hoste, Thistlethwaite and Weeks, 1998 : 2-torus. The First 1,701,936 knots (Up to 16 crossings)

Evolution and gluing Evolution by curvature τ Hamilton, Perelman 3-manifold hyperbolic hyperbolic 3-manifold ← → Riemann surface boundary Theorem(Thurston) M/ τ hyperbolic ⇔ ⇔ π 1 (M/ τ ) does not contain Darwin recognized that his weak and negative force... could only Z 2 play [a] creative role if variation met three crucial requirements: σ ○ τ : Teich( ∂ M) → Teich( ∂ M) has a fixed point. copious in extent, small in range of departure from the mean, and isotropic. Teich( ∂ M), we have (Analytic approach: at a given X in Gould, 2002 |D σ | ≤ || Θ X ||; and || Θ X || < 1.) Evolution by curvature Singularities Perelman’s papers 2002-3 Singularities always undo connect sums Evolution with surgery continues for all time Eventually, architecture of M becomes visible Geometrization Conjecture is true Poincaré Conjecture is true Thanks to Dmitri Gekhtman

Iteration on Teich( ∂ M) Ricci flow Cosmological Corollary ``General relativity places no constraints on the topology of the Universe.’’ K>0 K=0 K<0 Iteration on Teich( ∂ M) Iteration on Teich( ∂ M) Ricci flow Ricci flow PL, geometric, C ∞ , infinite-dimensional, PL, geometric, C ∞ , infinite-dimensional, classical, algorithmic variable curvature classical, algorithmic variable curvature Bottom up Top down Uses hierarchy General

Iteration on Teich( ∂ M) Iteration on Teich( ∂ M) Ricci flow Ricci flow PL, geometric, C ∞ , infinite-dimensional, PL, geometric, C ∞ , infinite-dimensional, classical, algorithmic variable curvature classical, algorithmic variable curvature Bottom up Top down Bottom up Top down Uses hierarchy General Uses hierarchy General Holomorphic Holomorphic Monotone Monotone Contracting Contracting General case - Diffuse surgery, cone manifolds? Welcomes singularities Surfaces in 3-manifolds? The Jones polynomial (1983) Conjecture . If M is a closed hyperbolic 3-manifold, then a finite cover of M contains an incompressible surface. skein theory t -1 V + - tV - = (t 1/2 - t -1/2 ) V 0 V(O,t) = 1 Theorem (Kahn-Markovic). If M is a closed, hyperbolic 3-manifold, then π 1 (M) contains a surface group.

Jones polynomial for figure 8 knot Quantum fields (Witten) V(t) = t -2 -t -1 +1-t+t 2 ⟨ K ⟩ = ∫ Tr( ∮ A) e 2 π ik CS(A) DA K = (q 1/2 +q -1/2 ) V(K,1/q) q = exp(2 π i/(2+k)) → 1 as k → ∞ ⟨ unknot ⟩ → 2 Volume Conjecture Murakami-Murakami Kashaev n/ 2 � n − j ⇥ ⇤ ( − 1) j V ( K n − 2 j , t ) V n +1 ( K, t ) = j j =0 Cable K 2 for figure eight knot K 2 π log |V n (K,e 2 π i/n )| hyperbolic → vol(S 3 -K) n quantum fields general relativity