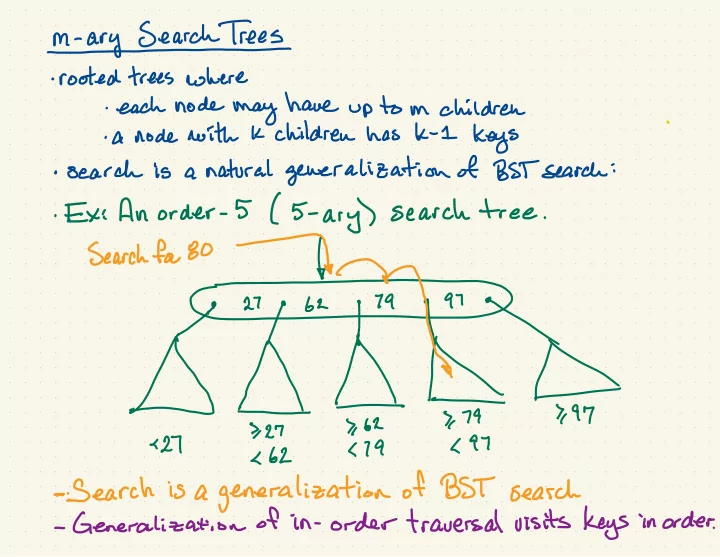

⇐ m-arysearchtree.sn rooted trees where • each node may have up to m children K children has k -1 keys . • a node with a natural generalization of BST search : • search is ' Exi An order - 5 ( 5- ar y ) search tree . search for 8\h is 779 262 727 L 97 < 27 179 , 62 - Search is a generalization of BST search - Generalization of in - order traversal visits keys in order .
Order m B- Tree ( As per textbook ) 5. search tree m - ar - data Items stored at leaves , keys in other nodes guide search - non - leaf nodes , other than the root have between TM1N and m children is a leaf M children , or • the root has between 2 and ith key non - heat is the smallest • in a node , the key stored in the ittst subtree same depth . all leaves are at the L keys ( for fixed L ) . leaves contain between Mil and some ( are fewer than Hd ( unless there . . ) . tree keys in the
B- Tree Search : Generalization of BST search . - Example , in an order -5 B- tree :( This tree : order 75 because of • must have * because of D.) be of order • must > 6 not Find 49 :\ ⑤ ¥ 0 " 3
sieetetteight.fi/Perfect''Trees-Aperfeetm-arytree- m - ary tree where : is an m children - every node has Zero or depth leaf has the same - every - A perfect m - ary tree of height h has the max # of a height - h m - ary tree nodes for . The number of nodes in a perfect m - airy tree of Fact : - height h is : mh M - I a perfect binary tree The number of nodes in for : - of height 2h11 h is .
The number of nodes at depth d. in a perfect ' of height at 2d binary tree least d is - Proof By induction on d 2d=2° = I Basis : D= 0 . an assume that I. It . Choose some d 70 is 2d nodes at depth d the number of Is . We must show that the number of nodes is 2d ? at depth dtt a perfect binary tree Since the tree is of height > dtl , every node at depth d 2 children . has nodes at depth dH , the number of So is 2. 2d = 2
in a perfect m - ary nodes at depth d The number of is md tree of height at least d . PI By induction on depth d- , and md=m° is just the root = I Basis : There D= 0 . assume the some d > 0 and Choose III. : md number of nodes at depth d is . : We must show that the number of nodes at II. is mdtt depth dtl . a perfect m - ary tree of Since the tree is height node at least dtt , every at depth d has m children . , the number of nodes at depth dtl So is = mdtl µ - Md M
⇒ Claim : Every - m B- tree of height h contains order least (E) h at keys . P¥ Observe that every m - ary B- tree of height - graph has a perfect (f) - cry tree as sub : h a ' n This subtree has (E) " leaves so the B- tree , does also . HE keys , Since each leaf least has at the B- tree contains at least CH2X math key 5.
1¥ : The height of B- tree with an order - m = 0 ( log n ) log m=n at most keys is n Let T be an order m B- tree with If : n nodes We have : ¥ )h - and height h . ± n n ) log ; n =0( log So h E ⇐ Searching for a key in a B- tree with can be done in time 0( log n ) n keys .
B-treeinserti.org/L=m-- 5) ① Insert 57 7 I *
⇒ After inserting 57 : . go [ This leaf will be " overfull " Now , insert 5 =D we spH ' ÷
After insertion of 554 splitting of leaf :
splittinganInternalhlodet-ns.at 407 ← . g④F%¥¥ * splitting the leaf ¥**¥t¥:¥I¥÷¥
Aftersplikinj 0
sphttingtheRoot.orerfullroyt.j.IT/.y?Newroot . 11111114k¥ TI THI bbb 'd Abb Ab 4 4 6 6 5 3 3 2 5 2 1 1 Tree just got taller same ( larger ) depth have the - Still , leaves all .
BTreeInsertij new key k belongs , call it Find the leaf where v. a insert K into v ) { while ( v over - full and not the root is split v. i v ← parent G) ¥ r is the over - full root and . split in two , v new root with two children i add a time • Claim : B - tree insertion can be done in n is the number of 0 ( log n ) , where keys in the tree .
I B-treeRemov L with the key K . Find the leaf to be removed - delete K from L K was the smallest key in L , correct the key in an ancestor - if - V ← L is not root ) { has too few keys - ( r and = while FY27 children )l if ( v has an adjacent sibling with more than - rom th I a key and child - or shift } else { of r v with a sibling merge v ← parent of the merged node g } is root and has only if I v one child , c ) new root . c is the delete vj
(0Iff=5 ) 5*1 ↳ IT ← 5k¥ THEE :* :* ¥ delete 52 delete 78 * ← µss¥*H 19 hI¥e# * tbh by ↳ It A ¥ : too small 4 too small keys Hr merge with sibling . a key ④ shift d- child and µ . . $1 1- Ff¥¥ Is → F¥F ⇒ %
↳ shiftingataninternaluodl.ua 'm III . too few & I ↳ ← A TIE . shift a keyt child . It ✓ e Hn * * i. ¥4 tool
whenamergeshrinksaninternalnode-T.IE ← ↳ Fol ← just too -1¥ got small because of a / IT 1 I 17 PM D D deletion $ merge Y 9- I l I 1 I /
whentherootgetstoosmall.LI ← ↳ Fol ← just -1¥ too got small / IT 1 . I 17 PM 17 17 $ merge to I I 1 I 1 /
Recommend
More recommend