Pr [ X i ] . i = 1 E [ X ] = Pr [ X i ] . i = 1 Proof: One has - PowerPoint PPT Presentation

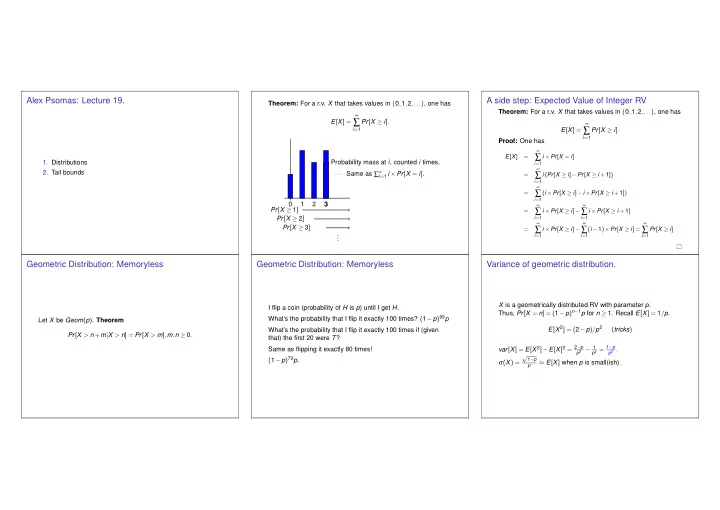
Alex Psomas: Lecture 19. A side step: Expected Value of Integer RV Theorem: For a r.v. X that takes values in { 0 , 1 , 2 ,... } , one has Theorem: For a r.v. X that takes values in { 0 , 1 , 2 ,... } , one has ∞ E [ X ] = ∑ Pr [ X ≥ i ] . ∞ ∑ i = 1 E [ X ] = Pr [ X ≥ i ] . i = 1 Proof: One has ∞ ∑ E [ X ] = i × Pr [ X = i ] 1. Distributions Probability mass at i , counted i times. i = 1 ∞ 2. Tail bounds Same as ∑ ∞ ··· i = 1 i × Pr [ X = i ] . ∑ = i ( Pr [ X ≥ i ] − Pr [ X ≥ i + 1 ]) i = 1 ∞ ∑ = ( i × Pr [ X ≥ i ] − i × Pr [ X ≥ i + 1 ]) i = 1 0 1 2 3 ∞ ∞ Pr [ X ≥ 1 ] ∑ ∑ = i × Pr [ X ≥ i ] − i × Pr [ X ≥ i + 1 ] Pr [ X ≥ 2 ] i = 1 i = 1 ∞ ∞ ∞ Pr [ X ≥ 3 ] ∑ ∑ ∑ = i × Pr [ X ≥ i ] − ( i − 1 ) × Pr [ X ≥ i ] = Pr [ X ≥ i ] . . . i = 1 i = 1 i = 1 . Geometric Distribution: Memoryless Geometric Distribution: Memoryless Variance of geometric distribution. X is a geometrically distributed RV with parameter p . I flip a coin (probability of H is p ) until I get H . Thus, Pr [ X = n ] = ( 1 − p ) n − 1 p for n ≥ 1. Recall E [ X ] = 1 / p . What’s the probability that I flip it exactly 100 times? ( 1 − p ) 99 p Let X be Geom ( p ) . Theorem E [ X 2 ] = ( 2 − p ) / p 2 ( tricks ) What’s the probability that I flip it exactly 100 times if (given Pr [ X > n + m | X > n ] = Pr [ X > m ] , m , n ≥ 0 . that) the first 20 were T ? var [ X ] = E [ X 2 ] − E [ X ] 2 = 2 − p p 2 − 1 p 2 = 1 − p Same as flipping it exactly 80 times! p 2 . √ ( 1 − p ) 79 p . 1 − p σ ( X ) = ≈ E [ X ] when p is small(ish). p

Poisson Poisson Poisson Distribution: Definition and Mean Experiment: flip a coin n times. The coin is such that Pr [ H ] = λ / n . Random Variable: X - number of heads. Thus, X = B ( n , λ / n ) . Poisson Distribution is distribution of X “for large n .” Experiment: flip a coin n times. The coin is such that Pr [ H ] = λ / n . Definition Poisson Distribution with parameter λ > 0 Random Variable: X - number of heads. Thus, X = B ( n , λ / n ) . X = P ( λ ) ⇔ Pr [ X = m ] = λ m Poisson Distribution is distribution of X “for large n .” m ! e − λ , m ≥ 0 . We expect X ≪ n . For m ≪ n one has Fact: E [ X ] = λ . Pr [ X = m ] = λ m m ! e − λ . Poisson and Queueing. When to use Poisson Simeon Poisson The Poisson distribution is named after: Poisson: Distribution of how many events in an interval? If an event can occur 0,1,2,... times in an interval, Average: λ . and the average number of events per interval is λ What is the maximum number of customers you might see? and events are independent and the probability of an event in an interval is proportional to the interval’s length, Idea: Cut into intervals so that “sum of Bernoulli (indicators)”. n = 10 sub-intervals. then it might be appropriate to use Poisson distribution. Binomial distribution, if only one event/interval! Maybe more... Pr [ k events in interval ] = λ k k ! e − λ and more. As n goes to infinity...analyze ... Examples: photons arriving at a telescope, telephone calls � n p i ( 1 − p ) n − i . � .... Pr [ X = i ] = arriving in a system, the number of mutations on a strand of i derive simple expression. DNA per unit length... “Life is good for only two things: doing mathematics and ...And we get the Poisson distribution! teaching it.”

n µ µ n n a Review: Distributions Inequalities: An Overview Andrey Markov ◮ Bern ( p ) : Pr [ X = 1 ] = p ; E [ X ] = p ; Var [ X ] = p ( 1 − p ) ; Chebyshev � n p m ( 1 − p ) n − m , m = 0 ,..., n ; Distribution Markov ◮ B ( n , p ) : Pr [ X = m ] = � m E [ X ] = np ; Var [ X ] = np ( 1 − p ) ; p n p n p n Andrey Markov is best known for his work on ◮ U [ 1 ,..., n ] : Pr [ X = m ] = 1 n , m = 1 ,..., n ; stochastic processes. A primary subject of his E [ X ] = n + 1 research later became known as Markov 2 ; chains and Markov processes. Var [ X ] = n 2 − 1 � � p n 12 ; Pafnuty Chebyshev was one of his teachers. ◮ Geom ( p ) : Pr [ X = n ] = ( 1 − p ) n − 1 p , n = 1 , 2 ,... ; E [ X ] = 1 P r [ X > a ] P r [ | X − µ | > � ] p ; Var [ X ] = 1 − p p 2 ; ◮ P ( λ ) : Pr [ X = n ] = λ n n ! e − λ , n ≥ 0; E [ X ] = λ ; Var [ X ] = λ . Markov’s inequality A picture Markov Inequality Note The inequality is named after Andrey Markov, although it appeared earlier in the work of Pafnuty Chebyshev. It should be (and is sometimes) called Chebyshev’s first inequality. Theorem Markov’s Inequality (the fancy version) Assume f : ℜ → [ 0 , ∞ ) is nondecreasing. Then, for a non-negative random variable X A more common version of Markov is for f ( x ) = x : Pr [ X ≥ a ] ≤ E [ f ( X )] , for all a such that f ( a ) > 0 . Theorem For a non-negative random variable X , and any a > 0, f ( a ) Pr [ X ≥ a ] ≤ E [ X ] Proof: . a Observe that 1 { X ≥ a } ≤ f ( X ) f ( a ) . Indeed, if X < a , the inequality reads 0 ≤ f ( X ) / f ( a ) , which holds since f ( · ) ≥ 0. Also, if X ≥ a , it reads 1 ≤ f ( X ) / f ( a ) , which holds since f ( · ) is nondecreasing. Expectation is monotone: if X ( ω ) ≤ Y ( ω ) for all ω , then E [ X ] ≤ E [ Y ] . Therefore, E [ 1 { X ≥ a } ] ≤ E [ f ( X )] . f ( a )

Markov Inequality Example: Geom(p) Markov’s inequality example Markov’s inequality example p and E [ X 2 ] = 2 − p Let X ∼ Geom ( p ) . Recall that E [ X ] = 1 p 2 . Pr [ X ≥ a ] ≤ E [ X ] Flip a coin n times. Probability of H is p . X counts the number . a Choosing f ( x ) = x , we of heads. get X follows the Binomial distribution with parameters n and p . What is a bound on the probability that a random X takes value Pr [ X ≥ a ] ≤ E [ X ] = 1 X ∼ B ( n , p ) . ≥ than twice its’ expectation? ap . a E [ X ] = np . Say n = 1000 and p = 0 . 5. E [ X ] = 500. 1 2 . It can’t be that more than half of the people are twice above Markov says that Pr [ X ≥ 600 ] ≤ 1000 ∗ 0 . 5 = 5 6 ≈ 0 . 83 Choosing f ( x ) = x 2 , the average! 600 we get Actual probability: < 0 . 000001 What is a bound on the probability that a random X takes value Pr [ X ≥ a ] ≤ E [ X 2 ] = 2 − p ≥ than k times its’ expectation? Notice: Same bound for 10 coins and Pr [ X ≥ 6 ] p 2 a 2 . a 2 1 k . Chebyshev’s Inequality Chebyshev and Poisson Chebyshev’s inequality example Let X = P ( λ ) . Then, E [ X ] = λ and var [ X ] = λ . Thus, Pr [ | X − λ | ≥ n ] ≤ var [ X ] = λ n 2 . This is Pafnuty’s inequality: Flip a coin n times. Probability of H is p . X counts the number n 2 of heads. Theorem: X follows the Binomial distribution with parameters n and p . Pr [ | X − E [ X ] | ≥ a ] ≤ var [ X ] X ∼ B ( n , p ) . , for all a > 0 . a 2 E [ X ] = np . Var [ X ] = np ( 1 − p ) . Say n = 1000 and p = 0 . 5. E [ X ] = 500. Var [ X ] = 250. Proof: Let Y = | X − E [ X ] | and f ( y ) = y 2 . Then, Markov says that Pr [ X ≥ 600 ] ≤ 500 600 = 5 6 ≈ 0 . 83 = E [ | X − E [ X ] | 2 ] Pr [ Y ≥ a ] ≤ E [ f ( Y )] = var [ X ] Chebyshev says that Pr [ X ≥ 600 ] = Pr [ X − 500 ≥ 100 ] ≤ . 250 f ( a ) a 2 a 2 Pr [ | X − 500 | ≥ 100 ] ≤ 10000 = 0 . 025 Actual probability: < 0 . 000001 This result confirms that the variance measures the “deviations Notice: If we had 100 coins, the bound for Pr [ X ≥ 60 ] would be from the mean.” different.