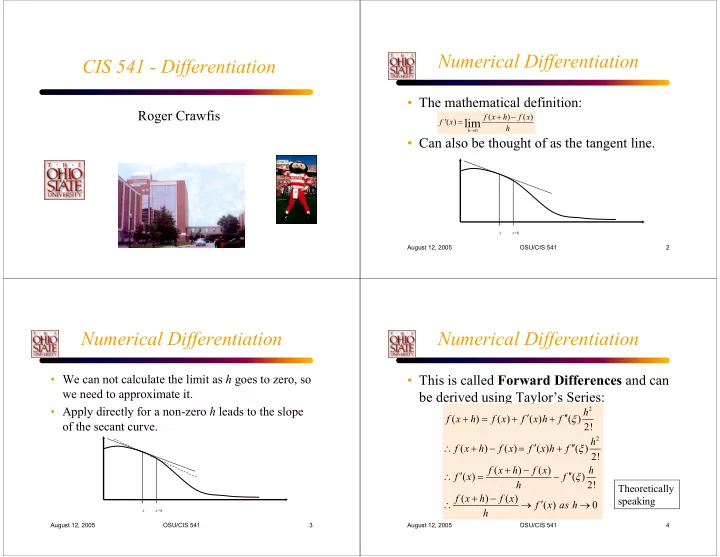
Numerical Differentiation CIS 541 - Differentiation The - PowerPoint PPT Presentation

Numerical Differentiation CIS 541 - Differentiation • The mathematical definition: Roger Crawfis + − f x ( h ) f x ( ) '( ) lim = f x h → h 0 • Can also be thought of as the tangent line. x x+h August 12, 2005 OSU/CIS 541 2 Numerical Differentiation Numerical Differentiation • We can not calculate the limit as h goes to zero, so • This is called Forward Differences and can we need to approximate it. be derived using Taylor’s Series: • Apply directly for a non-zero h leads to the slope 2 h + = + ′ + ′′ ξ f x ( h ) f x ( ) f ( ) x h f ( ) 2! of the secant curve. 2 h ′ ′′ ∴ + − = + ξ f x ( h ) f x ( ) f ( ) x h f ( ) 2! + − f x ( h ) f x ( ) h ′ ′′ ∴ = − ξ f ( ) x f ( ) 2! h Theoretically + − f x ( h ) f x ( ) speaking ′ ∴ → → f ( ) x as h 0 h x x+h August 12, 2005 OSU/CIS 541 3 August 12, 2005 OSU/CIS 541 4

Truncation Errors Error Tradeoff • Let f(x) = a+e, and f(x+h) = a+f. • Using a smaller step size reduces truncation error. • However, it increases the round-off error. • Then, as h approaches zero, e<<a and f<<a. • Trade off/diminishing returns occurs: Always think and test! • With limited precision on our computer, our Point of Total error diminishing representation of f(x) ≈ a ≈ f(x+h) . Log error returns • We can easily get a random round-off bit as Round off error the most significant digit in the subtraction. Truncation error • Dividing by h , leads to a very wrong answer for f’(x). Log step size August 12, 2005 OSU/CIS 541 5 August 12, 2005 OSU/CIS 541 6 Numerical Differentiation Numerical Differentiation • This formula favors (or biases towards) the • This leads to the Backward Differences right-hand side of the curve. formula. • Why not use the left? 2 h ′ ′′ − = − + ξ f x ( h ) f x ( ) f ( ) x h f ( ) 2! − − f x ( ) f x ( h ) h ′ ′′ ∴ = + ξ f ( ) x f ( ) 2! h − − f x ( ) f x ( h ) ′ ∴ → → f ( ) x as h 0 h x-h x x+h August 12, 2005 OSU/CIS 541 7 August 12, 2005 OSU/CIS 541 8

Numerical Differentiation Central Differences • Can we do better? • This formula does not seem very good. – It does not follow the calculus formula. • Let’s average the two: – It takes the slope of the secant with width 2h. + − − − + − − 1 ⎛ f x ( h ) f x ( ) f x ( ) f x ( h ) ⎞ f x ( h ) f x ( h ) ′ ≈ + = f ( ) x ⎜ ⎟ – The actual point we are interested in is not even ⎝ ⎠ 2 h h 2 h evaluated. Forward difference Backward difference • This is called the Central Difference formula. x-h x x+h August 12, 2005 OSU/CIS 541 9 August 12, 2005 OSU/CIS 541 10 Numerical Differentiation Central Differences • Is this any better? • The central differences formula has much • Let’s use Taylor’s Series to examine the error: better convergence. 2 3 h h + − − f x ( h ) f x ( h ) 1 + = + ′ + ′′ + ′′′ ξ [ ] f x ( h ) f x ( ) f ( ) x h f ( ) x f ( ) ′ ′′′ = − ζ 2 ζ ∈ − + f ( ) x f ( ) h , x h x , h 2 3! 2 h 6 2 3 h h ′ ′′ ′′′ − = − + − ς f x ( h ) f x ( ) f ( ) x h f ( ) x f ( ) • Approaches the derivative as h 2 goes to 2 3! subtracting zero!! + − − f x ( h ) f x ( h ) ( ) ′ ⎛ ⎞ = + h 3 h 3 2 f ( ) x O h ′ ′′′ ′′′ + − − = + ξ + ς f x ( h ) f x ( h ) 2 f ( ) x h f ( ) f ( ) ⎜ ⎟ 2 h 3! 3! ⎝ ⎠ August 12, 2005 OSU/CIS 541 11 August 12, 2005 OSU/CIS 541 12

Warning Richardson Extrapolation • Can we do better? • Still have truncation error problem. • Is my choice of h a good one? • Consider the case of: x = f x ( ) • Let’s subtract the two Taylor Series expansions again: 100 • Build a table with ⎢ x + h ⎥ ⎢ x − h ⎥ − ⎢ ⎥ ⎢ ⎥ ⎣ 100 ⎦ ⎣ 100 ⎦ h 2 h 3 h 4 h 5 ′ f ( ) x ฀ ( ) ( ) smaller values of h . + = + ′ + ′′ + ′′′ + 4 + 5 + f x ( h ) f x ( ) f ( ) x h f ( ) x f ( ) x f ( ) x f ( ) x L 2 h 2 3! 4! 5! at x = 1, h = 0.000333, with significant digits 6 2 3 4 5 • What about large h h h h − 0.0100033 0.0099966 ( ) ( ) ′ ′′ ′′′ − = − + − ς + 4 − 5 + ′ = f x ( h ) f x ( ) f ( ) x h f ( ) x f ( ) f ( ) x f ( ) x f ( ) x 0.010050 L ฀ 0.000666666 2 3! 4! 5! values of h for this Relative error: subtracting 0.01-0.010050 function? = ′′′ ′′′ 0.5% 5 f ( ) x f ( ) x h ( ) ′ 0.01 + − − = + 3 + 3 + 5 + f x ( h ) f x ( h ) 2 f ( ) x h 2 h 2 h 2 f ( ) x L 3! 3! 5! August 12, 2005 OSU/CIS 541 13 August 12, 2005 OSU/CIS 541 14 Richardson Extrapolation Richardson Extrapolation • Assuming the higher derivatives exist, we can • This function approximates f’(x) to O( h 2 ) as hold x fixed (which also fixes the values of f(x) ), we saw earlier. to obtain the following formula. • Let’s look at the operator as h goes to zero. 1 [ ] ′ = + − − + 2 + 4 + 6 + L f ( ) x f x ( h ) f x ( h ) a h a h a h 2 4 6 2 h ′ ϕ = − 2 − 4 − 6 − ( ) h f ( ) x a h a h a h L 2 4 6 2 4 6 h ⎛ h ⎞ ⎛ h ⎞ ⎛ h ⎞ • Richardson Extrapolation examines the operator ′ ϕ = − − − − ( ) f ( ) x a a a ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ L 2 4 6 2 ⎝ 2 ⎠ ⎝ 2 ⎠ ⎝ 2 ⎠ below as a function of h. 1 [ ] ϕ = + − − ( ) h f x ( h ) f x ( h ) Same leading constants 2 h August 12, 2005 OSU/CIS 541 15 August 12, 2005 OSU/CIS 541 16

Richardson Extrapolation Richardson Extrapolation • If h is small ( h <<1), then h 4 goes to zero • Using these two formula’s, we can come up with another estimate for the derivative that much faster than h 2 . cancels out the h 2 terms. • Cool!!! h 3 15 • Can we cancel out the h 6 term? ′ ϕ − ϕ = − − 4 − 6 − ( ) h 4 ( ) 3 f ( ) x a h a h L 4 6 2 4 16 – Yes, by using h/4 to estimate the derivative. or ⎡ ⎤ h 1 h ( ) Extrapolates by ′ = ϕ + ϕ − ϕ + f ( ) x ( ) ( ) ( ) h O h 4 ⎢ ⎥ assuming the new 2 3 ⎣ 2 ⎦ estimate undershot. new estimate difference between old and new estimates August 12, 2005 OSU/CIS 541 17 August 12, 2005 OSU/CIS 541 18 Richardson Extrapolation Richardson Extrapolation • Consider the following property : • Do not forget the formal definition is simply the central-differences formula: ∞ ∑ ϕ = ′ − ( ) h f ( ) x a h 2 k 2 k 1 [ ] = k 1 ϕ = + − − ( ) h f x ( h ) f x ( h ) ∞ 2 h ∑ = − 2 k L a h 2 k = k 1 • New symbology (is this a word?): • where L is unknown, ⎛ h ⎞ ( ) ′ ( ) = ϕ = L lim ( ) h f x ≡ ϕ D n ,0 ⎜ ⎟ n ⎝ 2 ⎠ h → 0 • as are the coefficients, a 2 k . 2 k ∞ ⎛ h ⎞ ∑ ( ) = + From previous slide L A k ,0 ⎜ ⎟ n ⎝ 2 ⎠ k = 1 August 12, 2005 OSU/CIS 541 19 August 12, 2005 OSU/CIS 541 20

Richardson Extrapolation Richardson Extrapolation • If we let h → h/ 2, then in general, we can • D(n,0) is just the central differences operator for different values of h. write: • Okay, so we proceed by computing D( n ,0) ⎛ ⎞ 4 1 ⎛ h ⎞ [ ] ′ = + − − + f ( ) x D n ( ,0) D n ( ,0) D n ( 1,0) O ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ − 4 1 ⎝ 2 n ⎠ for several values of n . ⎝ ⎠ • Recalling our cancellation of the h 2 term. • Let’s denote this operator as: ⎡ ⎤ h 1 h ( ) 1 ′ = ϕ + ϕ − ϕ + f ( ) x ( ) ( ) ( ) h O h 4 ( ) ( ) ( ) ⎢ ⎥ = + ⎡ − − ⎤ D n ,1 D n ( ,0) D n ,0 D n 1,0 ⎣ ⎦ 2 3 ⎣ 2 ⎦ 1 − 4 1 1 ( ) [ ] = + − + 4 D (1,0) D (1,0) D (0,0) O h − 4 1 August 12, 2005 OSU/CIS 541 21 August 12, 2005 OSU/CIS 541 22 Richardson Extrapolation Richardson Extrapolation • Now, we can formally define Richardson’s • Now, we can formally define Richardson’s extrapolation operator as: extrapolation operator as: m 1 4 1 ( ) ( ) ( ) ( ) ( ) ( ) = − − − − ≤ ≤ = − + ⎡ − − − − ⎤ D n m , D n m ( , 1) D n 1, m 1 , 1 m n D n m , D n m ( , 1) D n m , 1 D n 1, m 1 ⎣ ⎦ − − 4 m 1 4 m 1 − m 4 1 old estimate new estimate • or 1 Memorize me!!!! ( ) ( ) ( ) = − + ⎡ − − − − ⎤ D n m , D n m ( , 1) D n m , 1 D n 1, m 1 ⎣ ⎦ − 4 m 1 August 12, 2005 OSU/CIS 541 23 August 12, 2005 OSU/CIS 541 24