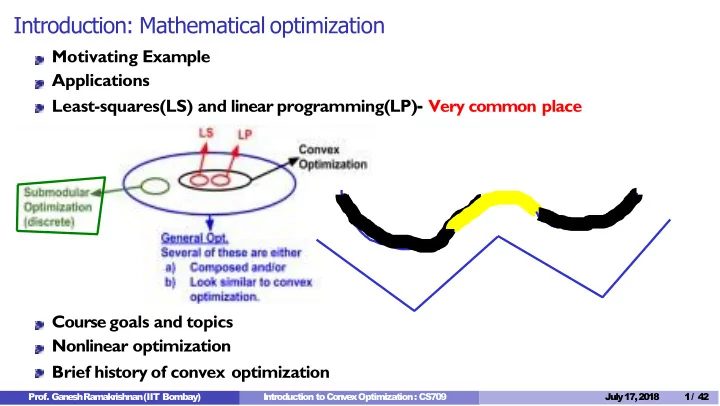
Introduction: Mathematical optimization Motivating Example - PowerPoint PPT Presentation

Introduction: Mathematical optimization Motivating Example Applications Least-squares(LS) and linear programming(LP) - Very common place Course goals and topics Nonlinear optimization Brief history of convex optimization Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 1/ 42

Almost Every Problem can be posed as an Optimization Problem G i v e n a s e t C ⊆ ℜ n find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat C⊆E . Hint: First work out the problem in lower dimensions x in C is a vector of size n C x = [x1,x2......xn] NEED A ROTATED+TRANSLATED VERSIO a2 Constraint: x1^2/a1^2 + x2^2/a2^2 a1 + ....xn^2/an^2 <= 1 Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 4 / 42

Almost Every Problem can be posed as an Optimization Problem G i v e n a s e t C⊆ ℜ n find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat C⊆E . Hint: First work out the problem in lower dimensions Sphere S r ⊆ ℜ c e n t e r e d at 0 is e x p r e s s e da s : n Sr = { ||x||_2 <= r} 2-norm is the square root of sum of squares of the individual components of x Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 4 / 42

Almost Every Problem can be posed as an Optimization Problem G i v e n a s e t C⊆ ℜ n find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat C⊆E . Hint: First work out the problem in lower dimensions Sphere S r ⊆ ℜ c e n t e r e d at 0 is e x p r e s s e d as: S r = { u ∈ ℜ n |∥ u ∥ 2 ≤ r } n Ellipsoid E⊆ ℜ n i s e x p r e s s e da s : Av + b A'u + b' Ellipsoid is a rotated, scaled and translated version of the sphere Our basic ellipsoid A' had A' = diagonal u mxn m n Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 4 / 42

Almost Every Problem can be posed as an Optimization Problem G i v e n a s e t C⊆ ℜ n find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat C⊆E . Hint: First work out the problem in lower dimensions Sphere S r ⊆ ℜ c e n t e r e d at 0 is e x p r e s s e d as: S r = { u ∈ ℜ n |∥ u ∥ 2 ≤ r } n Ellipsoid E⊆ ℜ n i s e x p r e s s e da s : { } { } E = v ∈ ℜ | A v + b ∈ S = v ∈ ℜ |∥ A v + b ∥ ≤ 1 . Here, A ∈S , that is, A is n n n 1 2 ++ an n × n (strictly) p o s it iv e definitematrix. The optimization p r o b l e m willbe: 3)That is, A has positive eigen values.. 1) A is an nxn matrix 4) The positive eigenvalues will (Sphere and Ellipsoid are both correspond to scaling of the axis in R^n) and corresponding eigenvectors 2) This brings an additional to the new axes constraint that A is symmetic, 5) The volume is proportional tothe and it is positive de fi nite product of lengths of eigenvalues Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 4 / 42

Almost Every Problem can be posed as an Optimization Problem G i v e n a s e t C⊆ ℜ n find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat C⊆E . Hint: First work out the problem in lower dimensions Sphere S r ⊆ ℜ c e n t e r e d at 0 is e x p r e s s e d as: S r = { u ∈ ℜ n |∥ u ∥ 2 ≤ r } n Ellipsoid E⊆ ℜ n i s e x p r e s s e da s : { } { } , that is, A is E = v ∈ ℜ | A v + b ∈S = v ∈ ℜ|∥ A v + b ∥ ≤ 1 . Here, A ∈S n n n 1 2 ++ an n × n (strictly) p o s it iv e definite matrix. The optimization p r o b l e m willbe: m in im i z e det ( A − 1 ) [ a 11 , a 12 .., a nn , b 1 ,.. b n ] A is positive de fi nite T A v > 0 , ∀ v ̸ = 0 s u b j e c tto v C ∥ A v + b ∥ 2 ≤ 1 , ∀ v ∈C C is contained in the Ellipsoid Can forall v be changed to checking for a fi nite n u m b e r o f b o u n n T d B a m r b y ) points n ? P r o . G f a n e s hR a m a k i s r h n a ( I I o a y I t r o d u c t i o n to C o n v e x Optimization : CS709 July 17,2018 4 / 42

Almost Every Problem can be posed as an Optimization Problem (contd.) Give n a polygon P⊆ ℜ find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat n P ⊆ E . L e t v 1 , v 2 , ... v p b e t h e c o r n e r s of t h epolygon P The optimization p r o b l e m willbe: v1 m in im i z e det ( A − 1 ) v2 [ a 11 , a 12 .., a nn , b 1 ,.. b n ] s u b j e c tto − v T A v > 0 , ∀ v ̸ = 0 v3 ∥ A v + b ∥ 2 ≤ 1 , i ∈{ 1 .. p } v4 i v5 Given that the speci fi ed set S is indeed a polygon, is this problem with a simpli fi ed set of constraints equivalent to the original problem? Y E S P r o f . G a n e s hRamakrishnan (IIT Bombay) Introduction to C o n v e x Optimization: CS709 July 17, 2018 5 / 42

Almost Every Problem can be posed as an Optimization Problem (contd.) G i v e n a polygon P⊆ ℜ n find t h e ellipsoid E⊆ ℜ n that i s of s m a l l e s t v o l u m e s u c hthat P⊆E . L e t v 1 , v 2 , ... v p b e t h e c o r n e r s of t h e polygon P The optimization p r o b l e m willbe: m in im i z e det ( A − 1 ) [ a 11 , a 12 .., a nn , b 1 ,.. b n ] s u b j e c tto − v T A v > 0 , ∀ v ̸ = 0 ∥ A v i + b ∥ 2 ≤ 1 , i ∈{ 1 .. p } H o w w o u l d y o u p o s e a n optimization p r o b l e m to find t h e ellipsoid E ′ of l a r g e s t v o l u m e that fitsi n s i d e C ? Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 5 / 42

So Again: Mathematical optimization m i n i m i z e f 0 ( x ) x s u b j e c t to f i ( x ) ≤ b i , i = 1 , . . . , m . x = ( x 1 , ..., x n ) : optimizationv a r i a b l e s f i : ℜ n →ℜ , i = 1 , ..., m : c o n s t r a in tfu n c t io n s optimal solution x ∗ h a s s m a l l e s t v a l u e of f 0 a m o n g all v e c t o r s that s a t is fy t h ec o n s t r a i n t s Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 6 / 42

Examples portfolio optimization v a r ia b le s : a m o u n t s i n v e s t e d in differenta s s e t s c o n s t r a in t s : budget, max./min. i n v e s t m e n t p e r a s s e t ,m i n i m u m return o b je c t iv e : o v e r a ll r is k o r returnv a r i a n c e Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 7 / 42

Examples Data fitting - Machine learning v a r ia b le s : m o d e lp a r a m e t e r s c o n s t r a in t s : prior information, p a r a m e t e r limits o b je c t iv e : m e a s u r e of misfit o r p r e d ic t io ne r r o r Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 9 / 42

Applications S p a m De t e c t io n Digit Re c o g n it io n M e d ic a ld i a g n o s i s Bio-diversity c l a s s i f i c a t i o n Buying o r s e llin gp r o d u c t s Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 12 / 42

Problem in Perspective G i v e n d a t a points x i , i = 1 , 2 , . . . , m P o s s i b l e c l a s s c h o i c e s : c 1 , c 2 , . . . , c k Wish to g e n e r a t e amapping/classifier f : x → { c 1 , c 2 ,..., c k } T o g e t c l a s slabels y 1 , y 2 ,..., y m Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 13 / 42

Problem in Perspective In g e n e r a l, s e r i e s ofm a p p i n g s x f ( · ) g ( · h ( · ) ) −→ y −→ z −→{ c , c , . . ., c } 1 2 k eg: neural networks Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 14 / 42

Problem in Perspective In g e n e r a l, s e r i e s ofm a p p i n g s x f ( · ) g ( · h ( · ) ) −→ y −→ z −→{ c , c ,..., c } 1 2 k wh e re , z a r e in s o m e latents p a c e . y Prof. G a n e s h Ramakrishnan (IIT Bombay) Introduction to C o n v e x Optimization : CS709 July 17,2018 14 / 42