iii if
play

iii. if linear representation : : { symmetric { symmetric group - PowerPoint PPT Presentation

Sep 11, 2023 •165 likes •426 views

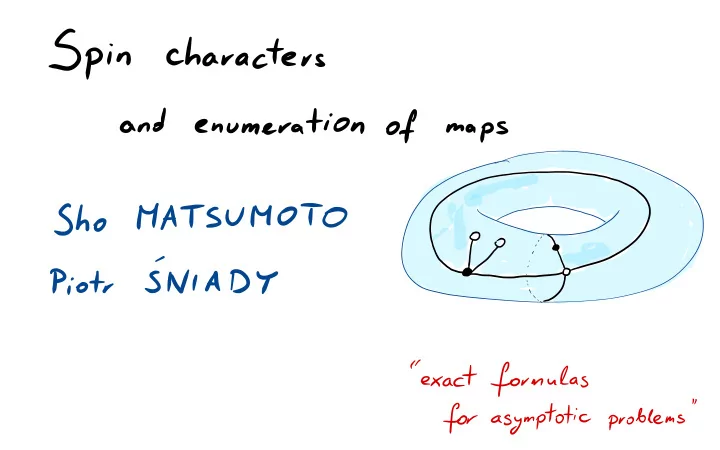
Spin characters and enumeration of maps " : :* : : " : " exact formulas " for asymptotic problems spin linear PCV ) V linear projective space - space - iii. if linear representation : :

  1. Spin characters and enumeration of maps " : :* : : " ÷ : " exact formulas " for asymptotic problems

  2. spin linear PCV ) V linear projective space - space - iii. if linear representation :÷÷÷÷÷÷÷÷÷ : { symmetric { symmetric group group of representations S projective . I linear representations of =

  3. Sn symmetric # group " " transpositions - simplex Cnn ) of symmetries ) .tn t - e . . . . . ite ) ti - Ci with , [ animated contents ] ) f . o - ( 2,3 ) ta transposition ti 1 - - I

  4. ~ 151=2 Sn n ! spin group t ) - simplex " ( rotations ER of double n of Sn - cover \ attache with ribbon , a generate ,¥yangp , , ↳ , , [ animated .tn tr # tents ] , . . . . l T €91800 I " ta - ( 2,3 ) " transposition " E. imam

  5. ~ 151=2 n ! Sn spin group - simplex t ) ( " ER rotations of double of Sn n - cover \ attache ribbon with , a generate , # gang , , , ↳ , , [ animated , tn tr # - y tents ] , . . . l # 360° l go ↳ § ti ! z = 360° twist the of ribbon z = at ¥..

  6. ↳ ~ 151=2 Sn n ! spin group t ) - simplex " ( rotations ER of double of Sn n - cover \ attache with ribbon , a generate , .gg [ clever , , , ↳ , ,p , , trick to , tn ten the - y untangle , . . . bbon ] . # €97200 a I 2 4 1 t z = = i , 2=360 twist the of ribbon µ imma

  7. - symmetric spin classes interesting conjugacy classes conjugacy I the Sn of symmetric the of group spin group indexed by indexed by are are in :÷÷¥ :* , " , " " IT Te = n t t It - - - Te = n , t . . .

  8. symmetric spin irreducible representations irreducible representations I of of Sn " almost :÷"÷÷÷ ! ! .es/sn*e.....w;..ngn...ag;;e by indexed a are , ¥¥ ¥ + An > He > se 5ns - - - . " , -

  9. " fix symmetric class spin conjugacy , function ate normalized irreducible on ~ Sn " Young " ! diagrams character Sn of O if nsk " Chi : = " chit |g ↳ ÷÷÷± ⇒⇒ it " . gym . . . . . . . . . . tht k " class tht k " " - jvgacy class - conjugacy odd partition

  10. alternative definition k for t odd partition it any Chin . ) FIX the sit function symmetric is unique : . . . . . . ] " F E[ F " E is • , Ps supersymmetric ps Pa . . , , 1512k Ffg ) O > for 5 . > ese - • - - - - F K and of degree is • [ homogeneous part ] - degree F pit top =

  11. alternative definition Littlewood Hall → - E- for -1 functions symmetric - functions ] P Schur → = ? X' fit ) Pg Pit \ MAGIC xena " . " as : = . . - 1- I > f- Young [ diagram n k " " I # k class conjugacy

  12. problem : ? - lest EE Nts les ) " Chi : , s %

  13. problem : ? - lest EE Nts les ) " Chi : , es graph on a surface

  14. ( 3) 6 ( 1,5 , 4,2 ) ( 2,82 ) of = permutations pair , - 34,5 ) V W 82=11,2 8 IT = , . 62=12,3 , 5) ( 1,4 ) n t YE G ) , @l.q.z bicolored graph g Q " I*7 " neater " ' ÷ :* . . - type with face it 17 torus >

  15. problem : " number of - colorings " Nts Z les ) chits , s %

  16. ↳ ⇒ - coloring ( frfr ) ( 8,82 ) ( 3 ) X 6 of ( 1,5 , 4,2 ) if is a = , T • f , 8 , columns to cycles of maps , fz ( 2 , 3,5 ) ( 1,4 ) cycles 82 of to • rows maps = , FF • tf 2. Q of C cycle Cz cycle of 82 - - . , - flat )e1 # 0 ( file . ) canoe > , iii :it *¥ ⇐ ¥÷ f. IV ) flw )

  17. ↳ ⇒ ( 3 ) 6 ( 1,5 , 4,2 ) - coloring of G ( f . ,fz ) X = is if a , T T • f , white vertices columns to maps , fz ( 2 , 3,5 ) ( 1,4 ) vertices black to • rows maps = , § • tf b white vertex black vertex w - - , , flat )e1 ( file b connected . ) w y , y " •••GZ iiiii :* . ¥i¥ . g - few ) f. ( w ) >

  18. symmetric ltl=k Stanley formula for partition it J diagram and Young " Chala ) -52 ( t ) th No . " . - Q , she Sk - colorings X number 9 of 8,8 . I - - ✓ ( 4,82 ) of IT identify partition " with permutation sum some over Sk oriented ITE maps - type " with face it

  19. spin symmetric 5 - ¥## fit s f- 1- diagram } 1=13/5 ) diagram Young shifted Young double

  20. spin Wtic - k lit Stanley formula for odd partition it f and shifted diagram Young " 1 . . . ( Dls ) ) spin Chile ) -52 No th z . - , ,8zE Sk G h ly number of Q8z=t Dlg ) - colorings - 14,82 ) of " sum over oriented maps orbits number of # - type connected with face " . .kz { n IT in under = . . . of components the map 44,8 , > action of

  21. two equivalent formulas PREVIOUS SLIDE : - # white #!, vertices n Dls ) ) citing ) -52 Ngl ta ) 2 components oriented with maps - type face IT NEW : - # white A T Z vertices n ) citing > Nixes ta ) - = zeal s oriented non - but orientable maps - type with face it

  22. 1 part proof " linear character Tht ( s ) f- Chit ( Dls ) ) define : = " to world exported spin # fun fact C- { 1. 3,5 . } a. b , c . . . . . . , symmetric spin Tha " Chs ! " to at = split most two " groups " .com : Chs : : Chs : CT + = . . " ? .ec " Tha Chinna Ch Ch + + . s a , . chat : ch : " " ' : ca Ch + + .

  23. 2 part proof - 15 . ( 2K - t ) ! ! f Mobius Hint invention use : : k = # blocks for " Cha China = Eh Tha Chi : Tha - - = . . . Eh Tha Ths Tha Chiari :c Tha = - - . . . . . . . . . Tha Tha Thr 3 Tha Ths t - , s apply now & cancellations formula Stanley symmetric magic , ]

  24. Homework better find proof : " n Neatness ) " th = ? ↳ " . 8^82=15 Chi " . ) Flx Hint the st symmetric function is unique : : . . . . . . ] " F E[ ✓ F " E • is , Ps ps supersymmetric pn . . , , 7 1512k Ffg ) O X > ese for 5 . > - . - - - . F K ✓ and of is degree • [ homogeneous part ] - degree F top pit =

  25. Application random Young shifted diagrams tableaux random shifted

  26. Summer School on Algebraic Combinatorics Cracow Poland . F ' , G July 2020 10 - , Valentin Ferry • Vic Reiner • • Anne Schilling psniady.impan.pl/ school

Recommend

More recommend